
Difeomorfisme
de clasa ![]() . Teorema functiilor implicite
. Teorema functiilor implicite
1. Definitie. Fie multimile deschise ![]() . Functia
. Functia ![]() se numeste difeomorfism de clasa
se numeste difeomorfism de clasa ![]() (sau
(sau ![]() difeomorfism) daca:
difeomorfism) daca:
(i)
. ![]() ;
;
(ii). ![]() este functie
bijectiva (exista inversa
este functie
bijectiva (exista inversa ![]() a.i.
a.i. ![]() si
si ![]() );
);
(iii). ![]() este de clasa
este de clasa ![]() pe
pe ![]() .
.
2. Observatie.
Orice difeomorfism de clasa ![]() este omeomorfism
(adica,
este omeomorfism
(adica, ![]() este functie continua;
este functie continua;
![]() functie
bijectiva;
functie
bijectiva; ![]() este functie
continua).
este functie
continua).
Reciproc nu este adevarat. De exemplu,
functia ![]() , definita prin
, definita prin ![]() ,
, ![]() este de clasa
este de clasa ![]() pe
pe ![]() , este bijectiva, dar functia inversa
, este bijectiva, dar functia inversa 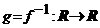 , definita prin
, definita prin ![]() , este continua pe
, este continua pe ![]() insa nu este de
clasa
insa nu este de
clasa ![]() pe
pe ![]() deoarece
deoarece ![]() nu este
diferentiabila in origine.
nu este
diferentiabila in origine.
Mai general, ![]() ,
, ![]() este omeomorfism, dar
nu este difeomorfism pe
este omeomorfism, dar
nu este difeomorfism pe ![]() .
.
Exemple: (1).
Fie ![]() este un punct fixat.
Functia
este un punct fixat.
Functia ![]() , definita prin
, definita prin ![]() (
(![]() defineste translatia
cu
defineste translatia
cu ![]() ,
, ![]() , pe axa reala). Atunci
, pe axa reala). Atunci ![]() este o izometrie (!) (se verifica
usor) si chiar difeomorfism
pe
este o izometrie (!) (se verifica
usor) si chiar difeomorfism
pe ![]() .
.
Intr-adevar, ![]() si functia
inversa,
si functia
inversa, ![]() , definita prin
, definita prin ![]() , sunt de clasa
, sunt de clasa ![]() .
.
. Fie ![]() este un vector fixat.
Functia vectoriala de variabila vectoriala
este un vector fixat.
Functia vectoriala de variabila vectoriala ![]() , definita prin
, definita prin ![]() , se numeste translatia
in spatiul vectorial
, se numeste translatia
in spatiul vectorial ![]() cu vectorul
cu vectorul ![]() ;
; ![]() este o izometrie (!) (se verifica
usor) si chiar difeomorfism
pe
este o izometrie (!) (se verifica
usor) si chiar difeomorfism
pe ![]() . In acest caz spunem ca
. In acest caz spunem ca ![]() realizeaza o transformare regulata (!) a
spatiului vectorial
realizeaza o transformare regulata (!) a
spatiului vectorial ![]() in el insusi.
in el insusi.
. Fie domeniile plane ![]() si
si ![]() (multimi deschise
si conexe). Aplicatia (functia)
(multimi deschise
si conexe). Aplicatia (functia) ![]() , definita prin
, definita prin ![]() , este un difeomorfism pe
, este un difeomorfism pe ![]() .
.
Intr-adevar, fie ![]() , unde
, unde ![]() si
si ![]() reprezinta functiile
componente ale lui
reprezinta functiile
componente ale lui ![]() . Atunci
. Atunci ![]() sunt de clasa
sunt de clasa ![]() exista
exista ![]() si
si ![]() si aceste
functii sunt continue pe
si aceste
functii sunt continue pe ![]() . Prin calcul direct, obtinem
. Prin calcul direct, obtinem ![]() si
si ![]() ,
, ![]() si deci,
si deci, ![]() . Observam ca functia
. Observam ca functia ![]() este bijectiva
si functia inversa
este bijectiva
si functia inversa ![]() este definita
prin
este definita
prin ![]() . Asadar,
. Asadar, ![]() si
si ![]() si cum suntem
interesati de restrictia lui
si cum suntem
interesati de restrictia lui ![]() la domeniul
la domeniul ![]() , atunci din
, atunci din ![]() obtinem
restrictia
obtinem
restrictia ![]() . In consecinta,
. In consecinta, ![]() si atunci
si atunci ![]() este o bijectie
si evident functia inversa
este o bijectie
si evident functia inversa ![]() este de clasa
este de clasa ![]() .
.
Exercitiul 1. Fie ![]() si
si ![]() multimi deschise
in
multimi deschise
in ![]() si
si ![]() si
si ![]() difeomorfisme. Atunci
difeomorfisme. Atunci ![]() este un difeomorfism
pe
este un difeomorfism
pe ![]() .
.
In continuare studiem posibilitatea derivarii aplicatiei
inverse a unei functii date (adica o generalizarea rezultatului de la
aplicatii de o singura variabila, ![]() ,
, ![]() bijectiva si
derivabila pe
bijectiva si
derivabila pe ![]() ).
).
3. Lema. Fie ![]() si
si ![]() doua spatii
euclidiene finit dimensionale si multimile deschise
doua spatii
euclidiene finit dimensionale si multimile deschise ![]() si
si ![]() si fie
si fie ![]() ,
, ![]() omeomorfism,
omeomorfism, ![]() diferentiabila intr-un punct
diferentiabila intr-un punct ![]() . Atunci proprietatile urmatoare sunt
echivalente:
. Atunci proprietatile urmatoare sunt
echivalente:
Functia ![]() este diferentiabila in
este diferentiabila in ![]() .
.
Aplicatia lineara ![]() este bijectiva,
este bijectiva, ![]() . Mai mult,
. Mai mult, ![]() .
.
4. Observatie.
In cazul functiilor de o variabila reala, ![]() , daca
, daca ![]() derivabila in
derivabila in ![]() si
si ![]() , atunci
, atunci ![]() si
si ![]() . (Lema 3 este o generalizare a acestui rezultat).
. (Lema 3 este o generalizare a acestui rezultat).
5. Observatie. Daca
alegem ![]() ,
,![]() , atunci din definitia omeomorfismului rezulta
, atunci din definitia omeomorfismului rezulta ![]() .
.
Demonstratie. "![]() ". Deoarece
". Deoarece ![]() omeomorfism atunci
omeomorfism atunci ![]() este functie
continua, bijectiva si functia inversa
este functie
continua, bijectiva si functia inversa ![]() este continua.
Avem
este continua.
Avem ![]() si
si ![]() si deoarece
si deoarece ![]() diferentiabila intr-un punct
diferentiabila intr-un punct ![]() , putem scrie (compunerile de aplicatii lineare)
, putem scrie (compunerile de aplicatii lineare)
![]() .
.
Cum ![]() este
diferentiabila in
este
diferentiabila in ![]() avem
avem
![]() .
.
Din aceste relatii deducem ca aplicatia ![]() este bijectiva,
avand inversa
este bijectiva,
avand inversa ![]() (vezi corolarul 9.27,
unde
(vezi corolarul 9.27,
unde ![]() ). In cazul functiilor de o variabila reala
avem
). In cazul functiilor de o variabila reala
avem ![]() .
.
"![]() ". Fie
". Fie ![]() ,
, ![]() aplicatie
bijectiva. Atunci cele doua spatii
aplicatie
bijectiva. Atunci cele doua spatii ![]() si
si ![]() au aceeasi
dimensiune si exista aplicatia inversa
au aceeasi
dimensiune si exista aplicatia inversa ![]() . Deoarece functia
. Deoarece functia ![]() este
diferentiabila in
este
diferentiabila in ![]() , atunci exista functia
, atunci exista functia ![]() ,
, ![]() continua in
continua in ![]() si
si ![]() a.i. sa avem
a.i. sa avem
![]() , pentru orice
, pentru orice ![]() . (16)
. (16)
Pentru a arata ca functia
inversa ![]() este
diferentiabila in
este
diferentiabila in ![]() , este suficient sa aratam ca
, este suficient sa aratam ca
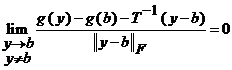 . (17)
. (17)
Daca notam cu ![]() atunci avem
atunci avem ![]() si relatia
(17) se scrie sub forma echivalenta
si relatia
(17) se scrie sub forma echivalenta
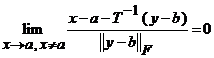 . (17')
. (17')
In relatia (16), scrisa sub forma ![]() , aplicam
, aplicam ![]() si obtinem
si obtinem
![]() , (*)
, (*)
de unde rezulta ![]() , care la norma se transforma in
, care la norma se transforma in
![]() .
.
Daca se trece la norma in (17') si se foloseste ultima relatie, atunci va trebui sa demonstram ca
![]() . (18)
. (18)
Trecand relatia (*) la norma avem
![]() ,
,
de unde deducem
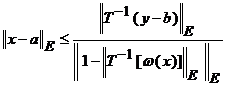 . (19)
. (19)
Folosind (19) cat si inegalitatea ![]() (renuntam la
indicele de norma), vom observa ca relatia (18) rezulta din
majorarile
(renuntam la
indicele de norma), vom observa ca relatia (18) rezulta din
majorarile
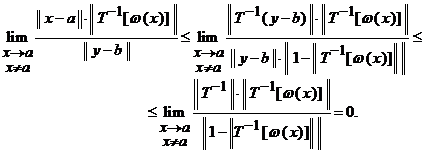 (20)
(20)
Pentru calculul limitei in (20) s-a folosit faptul
ca ![]() .
.
6. Teorema. (teorema
de caracterizare a difeomorfismelor) . Fie ![]() si
si ![]() doua multimi
deschise in spatiile euclidiene finit dimensionale
doua multimi
deschise in spatiile euclidiene finit dimensionale ![]() si respectiv
si respectiv ![]() si
si ![]() omeomorfism de
clasa
omeomorfism de
clasa ![]() . Atunci proprietatile urmatoare sunt echivalente:
. Atunci proprietatile urmatoare sunt echivalente:
Functia ![]() este
este ![]() difeomorfism pe
difeomorfism pe ![]() ;
;
Aplicatia inversa ![]() este
diferentiabila in orice punct din
este
diferentiabila in orice punct din ![]() ;
;
Aplicatia lineara ![]() , este bijectiva (deci,
, este bijectiva (deci, ![]() ),
), ![]() (adica, jacobianul
lui
(adica, jacobianul
lui ![]() este nenul,
este nenul, ![]() ).
).
7. Observatie.
Aplicatia lineara ![]() este bijectiva
este bijectiva ![]() matricea
matricea ![]() asociata lui
asociata lui ![]() (care corespunde la
doua baze fixate in
(care corespunde la
doua baze fixate in ![]() respectiv
respectiv ![]() ) este inversabila
) este inversabila ![]()
![]() .
.
Fie ![]() . Afirmatia "
. Afirmatia "![]() este bijectiva
" se poate exprima prin:
este bijectiva
" se poate exprima prin: ![]() este bijectiva
este bijectiva ![]() matricea jacobiana
matricea jacobiana
![]() asociata lui
asociata lui ![]() in orice
in orice ![]() este inversabila
este inversabila ![]() in orice punct
in orice punct![]() jacobialul lui
jacobialul lui ![]() ,
, ![]() .
.
Demonstratie. Implicatia "![]() " rezulta direct din definitie. Deci functia
" rezulta direct din definitie. Deci functia ![]() este
diferentiabila si aplicatia lineara
este
diferentiabila si aplicatia lineara ![]() este continua.
este continua.
![]() . Functia
. Functia ![]() fiind
diferentiabila peste tot in
fiind
diferentiabila peste tot in ![]() atunci
atunci ![]() exista unic
exista unic ![]() a.i.
a.i. ![]() este
diferentiabila
este
diferentiabila ![]() si potrivit lemei
3, rezulta ca
si potrivit lemei
3, rezulta ca ![]() este bijectiva
oricare ar fi
este bijectiva
oricare ar fi ![]() si
si ![]() cat si
cat si ![]() .
.
![]() . Din lema 3 rezulta ca
. Din lema 3 rezulta ca ![]() (care exista) este
diferentiabila in
(care exista) este
diferentiabila in ![]() . Deci, aplicatia
. Deci, aplicatia ![]() exista si vom
arata ca
exista si vom
arata ca ![]() este continua.
este continua.
Pentru a arata aceasta, fie ![]() , atunci
, atunci ![]() , unde functiile
, unde functiile ![]() sunt continue si atunci
jacobianul lui
sunt continue si atunci
jacobianul lui ![]() ,
, ![]() , este functie continua oricare ar fi
, este functie continua oricare ar fi ![]() . Aplicatia lineara asociata matricii
. Aplicatia lineara asociata matricii ![]() are forma
are forma
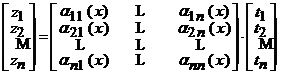 si
si 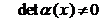 .
.
Asadar, matricea ![]() este inversabila
si putem scrie
este inversabila
si putem scrie 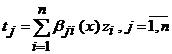 . Matricea
. Matricea
![]() este chiar
este chiar ![]() si aceasta se
calculeaza dupa relatii de forma
si aceasta se
calculeaza dupa relatii de forma
![]() ,
,
deci ![]() sunt functii
continue pe
sunt functii
continue pe ![]() .
.
Deoarece ![]() avem
avem ![]() . Deci,
. Deci, ![]() si avem
si avem ![]() este formata din
functii continue definite pe
este formata din
functii continue definite pe ![]() cu valori reale.
cu valori reale.
8. Definitie. Fie ![]() si
si ![]() . Functia
. Functia ![]() se numeste
se numeste ![]() difeomorfism local in
difeomorfism local in ![]() daca
exista o vecinatate
daca
exista o vecinatate ![]() si o
vecinatate
si o
vecinatate ![]() astfel incat
aplicatia
astfel incat
aplicatia ![]() sa fie
sa fie ![]() difeomorfism.
difeomorfism.
9. Observatie. (i). Orice difeomorfism local este omeomorfism local de spatii topologice.
(ii).
Daca ![]() este
este ![]() difeomorfism local in
difeomorfism local in ![]() atunci
atunci ![]() , unde
, unde ![]() si
si ![]() , iar aplicatia lineara
, iar aplicatia lineara![]() este bijectiva.
este bijectiva.
Exemplul (3) pune in evidenta dificultatile (uneori,
chiar imposibilitatea) de calcul al aplicatiei inverse si cu atat mai
mult posibilitatea de a arata ca ![]() este un difeomorfism.
Raspunsul la aceasta problema este dat de urmatoarea teorema
de caracterizare a
este un difeomorfism.
Raspunsul la aceasta problema este dat de urmatoarea teorema
de caracterizare a ![]() difeomorfismelor
locale:
difeomorfismelor
locale:
Teorema. (Teorema
de inversiune locala). Fie ![]() , functia
, functia ![]() si
si ![]() . Proprietatile urmatoare sunt echivalente:
. Proprietatile urmatoare sunt echivalente:
(1). Functia ![]() este
este ![]() difeomorfism local in
difeomorfism local in ![]() .
.
(2). Aplicatia lineara ![]() este bijectiva
(adica
este bijectiva
(adica ![]() ).
).
Altfel spus, daca ![]() multime
deschisa,
multime
deschisa, ![]() ,
, ![]() si
si ![]() atunci exista o
vecinatate
atunci exista o
vecinatate ![]() ,
, ![]() , este difeomorfism. Mai mult
, este difeomorfism. Mai mult ![]() si daca
si daca ![]() atunci
atunci ![]()
![]() .
.
Demonstratie. Analizam cazul ![]() . Implicatia "
. Implicatia "![]() " este evidenta.
" este evidenta.
"![]() ". Deoarece
". Deoarece ![]() atunci
atunci ![]() este continua pe
este continua pe ![]() si cum
si cum ![]() , putem presupune ca
, putem presupune ca ![]() . Asadar, exista o vecinatate
. Asadar, exista o vecinatate ![]() a. i.
a. i. ![]() . Atunci restrictia lui
. Atunci restrictia lui ![]() la
la ![]() , functia
, functia ![]() , este continua, crescatoare si in
consecinta, functia
, este continua, crescatoare si in
consecinta, functia ![]() este bijectiva.
este bijectiva.
Aratam ca functia
inversa ![]() este
diferentiabila pe
este
diferentiabila pe ![]() . Fie
. Fie ![]() oarecare, dar fixat si
unicul punct
oarecare, dar fixat si
unicul punct ![]() a.i.
a.i. ![]() . Atunci
. Atunci
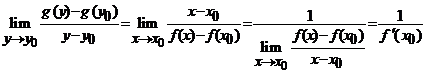
si deci ![]() . Cum
. Cum ![]() a fost ales oarecare,
rezulta ca aplicatia
a fost ales oarecare,
rezulta ca aplicatia ![]() , unde
, unde ![]() , este inversa aplicatiei
, este inversa aplicatiei ![]() si aceasta este
continua pe
si aceasta este
continua pe ![]() . Deoarece
. Deoarece ![]() este multime
deschisa,
este multime
deschisa, ![]() este continua
si cum
este continua
si cum ![]() rezulta ca
multimea
rezulta ca
multimea ![]() este o vecinatate
a lui
este o vecinatate
a lui ![]() .
.
11. Observatie. Aceasta implicatie rezulta direct din lema 3.
Functii implicite
Functiile definite cu ajutorul ecuatiilor (relatiilor) se numesc functii definite implicit, sau functii implicite.
(a). Cazul unei ecuatii care defineste implicit o functie de o variabila
Fie ecuatia
![]() ,
(1)
,
(1)
definita de functia de doua
variabile ![]() ,
, ![]() . Vom nota cu
. Vom nota cu ![]() proiectia
multimii
proiectia
multimii ![]() pe axa
pe axa ![]() ,
,
![]() si fie
si fie ![]() .
.
12.
Definitie. Functia
![]() ,
, 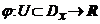 , se numeste solutie,
in raport cu
, se numeste solutie,
in raport cu ![]() , a ecuatiei
, a ecuatiei ![]() pe multimea
pe multimea ![]() daca si
numai daca
daca si
numai daca
![]() , oricare ar fi
, oricare ar fi ![]() . (2)
. (2)
13. Observatie. Asemanator ca mai sus, se pot defini
solutii in raport cu variabila ![]() . In general, o ecuatie
. In general, o ecuatie ![]() poate avea (in raport
cu una din variabile) una sau mai multe solutii pe o multime
poate avea (in raport
cu una din variabile) una sau mai multe solutii pe o multime ![]() sau nu poate avea
solutii pe acea multime.
sau nu poate avea
solutii pe acea multime.
Exemple:
. Fie functia ![]() , definita pe
, definita pe ![]() cu valori reale
si ecuatia
cu valori reale
si ecuatia ![]() , adica
, adica ![]() . Evident, ecuatia nu are solutii, in raport cu
. Evident, ecuatia nu are solutii, in raport cu ![]() , pentru orice
, pentru orice ![]() .
.
Fie
multimea ![]() . Aratam ca ecuatia
. Aratam ca ecuatia ![]() are in raport cu
are in raport cu ![]() o infinitate de
solutii pentru orice
o infinitate de
solutii pentru orice ![]() . Pentru aceasta este suficient sa consideram
multimile disjuncte
. Pentru aceasta este suficient sa consideram
multimile disjuncte ![]() si
si ![]() , astfel incat
, astfel incat ![]() . Pentru ca exista o infinitate de
posibilitati in alegerea multimilor
. Pentru ca exista o infinitate de
posibilitati in alegerea multimilor ![]() si
si ![]() , atunci exista o infinitate de moduri de a construi
functii
, atunci exista o infinitate de moduri de a construi
functii ![]() , definite prin
, definite prin
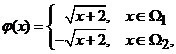
Deoarece se verifica identitatea ![]() pe
pe ![]() , atunci functia
, atunci functia ![]() este o solutie a
ecuatiei
este o solutie a
ecuatiei ![]() .
.
Este important sa retinem ca
dintre toate solutiile in raport cu ![]() ale ecuatiei
date, numai doua sunt definite
de functii continue pe
ale ecuatiei
date, numai doua sunt definite
de functii continue pe ![]() si anume
si anume
![]() si respectiv,
si respectiv, ![]() ,
, ![]() ;
;
iar, dintre aceste doua solutii
numai una si anume ![]() , verifica "conditia
initiala
, verifica "conditia
initiala ![]() ".
".
In acest ultim caz, cand exista o unica
functie care verifica ecuatia data si eventual
anumite conditii suplimentare spunem ca functia ![]() este definita de ecuatia
implicita
este definita de ecuatia
implicita ![]() .
.
. Functia ![]() cu
cu ![]() , defineste ecuatia
, defineste ecuatia ![]() . Este usor de vazut ca aceasta
ecuatie nu are solutii reale nici in raport cu
. Este usor de vazut ca aceasta
ecuatie nu are solutii reale nici in raport cu ![]() nici in raport cu
nici in raport cu ![]() .
.
. Ecuatia ![]() ,
, ![]() are o unica solutie in raport cu
are o unica solutie in raport cu ![]() , pentru orice
, pentru orice ![]() si anume functia
si anume functia
![]() ; evident, aceasta ecuatie are o unica solutie in raport cu
; evident, aceasta ecuatie are o unica solutie in raport cu ![]() , pentru orice
, pentru orice ![]() si anume
functia
si anume
functia ![]() .
.
b). Cazul unei ecuatii care defineste implicit o functie de mai multe variabile.
Consideram ecuatia
![]() , (3)
, (3)
definita de functia ![]() .
.
14.
Definitie. O
functie de ![]() -variabile
-variabile ![]() ,
, ![]() se numeste solutie in raport cu
se numeste solutie in raport cu ![]() a ecuatiei (3),
pe multimea
a ecuatiei (3),
pe multimea ![]() , daca
, daca
![]() oricare ar fi
oricare ar fi ![]() . (4)
. (4)
Vom observa ca daca folosim
notatia ![]() atunci ecuatia (3)
poate fi scrisa sub forma
atunci ecuatia (3)
poate fi scrisa sub forma ![]() , iar solutia
, iar solutia ![]() se scrie
se scrie ![]() .
.
Asadar, putem considera numai
ecuatii de forma ![]() , unde
, unde ![]() este o variabila
reala sau vectoriala.
este o variabila
reala sau vectoriala.
Daca exista o unica
functie ![]() care verifica
ecuatia data si eventual anumite conditii suplimentare spunem ca aceasta functie
este definita implicit de ecuatia
care verifica
ecuatia data si eventual anumite conditii suplimentare spunem ca aceasta functie
este definita implicit de ecuatia ![]() , sau ca prin
rezolvarea ecuatiei
, sau ca prin
rezolvarea ecuatiei ![]() in raport cu
in raport cu ![]() , obtinem o unica functie
, obtinem o unica functie ![]() .
.
Conditii suficiente de existenta functiilor implicite.
15.
Propozitie. Fie
functia ![]() ,
, ![]() , unde
, unde ![]() este o multime
deschisa care contine punctul
interior
este o multime
deschisa care contine punctul
interior ![]() .
.
Daca se verifica conditiile:
1). ![]() ;
;
2). exista o vecinatate ![]() in
in ![]() si o
vecinatate
si o
vecinatate ![]() in
in ![]() , a.i. punctul
, a.i. punctul ![]() si pentru orice
si pentru orice ![]() fixat, functia
fixat, functia ![]() (privita ca
functie de
(privita ca
functie de ![]() ) este continua si strict monotona pe
) este continua si strict monotona pe ![]() ;
;
3). pentru orice ![]() fixat, functia
fixat, functia ![]() (privita ca
functie de variabila vectoriala
(privita ca
functie de variabila vectoriala ![]() ) este continua in
) este continua in ![]() ;
;
atunci exista o vecinatate ![]() si o
vecinatate
si o
vecinatate ![]() , a.i.
, a.i. ![]() si o unica
functie implicita
si o unica
functie implicita ![]() , continua in
, continua in ![]() , care verifica egalitatea
, care verifica egalitatea ![]() si astfel incat
si astfel incat
![]() oricare ar fi
oricare ar fi ![]() .
.
16. Observatie.
Propozitia afirma ca daca se verifica ecuatia ![]() , atunci pentru
, atunci pentru ![]() apartinand unei
anumite vecinatati a lui
apartinand unei
anumite vecinatati a lui ![]() , ecuatia
, ecuatia ![]() are o unica solutie, adica din
ecuatia
are o unica solutie, adica din
ecuatia ![]() putem determina
implicit pe
putem determina
implicit pe ![]() ca functie de
ca functie de ![]() , de forma
, de forma ![]() .
.
Demonstratie. Alegem ![]() a.i.
a.i. ![]() si notam
si notam ![]() . Functia
. Functia ![]() , ca functie de variabila reala
, ca functie de variabila reala ![]() este strict
monotona pe
este strict
monotona pe ![]() . Deoarece
. Deoarece ![]() cu
cu ![]() , deducem ca functia
, deducem ca functia ![]() are semne diferite in
are semne diferite in ![]() si
si ![]() . Pentru a fixa ideile, sa presupunem ca
. Pentru a fixa ideile, sa presupunem ca ![]() si
si ![]() . Datorita ipotezei 3), functia
. Datorita ipotezei 3), functia ![]() este continua in
este continua in ![]() si deoarece avem
si deoarece avem ![]() , atunci exista o vecinatate
, atunci exista o vecinatate ![]() a lui
a lui ![]() astfel incat
astfel incat ![]() pentru orice
pentru orice ![]() . Un rationament asemanator ne conduce la
concluzia ca exista o vecinatate
. Un rationament asemanator ne conduce la
concluzia ca exista o vecinatate ![]() a lui
a lui ![]() astfel incat
astfel incat ![]() pentru orice
pentru orice ![]() . Daca notam
. Daca notam ![]() , atunci
, atunci ![]() este o vecinatate
a lui
este o vecinatate
a lui ![]() si avem
si avem ![]() pentru orice
pentru orice ![]() .
.
Fie ![]() un punct oarecare, dar
fixat. Datorita ipotezei 2), functia
un punct oarecare, dar
fixat. Datorita ipotezei 2), functia ![]() , privita ca functie de variabila
, privita ca functie de variabila ![]() , este continua si monotona pe
, este continua si monotona pe ![]() . Din continuitate deducem ca are proprietatea lui
Darboux, iar din inegalitatile
. Din continuitate deducem ca are proprietatea lui
Darboux, iar din inegalitatile ![]() si
si ![]() rezulta ca
exista un unic punct
rezulta ca
exista un unic punct ![]() astfel incat
astfel incat ![]() . Deoarece
. Deoarece ![]() a fost ales arbitrar,
rezulta ca pentru orice
a fost ales arbitrar,
rezulta ca pentru orice ![]() fixat, exista un
unic punct (!)
fixat, exista un
unic punct (!) ![]() , astfel incat
, astfel incat ![]() . Pentru
. Pentru ![]() , avem
, avem ![]() si cum
si cum ![]() este unicul punct cu
aceasta proprietate, deducem ca
este unicul punct cu
aceasta proprietate, deducem ca ![]() .
.
Aratam ca
functia ![]() este continua in
este continua in ![]() . Pentru aceasta, vom observa ca vecinatatea
. Pentru aceasta, vom observa ca vecinatatea ![]() a fost aleasa
arbitrar si din cele aratate mai inainte rezulta ca pentru
orice vecinatate
a fost aleasa
arbitrar si din cele aratate mai inainte rezulta ca pentru
orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() , astfel incat pentru orice
, astfel incat pentru orice ![]() sa avem
sa avem ![]() . Deci functia
. Deci functia ![]() este continua in
este continua in ![]() .
.
17. Observatie. Daca in locul ipotezei 3) din propozitia
15, cerem ca pentru orice ![]() fixat, functia
fixat, functia ![]() (privita ca
functie de variabila vectoriala
(privita ca
functie de variabila vectoriala ![]() ) sa fie continua pe
) sa fie continua pe ![]() (nu numai in punctul
(nu numai in punctul ![]() ), atunci functia implicita
), atunci functia implicita ![]() este continua pe
este continua pe ![]() .
.
18.
Teorema functiilor implicite. Fie ![]() o multime
deschisa care contine punctul
interior
o multime
deschisa care contine punctul
interior ![]() si functia
si functia ![]() , care verifica
conditiile:
, care verifica
conditiile:
1) ![]() ;
;
2) functia ![]() are toate derivatele
partiale,
are toate derivatele
partiale, ![]() continue in
continue in ![]() , deci acestea sunt continue intr-o vecinatate a
punctului
, deci acestea sunt continue intr-o vecinatate a
punctului ![]() ;
;
3) ![]() ;
;
atunci exista o vecinatate ![]() a lui
a lui ![]() si o
vecinatate
si o
vecinatate ![]() a lui
a lui ![]() si o unica functie
si o unica functie ![]() astfel incat
astfel incat
![]() si
si ![]() pentru orice
pentru orice ![]() ;
;
Mai mult, vecinatatile ![]() si
si ![]() pot fi alese astfel
incat functia
pot fi alese astfel
incat functia ![]() sa fie de
clasa
sa fie de
clasa ![]() si
si ![]() oricare ar fi
oricare ar fi ![]() si pentru orice
indice
si pentru orice
indice ![]() sa avem
sa avem
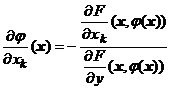 , oricare ar fi
, oricare ar fi ![]() . (5)
. (5)
19. Observatie.
Teorema afirma ca daca se verifica ecuatia ![]() , atunci pentru orice
, atunci pentru orice ![]() apartinand unei
anumite vecinatati a lui
apartinand unei
anumite vecinatati a lui ![]() , ecuatia
, ecuatia ![]() are o unica solutie adica, din
ecuatia
are o unica solutie adica, din
ecuatia ![]() putem determina
explicit pe
putem determina
explicit pe ![]() ca functie de
ca functie de ![]() ,
, ![]() ; in plus, datorita ipotezelor impuse,
; in plus, datorita ipotezelor impuse, ![]() si derivatele
partiale ale functiei
si derivatele
partiale ale functiei ![]() sunt date de
relatiile (5).
sunt date de
relatiile (5).
Demonstratie. Deoarece ![]() este functie
continua si nenula in
este functie
continua si nenula in ![]() , atunci exista o intreaga vecinatate
, atunci exista o intreaga vecinatate ![]() astfel incat
astfel incat ![]() , oricare ar fi
, oricare ar fi ![]() . Din ipoteza 2) rezulta ca functia
. Din ipoteza 2) rezulta ca functia ![]() este
diferentiabila in
este
diferentiabila in ![]() , deci continua in acest punct. Asadar, putem alege
vecinatatea
, deci continua in acest punct. Asadar, putem alege
vecinatatea ![]() a.i. functia
a.i. functia ![]() sa fie
continua pe
sa fie
continua pe ![]() . In particular, pentru orice
. In particular, pentru orice ![]() fixat, functia
fixat, functia ![]() este continua in
este continua in ![]() (se poate arata ca
este continua chiar pe
(se poate arata ca
este continua chiar pe ![]() ).
).
Fie ![]() fixat. Atunci
functia
fixat. Atunci
functia ![]() , ca functie de variabila
, ca functie de variabila ![]() , are derivata nenula pe
, are derivata nenula pe ![]() , deci este strict monotona pe
, deci este strict monotona pe ![]() . Asadar, ipotezele propozitiei 3 sunt verificate
si atunci exista o unica
functie
. Asadar, ipotezele propozitiei 3 sunt verificate
si atunci exista o unica
functie ![]() a. i.
a. i. ![]() si
si ![]() pentru orice
pentru orice ![]() .
.
Pentru a arata ca functia ![]() are derivatele
partiale continue pe
are derivatele
partiale continue pe ![]() vom arata mai
intai ca functia
vom arata mai
intai ca functia ![]() este
diferentiabila pe
este
diferentiabila pe ![]() . Fie
. Fie ![]() si
si ![]() . Deoarece functia
. Deoarece functia ![]() este
diferentiabila pe
este
diferentiabila pe ![]() atunci exista
functiile
atunci exista
functiile ![]() si
si ![]() continue, astfel incat
continue, astfel incat
![]() si
si ![]() si putem scrie
relatia
si putem scrie
relatia
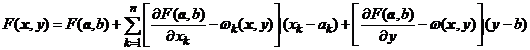 .
.
In particular, pentru ![]() si
si ![]() de forma
de forma ![]() , atunci
, atunci ![]() si
si ![]() si egalitatea
precedenta devine
si egalitatea
precedenta devine
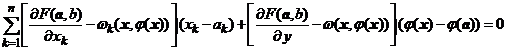 . (*)
. (*)
Cum functia ![]() este continua in
este continua in ![]() si functiile
si functiile
![]() si
si ![]() sunt continue in
sunt continue in ![]() , deducem ca functiile compuse
, deducem ca functiile compuse ![]() si
si ![]() sunt continue in
sunt continue in ![]() si
si
![]() ;
; ![]() .
.
Deoarece 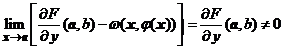 , atunci exista o vecinatate
, atunci exista o vecinatate ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() sa avem
sa avem ![]() . Din egalitatea (*) rezulta
. Din egalitatea (*) rezulta
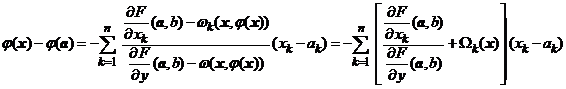 ,
,
unde 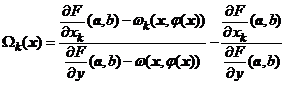 . Deoarece
. Deoarece ![]() rezulta ca
functia
rezulta ca
functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() si are derivatele
partiale continue in
si are derivatele
partiale continue in ![]() definite de
relatiile
definite de
relatiile
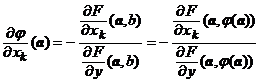 .
.
Deoarece, punctul ![]() a fost ales arbitrar
in
a fost ales arbitrar
in ![]() , rezulta ca functia
, rezulta ca functia ![]() este
diferentiabila in orice punct
este
diferentiabila in orice punct ![]() si derivatele
sale partiale sunt date de relatiile (5).
si derivatele
sale partiale sunt date de relatiile (5).
20. Observatie.
Daca functia ![]() este de clasa
este de clasa ![]() , atunci functia implicita
, atunci functia implicita ![]() este de clasa
este de clasa ![]() si derivatele
sale partiale de ordin superior se construiesc recurent.
si derivatele
sale partiale de ordin superior se construiesc recurent.
Exemple
Ecuatia
![]() , defineste implicit functia
, defineste implicit functia ![]() . Sa se calculeze derivatele
. Sa se calculeze derivatele ![]() si
si ![]() , stiind ca
, stiind ca ![]() .
.
Solutie. Fie functia ![]() . Functia implicita
. Functia implicita ![]() exista intr-o
vecinatate punctelor cu proprietatea
exista intr-o
vecinatate punctelor cu proprietatea ![]() , altfel spus, in punctele
, altfel spus, in punctele ![]() pentru care
pentru care ![]() . Cu aceasta presupunere putem scrie:
. Cu aceasta presupunere putem scrie:
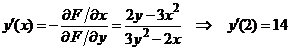 .
.
Reamintim ca pentru calculul derivatei a
doua, va trebui sa folosim in expresia primei derivate faptul ca ![]() este functie de
este functie de ![]() , adica
, adica
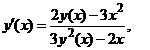 apoi vom deriva ca raport de functii. Avem
apoi vom deriva ca raport de functii. Avem
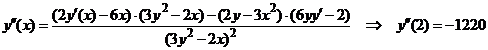 .
.
Ecuatia
![]() , unde
, unde ![]() , defineste implicit functia
, defineste implicit functia ![]() . Calculati
. Calculati ![]() si
si ![]() .
.
Solutie. Functia implicita ![]() exista in
vecinatatea punctelor din
exista in
vecinatatea punctelor din ![]() cu proprietatea
cu proprietatea ![]() , adica
, adica ![]() . De exemplu,
. De exemplu, ![]() poate fi un astfel de
punct. In aceasta ipoteza sunt indeplinite cerintele teoremei
functiilor implicite si atunci se pot calcula derivatele partiale
ale functiei
poate fi un astfel de
punct. In aceasta ipoteza sunt indeplinite cerintele teoremei
functiilor implicite si atunci se pot calcula derivatele partiale
ale functiei ![]() , derivand relatia
, derivand relatia ![]() in raport cu
in raport cu ![]() respectiv cu
respectiv cu ![]() . Avem
. Avem
![]() ,
,
de unde obtinem ![]() .
.
![]() ,
,
de unde se obtine![]() .
.
Vom
observa ca putem aplica direct formulele (5) si evident, obtinem
aceleasi relatii intr-o vecinatate a punctului ![]() :
:
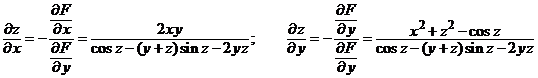 .
.
21. Teorema functiilor implicite (Cazul
general). Fie ![]() o multime deschisa si
o multime deschisa si ![]() si
si ![]() ,
, ![]() , o functie de clasa
, o functie de clasa ![]() astfel incat sa se
verifice conditiile:
astfel incat sa se
verifice conditiile:
(1) ![]() ;
;
(2) 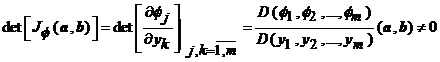 ,
,
atunci
exista o unica aplicatie ![]() definita pe o
vecinatate deschisa convenabila
definita pe o
vecinatate deschisa convenabila ![]() ,
, ![]() ,
, ![]() de clasa
de clasa ![]() a.i.
a.i. ![]() si
restrictia lui
si
restrictia lui ![]() la multimea
la multimea ![]() ,
,![]() , verifica ecuatia
, verifica ecuatia ![]() , oricare ar fi
, oricare ar fi ![]() .
.
22. Observatie.
Teorema afirma ca daca ecuatia ![]() , atunci intr-o vecinatate
, atunci intr-o vecinatate ![]() , ecuatia
, ecuatia ![]() determina
implicit pe
determina
implicit pe ![]() ca functie de
ca functie de ![]() ,
, ![]() .
.
Demonstratie. Consideram functia ![]() , definita astfel:
, definita astfel:
![]() ,
, ![]() ,
, ![]() .
.
Atunci ecuatia ![]() , unde
, unde ![]() ,
, ![]() , se scrie:
, se scrie:
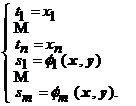 si avem
si avem 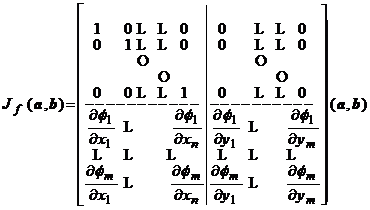
de
unde deducem ca 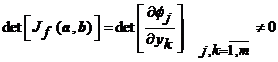 .
.
Asadar, aplicatia lineara ![]() este bijectiva
si potrivit teoremei de inversiune locala rezulta ca
este bijectiva
si potrivit teoremei de inversiune locala rezulta ca ![]() este un
este un ![]() difeomorfism local in
difeomorfism local in ![]() .
.
Cum ![]() atunci, din teorema de
inversiune locala, rezulta ca exista vecinatatea
atunci, din teorema de
inversiune locala, rezulta ca exista vecinatatea ![]() in
in ![]() si
vecinatatea
si
vecinatatea ![]() in
in ![]() astfel ca
astfel ca ![]() si a.i.
si a.i. ![]() sa fie
sa fie ![]() difeomorfism.
difeomorfism.
Fie functia ![]() aplicatia
inversa a lui
aplicatia
inversa a lui ![]() . Deoarece exista
. Deoarece exista ![]() in
in ![]() astfel incat
astfel incat ![]() , atunci
, atunci ![]() este de clasa
este de clasa ![]() . Functia
. Functia ![]() ,
, ![]() , definita prin componentele sale
, definita prin componentele sale ![]() ,
, ![]() , este functia cautata.
, este functia cautata.
Transformari
punctuale in spatiul euclidian ![]()
Consideram multimea deschisa ![]() . Fie functiile
. Fie functiile ![]() care fac sa
corespunda punctului
care fac sa
corespunda punctului ![]() un punct
un punct ![]() situat intr-un anumit
domeniu
situat intr-un anumit
domeniu ![]() , notate
, notate
![]() (1)
(1)
|
Figura 1.Transformare punctuala in plan. |
Functia ![]() de variabile
vectoriale cu valori vectoriale definita prin
de variabile
vectoriale cu valori vectoriale definita prin
![]() , (3.2)
, (3.2)
care asociaza la orice punct ![]() un unic punct
un unic punct ![]() se numeste transformare punctuala.
Functiile
se numeste transformare punctuala.
Functiile ![]() si
si ![]() se numesc componentele reale ale
transformarii punctuale
se numesc componentele reale ale
transformarii punctuale![]() .
.
Un interes deosebit il reprezinta transformarile biunivoce care apartin unei amumite clase de netezime.
23.
Definitie. Functia
![]() se numeste difeomorfism
de clasa
se numeste difeomorfism
de clasa ![]() (sau
(sau ![]() difeomorfism pe
difeomorfism pe ![]() ) daca sunt verificate conditiile:
) daca sunt verificate conditiile:
(1) ![]() ;
;
(2) ![]() este aplicatie
bijectiva de la
este aplicatie
bijectiva de la ![]() la
la ![]() (exista
functia inversa
(exista
functia inversa ![]() );
);
functia inversa notata ![]() este de clasa
este de clasa ![]() .
.
Din definitie rezulta ca orice difeomorfism ![]() de clasa
de clasa ![]() este omeomorfism pe
este omeomorfism pe ![]() .
.
(Reamintim ca functia ![]() se numeste omeomorfism pe
se numeste omeomorfism pe ![]() daca
verifica proprietatile:
daca
verifica proprietatile: ![]() este functie
continua pe
este functie
continua pe ![]() ;
; ![]() este bijectiva; functia inversa
este bijectiva; functia inversa ![]() este continua pe
este continua pe ![]() ).
).
24.
Definitie. Fie ![]() o multime
deschisa din
o multime
deschisa din ![]() . Functia vectoriala
. Functia vectoriala ![]() se numeste transformare regulata in punctul
se numeste transformare regulata in punctul ![]() , daca si numai daca sunt verificate
conditiile:
, daca si numai daca sunt verificate
conditiile:
exista o vecinatate ![]() ,
, ![]() a.i. functiile
a.i. functiile ![]() sunt derivabile
si au derivatele partiale continue pe
sunt derivabile
si au derivatele partiale continue pe ![]() (adica,
(adica, ![]() );
);
Determinantul functional
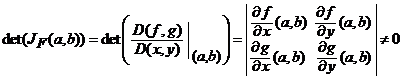 .
.
Altfel spus, functia vectoriala ![]() este transformare regulata in punctul
este transformare regulata in punctul ![]() , daca si numai daca exista o vecinatate
, daca si numai daca exista o vecinatate
![]() ,
, ![]() a.i. restrictia
lui
a.i. restrictia
lui ![]() la
la ![]() ,
, ![]() , defineste un difeomorfism pe
, defineste un difeomorfism pe ![]() (vezi teorema 10).
(vezi teorema 10).
Transformata ![]() se numeste
transformata regulata pe
se numeste
transformata regulata pe ![]() daca este
transformata regulata in orice punct
daca este
transformata regulata in orice punct ![]() .
.
Vom observa ca daca ![]() este transformare
regulata in punctul
este transformare
regulata in punctul ![]() , atunci
, atunci ![]() este transformare
regulata intr-o intreaga vecinatate a punctului
este transformare
regulata intr-o intreaga vecinatate a punctului ![]() . Intr-adevar, deoarece
. Intr-adevar, deoarece ![]() intr-o vecinatate
intr-o vecinatate
![]() a punctului
a punctului ![]() , atunci jacobianul este functie continua in
, atunci jacobianul este functie continua in ![]() si diferit de
zero in acest punct; deci exista o vecinatate
si diferit de
zero in acest punct; deci exista o vecinatate ![]() a punctului
a punctului ![]() pe care jacobianul
este nenul in vecinatatea
pe care jacobianul
este nenul in vecinatatea ![]() a lui
a lui ![]() . Asadar, in vecinatatea
. Asadar, in vecinatatea ![]() avem
avem ![]() si jacobianul
este nenul, deci
si jacobianul
este nenul, deci ![]() este transformare
regulata in
este transformare
regulata in ![]() .
.
25.
Propozitie. Jacobianul
unei transformari regulate in domeniul ![]() pastreaza
acelasi semn in orice punct
pastreaza
acelasi semn in orice punct ![]() .
.
Demonstratie. Deoarece transformarea este regulata
pe domeniul ![]() (multime conexa si deschisa), atunci jacobianul transformarii este
functie continua pe
(multime conexa si deschisa), atunci jacobianul transformarii este
functie continua pe ![]() . Daca jacobianul ar lua valori de semne diferite in
doua puncte distincte din
. Daca jacobianul ar lua valori de semne diferite in
doua puncte distincte din ![]() , atunci exista un punct
, atunci exista un punct ![]() a.i.
a.i. ![]() ceea ce ar contrazice
ipoteza ca transformarea este regulata in
ceea ce ar contrazice
ipoteza ca transformarea este regulata in ![]() .
.
Exemplul
1. Fie ![]() si functiile
si functiile
![]()
![]()
![]()
Vom arata ca relatiile ![]() asociaza la orice
punct
asociaza la orice
punct ![]() un unic punct
un unic punct ![]() unde
unde ![]() .
.
(i) Multimea ![]() este inchisa
si marginita. Daca
este inchisa
si marginita. Daca ![]() este frontiera
domeniului
este frontiera
domeniului ![]() (vezi fig. 2), atunci
(vezi fig. 2), atunci ![]() . Analog, definim
. Analog, definim ![]() , unde cu
, unde cu ![]() s-a notat frontiera
domeniului
s-a notat frontiera
domeniului ![]() ; Frontierele
; Frontierele ![]() si
si ![]() sunt curbe plane
simple inchise evident, considerate cu orientarile lor. Definim
functia
sunt curbe plane
simple inchise evident, considerate cu orientarile lor. Definim
functia ![]() . Se verifica usor ca
. Se verifica usor ca ![]() .
.
|
Figura 2. |
(ii) Jacobianul transformarii ![]() este nenul in fiecare
punct din
este nenul in fiecare
punct din ![]() :
:
![]() .
.
Atunci functia ![]() duce frontiera
duce frontiera ![]() a domeniului
a domeniului ![]() in frontiera
in frontiera ![]() a domeniului
a domeniului ![]() si deoarece
jacobianul este negativ, atunci transformarea
si deoarece
jacobianul este negativ, atunci transformarea ![]() schimba
orientarile acestor frontiere. Cum jacobianul este nenul pe
schimba
orientarile acestor frontiere. Cum jacobianul este nenul pe ![]() , atunci functia
, atunci functia ![]() realizeaza o transformare regulata a domeniului
realizeaza o transformare regulata a domeniului ![]() in domeniul
in domeniul ![]() .
.
Inversa transformarii ![]() ,
, ![]() , are forma
, are forma
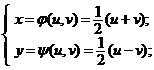
si jacobianul transformarii inverse are valoarea
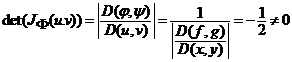 , in orice punct din
, in orice punct din ![]() .
.
Exemplul 2. Transformarea de coordonate polare in plan (vezi Fig. 3)
![]() ,
, ![]() ,
, ![]()
defineste functia vectoriala ![]() ,
, ![]() , care are jacobianul
, care are jacobianul ![]() . Se observa ca jacobianul acestei
transformari este nenul in toate punctele din spatiul euclidian
bidimensional cu exceptia originii. Se verifica direct ca
transformarea
. Se observa ca jacobianul acestei
transformari este nenul in toate punctele din spatiul euclidian
bidimensional cu exceptia originii. Se verifica direct ca
transformarea ![]() este este
regulata pe multimea deschisa si conexa
este este
regulata pe multimea deschisa si conexa ![]() .
.
Transformarea inversa, ![]() , definita de functiile coordonate
, definita de functiile coordonate
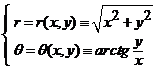 , oricare ar fi
, oricare ar fi ![]() ,
, ![]()
se scrie ![]() . Functia
. Functia ![]() este de clasa
este de clasa ![]() pe
pe ![]() si avem
si avem
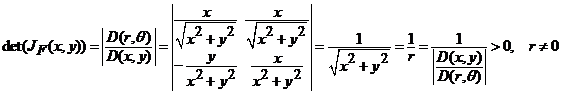 .
.
Functia ![]() , definita de relatiile
, definita de relatiile ![]() , deoarece are jacobianul pozitiv pentru
, deoarece are jacobianul pozitiv pentru ![]() realizeaza o
transformare regulata a domeniului
realizeaza o
transformare regulata a domeniului ![]() pe domeniul
pe domeniul ![]() .
.
26. Observatie. Transformarea poate fi considerata regulata in tot planul; originea este punct de neregularitate impus de alegerea coordonatelor polare.
|
Figura3. |
Dependenta si independenta functionala
27. Fie ![]() o multime deschisa si
o multime deschisa si
![]() ,
, ![]() (1)
(1)
un sistem de ![]() (
(![]() ) functii reale care depind de
) functii reale care depind de ![]() variabile independente
variabile independente
![]() . Presupunem ca functiile
. Presupunem ca functiile ![]() sunt de clasa
sunt de clasa ![]() pe
pe ![]() .
.
28.
Definitie. Sistemul de
functii ![]() se numeste functional dependent pe
se numeste functional dependent pe ![]() (sau functiile
(sau functiile ![]() sunt dependente functional pe
sunt dependente functional pe ![]() ) daca cel putin valoarea uneia dintre aceste
functii, sa zicem,
) daca cel putin valoarea uneia dintre aceste
functii, sa zicem, ![]() , se poate exprima unic
in
, se poate exprima unic
in ![]() ca "functie" de
valorile celorlalte functii,
ca "functie" de
valorile celorlalte functii, ![]() ;
;
Altfel spus, sa existe o functie ![]() , definita prin relatia
, definita prin relatia
![]() , (2)
, (2)
astfel incat relatia (1.2) se transforma in identitate in
raport cu ![]() din
din ![]() daca inlocuim
daca inlocuim ![]() ,
, ![]() ; adica se verifica relatia
; adica se verifica relatia
![]() oricare ar fi
oricare ar fi ![]() . (2')
. (2')
Daca relatia (2) este
verificata (sau (2')) atunci spunem ca functia ![]() este dependenta functional de
functiile
este dependenta functional de
functiile ![]() , pe multimea deschisa
, pe multimea deschisa ![]() .
.
Daca in ![]() , sau in nici o submultime din
, sau in nici o submultime din ![]() , nu are loc o identitate de tipul (2) atunci functiile
sistemului (1) se numesc independente
in
, nu are loc o identitate de tipul (2) atunci functiile
sistemului (1) se numesc independente
in ![]() .
.
29. Observatie.
(a). Daca, in particular,
functia ![]() se reduce la o
constanta, atunci evident ea depinde de celelalte functii si
scriem
se reduce la o
constanta, atunci evident ea depinde de celelalte functii si
scriem ![]() .
.
(b).
Dependenta functionala se refera la faptul ca una
dintre functii se exprima ca functie de celelalte functii
si aceasta notiune este o generalizare a dependentei
lineare; sistemul de functii ![]() este linear dependent pe
este linear dependent pe ![]() daca si
numai daca exista numerele reale
daca si
numai daca exista numerele reale ![]() , nu toate nule, sa zicem
, nu toate nule, sa zicem ![]() , a.i.
, a.i.
![]() , (3)
, (3)
unde "![]() " este functia identic nula (adica,
" este functia identic nula (adica, ![]() ), sau echivalent,
), sau echivalent,
![]() . (3')
. (3')
Daca impartim cu ![]() in (1.3') obtinem
in (1.3') obtinem
![]() , (3")
, (3")
care exprima, evident, dependenta
functionala a functiei ![]() de functiile
de functiile ![]() .
.
Exemplul 1. Fie
![]() ,
,
unde ![]() .
.
Se verifica usor ca in intreg
spatiu ![]() are loc relatia
are loc relatia ![]() . Asadar, daca definim
. Asadar, daca definim ![]() , prin
, prin ![]() , atunci obtinem
, atunci obtinem ![]() sau
sau
![]() .
.
Deci functiile ![]() sunt functional
dependente in
sunt functional
dependente in ![]() .
.
In multe cazuri este foarte dificil de stabilit o relatie functionala intre functiile unui sistem dat, evident daca o astfel de relatie exista.
Rezolvarea problemei dependentei sau independentei functionale a sistemului de functii (1) conduce la considerarea matricilor Jacobi, formate cu derivatele partiale in raport cu toate variabilele independente ale functiilor sistemului considerat.
Fie functia vectoriala ![]() , definita prin componentele
, definita prin componentele ![]() . Consideram matricea
jacobiana asociata lui
. Consideram matricea
jacobiana asociata lui ![]() in
in ![]()
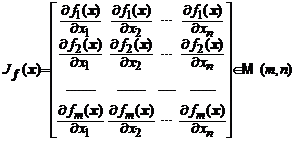 . (4)
. (4)
30.
Teorema. Fie ![]() o multime deschisa si
o multime deschisa si ![]() ,
, ![]() ,
, ![]() (
(![]() ) functii de clasa
) functii de clasa ![]() . Daca rangul matricii
jacobiene (4) asociate functiei
. Daca rangul matricii
jacobiene (4) asociate functiei ![]() ,
, ![]() in orice punct din
in orice punct din ![]() este egal cu
este egal cu ![]() (
(![]() ) atunci functiile
) atunci functiile ![]() sunt independente in multimea
deschisa
sunt independente in multimea
deschisa ![]() .
.
Demonstratie. Presupunem ca una din functii,
sa zicem, ![]() , se exprima in
, se exprima in ![]() , cu ajutorul celorlalte functii,
, cu ajutorul celorlalte functii, ![]() , printr-o relatie de forma (2'):
, printr-o relatie de forma (2'):
![]() oricare ar fi
oricare ar fi ![]() . (*)
. (*)
Atunci, prin derivarea in raport cu fiecare
din variabilele independente ![]() a acestei
identitati, obtinem sistemul de
a acestei
identitati, obtinem sistemul de ![]() identitati
(care pot fi eventual verificate si numai pe o parte a multimii
identitati
(care pot fi eventual verificate si numai pe o parte a multimii ![]() ):
):
![]() . (5)
. (5)
Fie ![]() a i. sistemul (5)
sa fie verificat in punctul
a i. sistemul (5)
sa fie verificat in punctul ![]() . Atunci sistemul (5) arata ca in punctul
. Atunci sistemul (5) arata ca in punctul ![]() , ultima linie a matricii jacobiene (4) este o
combinatie lineara a primelor
, ultima linie a matricii jacobiene (4) este o
combinatie lineara a primelor ![]() linii inmultite
respectiv cu factorii
linii inmultite
respectiv cu factorii ![]() si deci
si deci ![]() , ceea ce contrazice ipoteza teoremei.
, ceea ce contrazice ipoteza teoremei.
Asadar, identitatea (*) nu poate avea loc.
Vom prezenta fara demonstratie urmatoarea
31.
Teorema. Fie ![]() o multime deschisa si
o multime deschisa si ![]() ,
, ![]() ,
, ![]() (
(![]() ) functii de clasa
) functii de clasa ![]() . Daca, intr-un punct
. Daca, intr-un punct ![]() , rangul matricii
jacobiene (4) asociate functiei vectoriale
, rangul matricii
jacobiene (4) asociate functiei vectoriale ![]() ,
, ![]() este egal cu
este egal cu ![]() , adica,
, adica, ![]() , atunci exista o vecinatate
, atunci exista o vecinatate ![]() ,
, ![]() si
si ![]() functii, sa
zicem,
functii, sa
zicem, ![]() , care sunt independente
in vecinatatea
, care sunt independente
in vecinatatea ![]() , iar celelalte functii
, iar celelalte functii ![]() (desigur, cand
(desigur, cand ![]() ) sunt functional dependente de
) sunt functional dependente de ![]() , adica, pentru orice
, adica, pentru orice ![]() au loc relatiile:
au loc relatiile:
![]()
![]()
![]()
Exemplul 2. Analizam sistemul de functii definit in exemplul 1. Fie
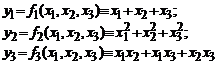 ,
,
unde ![]() .
.
Atunci ![]() si matricea lui
Jacobi are forma
si matricea lui
Jacobi are forma
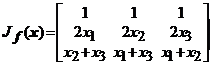 .
.
Daca adunam la linia
a treia elementele liniei a doua inmultite cu ![]() , obtinem o linie proportionala cu prima.
Asadar,
, obtinem o linie proportionala cu prima.
Asadar, ![]() si deci
functiile
si deci
functiile ![]() sunt functional
dependente in
sunt functional
dependente in ![]() . Se poate arata ca
. Se poate arata ca ![]() si atunci
doua functii sunt independente, iar a treia este functional
dependenta de aceste doua functii.
si atunci
doua functii sunt independente, iar a treia este functional
dependenta de aceste doua functii.
Exemplul 3. Fie sistemul de functii
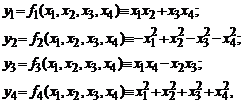
unde ![]() . Stabiliti dependenta sau independenta
sistemului de functii in punctul
. Stabiliti dependenta sau independenta
sistemului de functii in punctul ![]() .
.
Indicatie. Fie ![]() . Calculam matricea jacobiana
. Calculam matricea jacobiana ![]() :
:
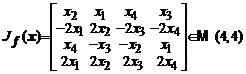 .
.
Atunci, in punctul ![]() avem
avem
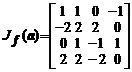 si
si ![]() ; deoarece
; deoarece 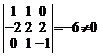 atunci
atunci ![]() si, in
consecinta, exista o vecinatate
si, in
consecinta, exista o vecinatate ![]() a punctului
a punctului ![]() a.i. functiile
a.i. functiile ![]() sa fie
independente in
sa fie
independente in ![]() .
.
Functia ![]() este dependenta
functional de functiile
este dependenta
functional de functiile ![]() si vom scrie
si vom scrie
![]() .
.
Extreme locale conditionate (extreme cu legaturi)
32. Fie ![]() o multime deschisa,
o multime deschisa, ![]() si functia
reala
si functia
reala ![]() ,
, ![]() .
.
Consideram sistemul ![]() de
de ![]() ,
, ![]() , functii reale definite pe multimea
, functii reale definite pe multimea ![]() ,
, ![]() ,
, ![]() si fie
si fie ![]() submultimea punctelor
din
submultimea punctelor
din ![]() care satisfac restrictiile sau legaturile sau ecuatiile
cuplate
care satisfac restrictiile sau legaturile sau ecuatiile
cuplate
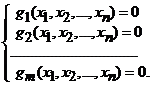 (1)
(1)
Asadar, ![]() reprezinta
multimea solutiilor sistemului (1), situate in
reprezinta
multimea solutiilor sistemului (1), situate in ![]() .
.
33.
Definitie. Punctul ![]() este maxim local conditionat (respectiv
un minim local conditionat) al functiei
este maxim local conditionat (respectiv
un minim local conditionat) al functiei ![]() restrictionata la multimea
restrictionata la multimea ![]() sau conditionat
de legaturile (1), daca exista o vecinatate
sau conditionat
de legaturile (1), daca exista o vecinatate ![]() , a.i. sa avem
, a.i. sa avem
![]() respectiv
respectiv ![]() . (2)
. (2)
A considera restrictia
functiei ![]() la multimea
la multimea ![]() inseamna a
considera valorile lui
inseamna a
considera valorile lui ![]() numai pentru acele
valori ale argumentelor
numai pentru acele
valori ale argumentelor ![]() care sunt solutii
ale sistemului (1). Altfel spus, cele
care sunt solutii
ale sistemului (1). Altfel spus, cele ![]() variabile independente
variabile independente
![]() sunt legate intre ele
prin cele
sunt legate intre ele
prin cele ![]() relatii (1).
relatii (1).
In continuare prezentam conditii
necesare pentru ca punctul ![]() sa fie extrem
conditionat al lui
sa fie extrem
conditionat al lui ![]() .
.
34.
Teorema. Presupunem
ca punctul ![]() este solutie a
sistemului (1) si intr-o vecinatate
este solutie a
sistemului (1) si intr-o vecinatate ![]() functiile
functiile ![]() si
si ![]() sunt de clasa
sunt de clasa ![]() (au derivate
partiale continue pe
(au derivate
partiale continue pe ![]() ). Mai mult, presupunem ca in punctul
). Mai mult, presupunem ca in punctul ![]() matricea
functionala
matricea
functionala
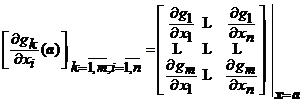 , (3)
, (3)
are rangul ![]() (
(![]() este numarul legaturilor independente din (1)),
este numarul legaturilor independente din (1)), 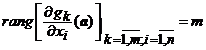 .
.
Daca ![]() este un punct de extrem local al lui
este un punct de extrem local al lui ![]() , conditionat de sistemul (1), atunci exista
, conditionat de sistemul (1), atunci exista ![]() numere
numere ![]() astfel incat sa
avem:
astfel incat sa
avem:
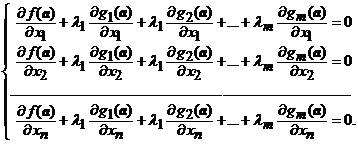 (4)
(4)
Demonstratie. Deoarece matricea functionala 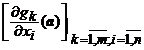 are, in punctul
are, in punctul ![]() , rangul
, rangul ![]() atunci exista un
determinant de ordin
atunci exista un
determinant de ordin ![]() al acestei matrice
care este nenul in punctul
al acestei matrice
care este nenul in punctul ![]() . Fara a restrange generalitatea, putem presupune
ca
. Fara a restrange generalitatea, putem presupune
ca
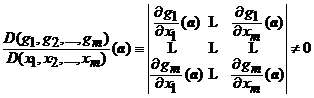 .
. ![]()
Atunci sistemul (1) poate fi rezolvat in
raport cu variabilele ![]() intr-o vecinatate
a punctului
intr-o vecinatate
a punctului ![]() . Intr-adevar, prin ipoteza avem
. Intr-adevar, prin ipoteza avem
![]() , adica functia
, adica functia ![]() se anuleaza in
punctul
se anuleaza in
punctul ![]() si are derivate
partiale continue intr-o vecinatate a punctului
si are derivate
partiale continue intr-o vecinatate a punctului ![]() , iar jacobianul acestor functii in raport cu
variabilele
, iar jacobianul acestor functii in raport cu
variabilele ![]() este nenul in
este nenul in ![]() . Din teorema functiilor implicite, rezulta ca
exista o vecinatate
. Din teorema functiilor implicite, rezulta ca
exista o vecinatate ![]() a punctului
a punctului ![]() si o
vecinatate
si o
vecinatate ![]() a punctului
a punctului ![]() si functiile
unic determinate, de clasa
si functiile
unic determinate, de clasa ![]() pe
pe ![]() ,
, ![]() astfel incat
astfel incat
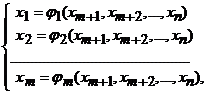 (5)
(5)
verifica conditiile ![]() si care sunt
solutii ale sistemului (1), adica
si care sunt
solutii ale sistemului (1), adica
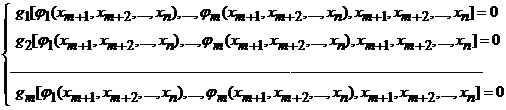 (6)
(6)
Este evident ca functiile ![]() , care apar in sistemul (6), depind numai de variabilele
independente
, care apar in sistemul (6), depind numai de variabilele
independente ![]() si
diferentialele acestor functii sunt nule pe
si
diferentialele acestor functii sunt nule pe ![]() , deci ele se anuleaza in punctul
, deci ele se anuleaza in punctul ![]() . Asadar, putem scrie relatiile:
. Asadar, putem scrie relatiile:
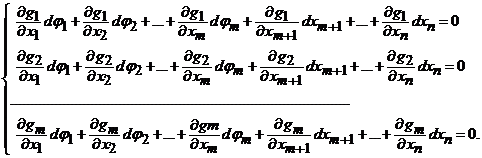 (7)
(7)
In relatiile (7), ![]() reprezinta
diferentialele functiilor
reprezinta
diferentialele functiilor ![]() calculate in
calculate in ![]() ,
, ![]() sunt variabile
independente, iar derivatele partiale ale functiilor
sunt variabile
independente, iar derivatele partiale ale functiilor ![]() sunt calculate in
punctul
sunt calculate in
punctul ![]() .
.
Substituim functiile ![]() in locul variabilele
corespunzatoare
in locul variabilele
corespunzatoare ![]() in
in ![]() . Expresia
obtinuta este o functie compusa (pe care o notam tot
cu
. Expresia
obtinuta este o functie compusa (pe care o notam tot
cu ![]() ) care depinde numai de variabilele independente
) care depinde numai de variabilele independente ![]() :
:
![]() (8)
(8)
Aratam ca daca functia
![]() are un maxim (minim)
local conditionat de sistemul (1) in punctul
are un maxim (minim)
local conditionat de sistemul (1) in punctul ![]() , atunci
, atunci ![]() are in punctul
are in punctul ![]() un maxim (minim)
obisnuit.
un maxim (minim)
obisnuit.
Intr-adevar, avem ![]() si presupunand de
exemplu, ca
si presupunand de
exemplu, ca ![]() este punct de maxim
conditionat pentru
este punct de maxim
conditionat pentru ![]() , atunci
, atunci
![]() ,
,
in orice punct ![]() care verifica
sistemul (1) si este situat intr-o anumita vecinatate a lui
care verifica
sistemul (1) si este situat intr-o anumita vecinatate a lui ![]() . Pentru
. Pentru ![]() , luand valorile
, luand valorile ![]() date de (5)
rezulta, potrivit relatiilor (6), ca punctul
date de (5)
rezulta, potrivit relatiilor (6), ca punctul ![]() verifica sistemul
(1), iar inegalitatea de mai sus se scrie, pe baza notatiei (8), sub forma
verifica sistemul
(1), iar inegalitatea de mai sus se scrie, pe baza notatiei (8), sub forma
![]()
deci, ![]() este maxim local pentru
este maxim local pentru ![]() si atunci este
necesar ca in punctul
si atunci este
necesar ca in punctul ![]() sa avem
sa avem
![]() (9)
(9)
De aici deducem ca
![]()
si deci, punctul ![]() este punct stationar pentru
este punct stationar pentru ![]() .
.
In consecinta, punctul ![]() este punct stationar pentru
este punct stationar pentru ![]() conditionat de sistemul (1) si atunci avem
conditionat de sistemul (1) si atunci avem
![]() (10)
(10)
Desigur, aici ![]() reprezinta
diferentialele functiilor
reprezinta
diferentialele functiilor ![]() calculate in punctul
calculate in punctul ![]() , iar
, iar ![]() sunt variabile
independente.
sunt variabile
independente.
Derivatele partiale ale functiei ![]() sunt calculate in
punctul
sunt calculate in
punctul ![]() .
.
Fie numerele reale ![]() , deocamdata oarecare. Inmultind respectiv
ecuatiile sistemului (7) cu aceste numere si apoi le adunam cu
(10) rezulta
, deocamdata oarecare. Inmultind respectiv
ecuatiile sistemului (7) cu aceste numere si apoi le adunam cu
(10) rezulta
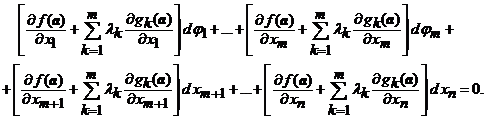 (11)
(11)
Determinam numerele ![]() a.i. incat
coeficientii diferentialelor
a.i. incat
coeficientii diferentialelor ![]() sa se anuleze.
sa se anuleze.
Asadar, avem
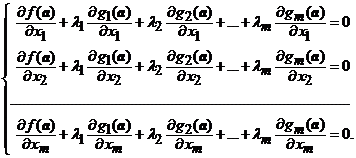 (4')
(4')
si cum determinantul coeficientilor lui ![]() este nenul in punctul
este nenul in punctul ![]() (vezi
(vezi ![]() ), rezulta ca aceste numere sunt bine determinate.
Cu valorile gasite pentru
), rezulta ca aceste numere sunt bine determinate.
Cu valorile gasite pentru ![]() relatia (11)
devine
relatia (11)
devine
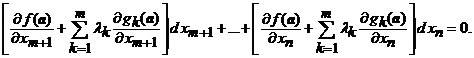 (12)
(12)
Aceasta relatie are loc pentru
orice valori ale variabilelor independente ![]() daca si
numai daca coeficientii acestor variabile se anuleaza:
daca si
numai daca coeficientii acestor variabile se anuleaza:
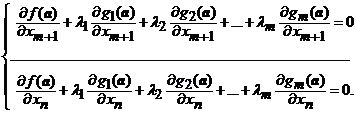 (4')
(4')
Sistemele (4') si (4') formeaza sistemul (4) si teorema este demonstrata.
35. Observatie. Orice
punct ![]() , solutie a sistemului (1) in care matricea
functionala
, solutie a sistemului (1) in care matricea
functionala 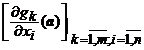 are rangul
are rangul ![]() si care
verifica sistemul (4) pentru anumite valori
si care
verifica sistemul (4) pentru anumite valori ![]() , se numeste punct
stationar al functiei
, se numeste punct
stationar al functiei ![]() conditionat de sistemul (1); coeficientii
conditionat de sistemul (1); coeficientii ![]() se numesc multiplicatorii lui Lagrange. este de la
sine inteles ca valorile parametrilor
se numesc multiplicatorii lui Lagrange. este de la
sine inteles ca valorile parametrilor ![]() se schimba
odata cu punctul stationar
se schimba
odata cu punctul stationar ![]() .
.
36. Observatie. Teorema afirma ca orice punct de extrem conditionat este un punct stationar conditionat. Reciproca nu este, in general, adevarata: adica exista puncte stationare conditionate in care functia nu are extreme conditionate.
37. Observatie.
Determinarea punctelor stationare conditionate, prin aceasta
metoda, se reduce la aflarea solutiilor a ![]() ecuatii (9) cu
necunoscutele
ecuatii (9) cu
necunoscutele ![]() dupa ce s-a
rezolvat sistemul (1) in necunoscutele
dupa ce s-a
rezolvat sistemul (1) in necunoscutele ![]() . In cele mai multe cazuri aceasta metoda este
practic imposibil de aplicat la rezolvarea anumitor probleme.
. In cele mai multe cazuri aceasta metoda este
practic imposibil de aplicat la rezolvarea anumitor probleme.
38. O metoda mai simpla pentru determinarea punctelor stationare conditionate este asa numita metoda multiplicatorilor lui Lagrange.
Vom observa ca in sistemul (4) apar tocmai derivatele partiale ale functiei
![]() ,
,
definita pentru orice ![]() .
.
Asadar, metoda multiplicatorilor lui Lagrange are la baza functia ajutatoare (numita lagrangian)
![]() , (13)
, (13)
definita pentru orice punct ![]() , unde
, unde ![]() sunt constante reale (numite
multiplicatorii lui Lagrange), deocamdata
necunoscute, care urmeaza a fi
determinate odata cu coordonatele punctelor stationare
sunt constante reale (numite
multiplicatorii lui Lagrange), deocamdata
necunoscute, care urmeaza a fi
determinate odata cu coordonatele punctelor stationare ![]() .
.
In acest scop vom privi functia
auxiliara (functia lui Lagrange) ![]() definita in (13)
ca functie care depinde de
definita in (13)
ca functie care depinde de ![]() variabilele; cele
variabilele; cele ![]() variabile independente
variabile independente
![]() si
si ![]() parametrii
parametrii ![]() .
.
Presupunem ca functia ![]() de clasa
de clasa ![]() . Punctul
. Punctul ![]() din
din ![]() este un punct stationar pentru
este un punct stationar pentru ![]() conditionat de
legaturile definite de sistemul (1), unde
conditionat de
legaturile definite de sistemul (1), unde ![]() ,
, ![]() sunt functii de
clasa
sunt functii de
clasa ![]() si
si ![]() daca si
numai daca punctul
daca si
numai daca punctul ![]() este punct stationar liber pentru
functia
este punct stationar liber pentru
functia
![]() .
.
Insa, pentru functia ![]() problema
determinarii punctelor de extrem
liber este cunoscuta.
problema
determinarii punctelor de extrem
liber este cunoscuta.
Asadar, pentru determinarea punctelor
stationare ale lui ![]() conditionate de
sistemul (1) procedam astfel:
conditionate de
sistemul (1) procedam astfel:
Pasul 1. Se defineste functia
ajutatoare (lagrangianul) 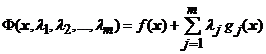 , pentru
, pentru ![]() si parametrii
reali nedeterminati
si parametrii
reali nedeterminati ![]() .
.
Pasul
2. Se anuleaza
derivatele partiale ale functiei ![]() :
:
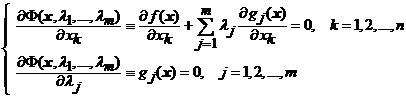 (14)
(14)
apoi se rezolva sistemul de ![]() ecuatii cu
ecuatii cu ![]() necunoscute,
necunoscute, ![]() .
.
Pasul 3. Daca ![]() este o solutie a
acestui sistem, atunci punctul
este o solutie a
acestui sistem, atunci punctul ![]() este punct stationar al lui
este punct stationar al lui ![]() , conditionat
de sistemul (1). Printre punctele stationare conditionate astfel
obtinute se afla si punctele de extrem conditionat ale lui
, conditionat
de sistemul (1). Printre punctele stationare conditionate astfel
obtinute se afla si punctele de extrem conditionat ale lui ![]() .
.
In continuare, prezentam conditii suficiente care sa permita sa identificam, dintre punctele stationare, unele puncte care pot fi de extrem conditionat.
Fie ![]() un punct stationar al lui
un punct stationar al lui ![]() conditionat de
sistemul (1). Deci,
conditionat de
sistemul (1). Deci, ![]() ,
, ![]() si exista
numerele reale
si exista
numerele reale ![]() astfel incat sa
fie verificat sistemul (4), adica punctul
astfel incat sa
fie verificat sistemul (4), adica punctul ![]() este solutie a
sistemului (14).
este solutie a
sistemului (14).
Vom cauta conditii suficiente de extrem conditionat.
Presupune ca functiile ![]() si
si ![]() ,
, ![]() sunt functii de
clasa
sunt functii de
clasa ![]() intr-o vecinatate
intr-o vecinatate
![]() a punctului
a punctului ![]() .
.
Pentru a vedea daca punctul ![]() este extrem
conditionat pentru
este extrem
conditionat pentru ![]() , trebuie sa studiem semnul diferentei
, trebuie sa studiem semnul diferentei
![]() ,
,
pentru![]() . Vom observa ca pentru astfel de puncte
. Vom observa ca pentru astfel de puncte ![]() , avem
, avem ![]() si in
consecinta
si in
consecinta ![]() .
.
Asadar, pentru punctele ![]() care verifica
sistemul (1), studiul semnului diferentei
care verifica
sistemul (1), studiul semnului diferentei ![]() se reduce la studiul
semnului diferentei
se reduce la studiul
semnului diferentei ![]() . Pe de alta parte, punctul
. Pe de alta parte, punctul ![]() verifica sistemul
(4), deci, este punct stationar obisnuit pentru functia
verifica sistemul
(4), deci, este punct stationar obisnuit pentru functia ![]() si atunci derivatele
sale partiale se anuleaza in
si atunci derivatele
sale partiale se anuleaza in ![]() .
.
Deoarece functia ![]() admite derivate
partiale de ordinul al doilea continue in vecinatatea
admite derivate
partiale de ordinul al doilea continue in vecinatatea ![]() atunci, pe baza
formulei lui Taylor de ordinul doi, putem scrie
atunci, pe baza
formulei lui Taylor de ordinul doi, putem scrie
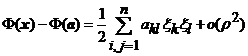 , (15)
, (15)
unde ![]() ;
; 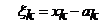 ,
, ![]() ,
,
![]() cand
cand 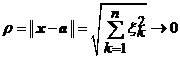 .
.
Relatia (15) pune in evidenta forma patratica 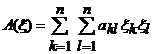 , a carei matrice asociata
, a carei matrice asociata ![]() este numita hessiana functiei
este numita hessiana functiei ![]() in punctul
in punctul ![]() .
.
Atunci, dupa cum se stie, semnul diferentei ![]() se studiaza
dupa modul cum este definita sau nu aceasta forma
patratica.
se studiaza
dupa modul cum este definita sau nu aceasta forma
patratica.
Exemplu. Sa se
determine extremele locale ale functiei ![]() ,
, ![]() cu legatura
cu legatura ![]() .
.
Solutie. Se scrie relatia de legatura
sub forma ![]() . Punctele din spatiul tridimnsional
. Punctele din spatiul tridimnsional ![]() care verifica
ecuatia de legatura sunt evident situate in planul
care verifica
ecuatia de legatura sunt evident situate in planul
![]() .
.
Functiile ![]() si
si ![]() sunt de clasa
sunt de clasa ![]() pe
pe ![]() si matricea
functionala
si matricea
functionala
![]() ,
,
are rangul egal cu ![]() in orice punct din
in orice punct din ![]() . In consecinta, eventualele puncte de extrem local ale lui
. In consecinta, eventualele puncte de extrem local ale lui ![]() , conditionate
de legatura
, conditionate
de legatura ![]() , se afla printre punctele
stationare (critice) ale
functiei
, se afla printre punctele
stationare (critice) ale
functiei ![]() conditionate de ecuatia
conditionate de ecuatia ![]() , sau echivalent, aceste puncte de extrem conditionat se
afla printre punctele
stationare (critice)
obisnuite ale functiei ajutatoare (lagrangianul problemei)
, sau echivalent, aceste puncte de extrem conditionat se
afla printre punctele
stationare (critice)
obisnuite ale functiei ajutatoare (lagrangianul problemei)
![]() .
.
unde constanta ![]() , deocamdata necunoscuta, este multiplicatorul lui Lagrange.
, deocamdata necunoscuta, este multiplicatorul lui Lagrange.
Determinam punctele stationare ale
functiei ![]() . Avem
. Avem
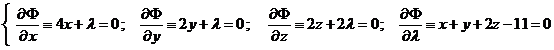 .
.
Rezolvand acest sistem obtinem punctul stationar, ![]() corespunzator
multiplicatorului Lagrange
corespunzator
multiplicatorului Lagrange ![]() . Lagrangianul problemei are forma
. Lagrangianul problemei are forma
![]() .
.
In punctul stationar ![]() , forma patratica are expresia
, forma patratica are expresia
![]()
In consecinta,
punctul stationar este punct de minim
local conditionat. Valoarea minima in acest punct este egala
cu ![]() .
.
39. Analizam problema urmatoare:
Fie functia ![]() ,
, ![]() si
consideram un sistem de cel mult doua functii
si
consideram un sistem de cel mult doua functii ![]() (numarul de
functii
(numarul de
functii ![]() ,
, ![]() , trebuie sa fie strict mai mic decat numarul
variabilelor independente
, trebuie sa fie strict mai mic decat numarul
variabilelor independente ![]() ).
).
In continuare, alegem ![]() si definim
multimea
si definim
multimea
![]() ,
,
Evident, multimea ![]() este formata din
punctele
este formata din
punctele ![]() care verifica legatura
care verifica legatura ![]() (adica, din acele
puncte situate in
(adica, din acele
puncte situate in ![]() si care se
afla pe suprafata definita de ecuatia
si care se
afla pe suprafata definita de ecuatia ![]() ). Presupunem ca functiile
). Presupunem ca functiile ![]() si
si ![]() sunt de clasa
sunt de clasa ![]() si in plus
si in plus ![]() in
in ![]() .
.
40.
Propozitie. Punctul 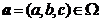 este un punct de
stationar pentru
este un punct de
stationar pentru ![]() supus la legatura
supus la legatura
![]() , adica
, adica ![]() daca si
numai daca punctul
daca si
numai daca punctul 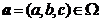 este punct
stationar obisnuit (liber) pentru functia lagrangiana
este punct
stationar obisnuit (liber) pentru functia lagrangiana
![]() . (16)
. (16)
Demonstratie. "![]() " Deoarece functiile
" Deoarece functiile ![]() atunci functia
atunci functia ![]() este de clasa
este de clasa ![]() . Presupunem ca punctul
. Presupunem ca punctul ![]() este un punct
stationar pentru functia
este un punct
stationar pentru functia ![]() . Atunci acest punct verifica sistemul:
. Atunci acest punct verifica sistemul:
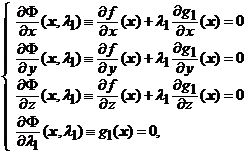 (17)
(17)
adica
exista ![]() si numarul
real
si numarul
real ![]() a.i. sa se verifice
sistemul:
a.i. sa se verifice
sistemul:
![]() .
.
Presupunem ca punctul ![]() este un punct de maxim
local (liber) pentru functia
este un punct de maxim
local (liber) pentru functia ![]() . Atunci exista o vecinatate
. Atunci exista o vecinatate ![]() ,
, ![]() a.i.
a.i.
![]() , pentru orice
, pentru orice ![]() .
.
Tinand seama de definitia lagrangianului aceasta inegalitate se scrie sub forma
![]() , oricare ar fi
, oricare ar fi ![]() .
.
Deoarece ![]() si punctele
si punctele ![]() apartin
vecinatatii
apartin
vecinatatii ![]() care este inclusa
in
care este inclusa
in ![]() , atunci evident, in aceste puncte avem si
, atunci evident, in aceste puncte avem si ![]() si ultima
inegalitate devine
si ultima
inegalitate devine
![]() ,
,
relatie care arata ca punctul  este punct de maxim
pentru
este punct de maxim
pentru ![]() care verifica
legatura
care verifica
legatura ![]() .
.
"![]() " Pentru a arata aceasta implicatie, fie
punctul
" Pentru a arata aceasta implicatie, fie
punctul ![]() un punct de maxim
pentru
un punct de maxim
pentru ![]() si care
verifica conditiile
si care
verifica conditiile ![]() si
si ![]() . Atunci, din teorema functiilor implicite, rezulta
ca exista o vecinatate
. Atunci, din teorema functiilor implicite, rezulta
ca exista o vecinatate ![]() si o
vecinatate
si o
vecinatate ![]() si o unica
functie
si o unica
functie ![]() , a.i.
, a.i. ![]() pe
pe ![]() si care
verifica conditia
si care
verifica conditia ![]() . In plus functia
. In plus functia ![]() este derivabila
pe
este derivabila
pe ![]() .
.
Derivand relatia ![]() putem scrie:
putem scrie:
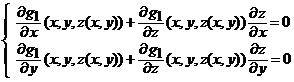 (18)
(18)
Substituind variabila ![]() in expresia lui
in expresia lui ![]() obtinem o
functie
obtinem o
functie ![]() de doua variabile
independente, definita prin
de doua variabile
independente, definita prin
![]() si
si ![]() . (19)
. (19)
Avem
![]() ,
,
pentru orice ![]() apartinand unei
anumite vecinatati
apartinand unei
anumite vecinatati ![]() a punctului
a punctului ![]() . Aceasta inegalitate arata ca daca
punctul
. Aceasta inegalitate arata ca daca
punctul ![]() este maxim
conditionat pentru
este maxim
conditionat pentru ![]() , atunci punctul
, atunci punctul ![]() este maxim liber
(obisnuit) pentru functia
este maxim liber
(obisnuit) pentru functia ![]() . Din teorema lui Fermat avem
. Din teorema lui Fermat avem
![]()
Asadar, avem
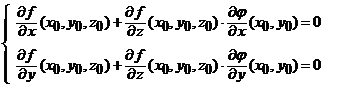 si
si ![]() (20)
(20)
Inmultind relatiile (18) cu
constanta ![]() si apoi
adunam cu (20) avem
si apoi
adunam cu (20) avem
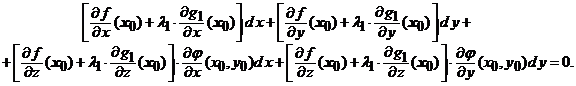
Vom scrie aceasta relatie sub forma echivalenta
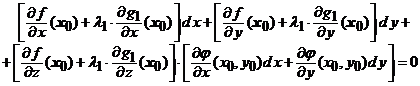
sau
![]() , (21)
, (21)
unde am folosit ![]() (aici s-a folosit
invarianta diferentialei de ordinul intai) . Cum relatia (21)
este posibila daca si numai daca coeficientii
marimilor independente
(aici s-a folosit
invarianta diferentialei de ordinul intai) . Cum relatia (21)
este posibila daca si numai daca coeficientii
marimilor independente ![]() sunt nuli, atunci din
aceasta relatie putem determina valoarea constantei
sunt nuli, atunci din
aceasta relatie putem determina valoarea constantei ![]() . Avem
. Avem
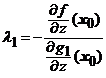 .
.
Observam ca relatia (21) poate fi scrisa sub forma
![]() , (22)
, (22)
care arata ca punctul ![]() este punct
stationar obisnuit pentru functia lui Lagrange
este punct
stationar obisnuit pentru functia lui Lagrange
![]() . (23)
. (23)
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |