
Functii reale de mai multe variabile reale. Limite, continuitate, uniform continuitate
1. Definitie.
Fie ![]() o multime si
o multime si
![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() si
si ![]() o functie
reala de
o functie
reala de ![]() - variabile reale,
- variabile reale, ![]() . Numarul real
. Numarul real ![]() este limita functiei
este limita functiei ![]() in punctul
in punctul ![]() si scriem
si scriem ![]() , daca pentru orice vecinatate
, daca pentru orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() a.i.
a.i. ![]() .
.
2. Observatie.
(1). Fie ![]() si
si ![]() . Atunci
. Atunci ![]() si uneori scriem
si uneori scriem ![]() .
.
Se observa ca in punctul ![]() functia
functia ![]() nu este neaparat
definita si daca este definita atunci in definitia
limitei se ia
nu este neaparat
definita si daca este definita atunci in definitia
limitei se ia ![]() .
.
Daca se tine seama de
definitia vecinatatii unui punct, atunci ![]() este limita
functiei
este limita
functiei ![]() in punctul
in punctul ![]() daca si
numai daca pentru orice vecinatate
daca si
numai daca pentru orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() si
si ![]() sa avem
sa avem ![]() .
.
Numarul ![]() este limita
functiei
este limita
functiei ![]() in punctul
in punctul ![]() daca si
numai daca oricare ar fi sirul de puncte
daca si
numai daca oricare ar fi sirul de puncte ![]() din
din ![]() , cu
, cu ![]() si
si ![]() sa avem
sa avem ![]() .
.
Limita ![]() exista si
este finita daca si numai daca
exista si
este finita daca si numai daca ![]() astfel incat oricare
ar fi
astfel incat oricare
ar fi ![]() ,
, ![]() si
si ![]() sa avem
sa avem ![]() .
.
Limita functiei ![]() in punctul
in punctul ![]() este egala cu
este egala cu ![]() (respectiv cu
(respectiv cu ![]() ) si scriem
) si scriem ![]() , daca si numai daca
, daca si numai daca ![]() astfel ca,
oricare ar fi
astfel ca,
oricare ar fi ![]() , cu
, cu ![]() sa avem
sa avem ![]() (respectiv
(respectiv ![]() ) sau echivalent pentru orice interval
) sau echivalent pentru orice interval ![]() exista sfera
exista sfera ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() ,
, ![]() , sa avem
, sa avem ![]() .
.
3.
Propozitie. Fie ![]() o multime,
si
o multime,
si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() si
si ![]() . Presupunem ca
functiile
. Presupunem ca
functiile ![]() si
si ![]() au limite finite in
punctul
au limite finite in
punctul ![]() . Atunci
. Atunci
functiile ![]() au limita in
punctul
au limita in
punctul ![]() si avem
si avem
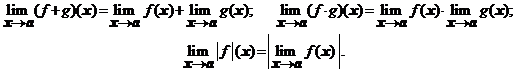
daca ![]() pentru orice
pentru orice ![]() si
si ![]() , atunci functia
, atunci functia ![]() are limita in
are limita in ![]() si avem
si avem
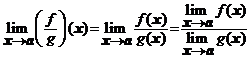 .
.
4.
Definitie. Fie ![]() o multime,
o multime, ![]() si
si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() , atunci functia
, atunci functia ![]() este continua in
este continua in ![]() daca si
numai daca
daca si
numai daca ![]() are limita
are limita ![]() in punctul
in punctul ![]() .
.
Altfel spus, functia ![]() este continua in
punctul
este continua in
punctul ![]() daca si
numai daca
daca si
numai daca ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() cu
cu ![]() sa avem
sa avem ![]() .
.
5. Definitie.
Fie ![]() o multime,
o multime, ![]() . Functia
. Functia ![]() este uniform continua pe
este uniform continua pe ![]() daca si
numai daca
daca si
numai daca ![]() a.i. pentru orice
a.i. pentru orice ![]() cu
cu ![]()
![]()
![]() .
.
Limite iterate
6.
Definitie. Fie ![]() o multime
deschisa si functia
o multime
deschisa si functia ![]() ,
, ![]() si fie punctul
si fie punctul ![]() . Daca
. Daca ![]() este punct de
acumulare al multimii
este punct de
acumulare al multimii
![]() ,
,
atunci putem
considera limita functiei ![]() ,
,
![]() ,
,
ca in cazul unei
singure variabile. Aceasta limita este un numar ce depinde de
celelalte ![]() - variabile reale, diferite de
- variabile reale, diferite de ![]() .
.
Se poate considera limita
![]() ,
,
care este un numar ce depinde de celelalte ![]() - variabile reale, diferite de
- variabile reale, diferite de ![]() si
si ![]() . Analog, putem considera limita functiei
. Analog, putem considera limita functiei ![]() in raport cu toate
variabilele luate pe rand. Aceasta limita este un numar care nu
mai depinde de nici una din variabilele
in raport cu toate
variabilele luate pe rand. Aceasta limita este un numar care nu
mai depinde de nici una din variabilele ![]() . Aceasta limita se numeste limita iterata a functiei
. Aceasta limita se numeste limita iterata a functiei ![]() .
.
De exemplu, pentru functiile de
doua variabile, ![]() ,
, ![]() putem scrie limitele
iterate
putem scrie limitele
iterate
![]() si
si ![]() . (1)
. (1)
Asadar, pentru o functiie de
doua variabile, ![]() ,
, ![]() putem considera limitele:
putem considera limitele:
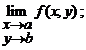
![]() si
si ![]() . (2)
. (2)
Urmatoarea propozitie arata legatura intre limita si limitele iterate:
Propozitie. Fie ![]() ,
, ![]() . Daca exista limita functiei intr-un punct
si limitele iterate in acel punct, atunci ele sunt egale.
. Daca exista limita functiei intr-un punct
si limitele iterate in acel punct, atunci ele sunt egale.
Demonstratie. Fara a restrange generalitatea,
vom considera cazul functiilor de doua variabile, ![]() ,
, ![]() . Fie
. Fie ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() . Presupunem ca exista limita
. Presupunem ca exista limita 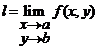 si limita
iterata
si limita
iterata ![]() si dunt finite.
Aratam ca
si dunt finite.
Aratam ca ![]() .
.
Notam cu ![]() , proiectia multimii
, proiectia multimii ![]() pe axa
pe axa ![]() si presupunem ca
si presupunem ca ![]() este punct de
acumulare pentru
este punct de
acumulare pentru ![]() . Fie
. Fie ![]() oarecare. Atunci,
pentru orice
oarecare. Atunci,
pentru orice ![]() , exista limita simpla in raport cu
, exista limita simpla in raport cu ![]() ,
, ![]() . Prin ipoteza, functia
. Prin ipoteza, functia ![]() are limita in
are limita in ![]() si putem scrie
si putem scrie ![]() . Fie
. Fie ![]() oarecare, dar fixat.
Deoarece
oarecare, dar fixat.
Deoarece 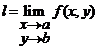 , atunci exista o vecinatate
, atunci exista o vecinatate ![]() a.i. sa avem
a.i. sa avem ![]() , oricare ar fi
, oricare ar fi ![]() , cu
, cu ![]() . Cum pentru fiecare
. Cum pentru fiecare ![]() , fixat, exista
, fixat, exista ![]() , atunci pentru
, atunci pentru ![]() a.i.
a.i. ![]() , prin trecerea la limita in inegalitatea
, prin trecerea la limita in inegalitatea ![]() , avem
, avem ![]() , pentru orice
, pentru orice ![]() cu
cu ![]() .
.
Asadar, putem scrie ![]() , si cum
, si cum ![]() este oarecare,
este oarecare, ![]() .
.
8. Observatie. (1). Daca exista numai una din cele trei limite
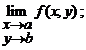
![]() sau
sau ![]() ,
,
nu rezulta ca si celelalte doua limite exista (este posibil ca numai una sau doua din aceste limite sa existe).
De exemplu, functia ![]() definita prin
definita prin 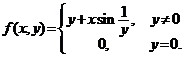 , are limita in punctul
, are limita in punctul ![]() ;
; 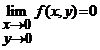 . Exista limita iterata
. Exista limita iterata ![]() si este
egala cu zero insa limita iterata
si este
egala cu zero insa limita iterata ![]() nu exista.
nu exista.
Solutie. Pentru ![]() , putem scrie
, putem scrie
![]() , cand
, cand ![]() ;
;
si avem 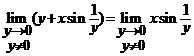 , care evident nu exista si
, care evident nu exista si 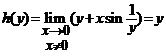 ;
;
Asadar, 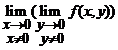 nu exista,
insa
nu exista,
insa 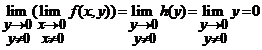 .
.
(2). Functiile ![]() definite prin
definite prin
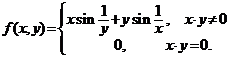 si respectiv
si respectiv 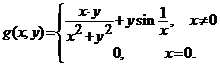 ,
,
au in origine numai una din cele trei limite.
(3). Daca nu exista limita 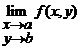 atunci limitele
iterate pot exista si sa fie diferite.
atunci limitele
iterate pot exista si sa fie diferite.
De exemplu, pentru functia ![]() definita prin
definita prin 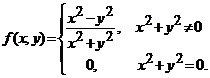 , exista limitele iterate in origine si acestea
sunt diferite;
, exista limitele iterate in origine si acestea
sunt diferite; ![]() si
si ![]() .
.
(4). Este posibil ca punctul ![]() sa fie punct de
acumulare pentru
sa fie punct de
acumulare pentru ![]() insa,
multimea
insa,
multimea ![]() proiectia a
multimii
proiectia a
multimii ![]() pe axa
pe axa ![]() , sa nu aiba pe
, sa nu aiba pe ![]() ca punct de acumulare
oricare ar fi
ca punct de acumulare
oricare ar fi ![]() si, atunci nu are sens
si, atunci nu are sens ![]() . De exemplu, daca
. De exemplu, daca ![]() este formata
dintr-un segment de dreapta paralel cu axa
este formata
dintr-un segment de dreapta paralel cu axa ![]() , atunci proiectia
, atunci proiectia ![]() pe axa
pe axa ![]() se reduce la un punct.
se reduce la un punct.
(5). Exista functii
pentru care limita ![]() exista
uniforma in raport cu
exista
uniforma in raport cu ![]() , limita
, limita ![]() exista
uniforma in raport cu
exista
uniforma in raport cu ![]() si avem
si avem ![]() dar nu exista
dar nu exista 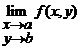 ; de exemplu, pentru functia
; de exemplu, pentru functia ![]() definita prin
definita prin ![]() , exista
, exista ![]() uniforma in
raport cu
uniforma in
raport cu ![]() si
si ![]() .
.
Limite si continuitatea functiilor vectoriale de variabile vectoriale
Fie ![]() si
si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() si fie
functiile reale
si fie
functiile reale ![]() ,
, ![]() . Atunci functia vectoriala
. Atunci functia vectoriala ![]() este definita
si complet determinata prin componentele sale reale
este definita
si complet determinata prin componentele sale reale ![]() .
.
.9.
Definitie. Functia
![]() are limita in punctul
are limita in punctul ![]() , daca exista
, daca exista ![]() cu proprietatea
ca
cu proprietatea
ca
pentru ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() cu
cu ![]() sa avem
sa avem ![]() .
.
Este evident ca daca limita ![]() exista atunci ea
este unica.
exista atunci ea
este unica.
In cazul functiilor reale de variabile
vectoriale, ![]() , limita
, limita ![]() poate fi
poate fi ![]() si
si ![]() .
.
10. Definitie.
Functia vectoriala ![]() este continua in punctul de acumulare
este continua in punctul de acumulare ![]() daca si
numai daca functia
daca si
numai daca functia ![]() are in punctul
are in punctul ![]() limita egala
cu
limita egala
cu ![]() .
.
Altfel spus, functia ![]() este continua in
punctul
este continua in
punctul ![]() daca si
numai daca
daca si
numai daca ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() cu
cu ![]() sa avem
sa avem ![]() .
.
Daca functia ![]() este continua in
orice punct
este continua in
orice punct ![]() atunci spunem ca
functia
atunci spunem ca
functia ![]() este continua pe
este continua pe ![]()
11. Propozitie.
Functia vectoriala ![]() este continua
intr-un punct
este continua
intr-un punct ![]() daca si
numai daca fiecare din componentele sale reale
daca si
numai daca fiecare din componentele sale reale ![]() este functie
continua in
este functie
continua in ![]() .
.
Demonstratie. Deoarece au loc inegalitatile
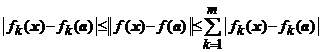 ,
, ![]() ,
,
atunci aplicand, de
exemplu, definitia cu ![]() si
si ![]() rezulta ca
afirmatia propozitiei este adevarata.
rezulta ca
afirmatia propozitiei este adevarata.
12.
Definitie. Functia
vectoriala ![]() este uniform continua pe
este uniform continua pe ![]() daca si
numai daca
daca si
numai daca ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() cu
cu ![]() sa avem
sa avem ![]() .
.
13. Propozitie.
Functia vectoriala ![]() este uniform continua pe
este uniform continua pe ![]() daca si
numai daca fiecare din componentele sale reale
daca si
numai daca fiecare din componentele sale reale ![]() este uniform
contiua continua pe
este uniform
contiua continua pe ![]() .
.
14.
Propozitie. Daca
functia vectoriala ![]() este uniform continua pe
este uniform continua pe ![]() atunci
atunci ![]() este contiua
continua pe
este contiua
continua pe ![]() .
.
15. Propozitie.
Fie ![]() o multime
compacta. Daca functia vectoriala
o multime
compacta. Daca functia vectoriala ![]() este continua pe
este continua pe ![]() atunci
atunci ![]() este uniform
contiua continua pe
este uniform
contiua continua pe ![]() .
.
Demonstratie. Prin ipoteza, multimea ![]() este compacta,
deci este inchisa si marginita. Presupunem ca
este compacta,
deci este inchisa si marginita. Presupunem ca ![]() nu este uniform
continua pe
nu este uniform
continua pe ![]() . Atunci, negand definitia uniform
continuitatii, putem scrie:
. Atunci, negand definitia uniform
continuitatii, putem scrie:
![]() a. i. pentru orice
a. i. pentru orice ![]() (suficient de mic) in
particular, putem alege
(suficient de mic) in
particular, putem alege ![]() ,
, ![]() , exista sirurile
, exista sirurile 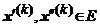 cu proprietatea
cu proprietatea ![]() sa avem
sa avem ![]() .
.
Deoarece, multimea ![]() este
marginita atunci sirul
este
marginita atunci sirul ![]() este marginit,
deci contine un subsir convergent. Fie acesta
este marginit,
deci contine un subsir convergent. Fie acesta ![]() si
si ![]() . Cum
. Cum ![]() este inchisa
si
este inchisa
si ![]() este punct limita
pentru multimea termenilor subsirului considerat, deci pentru
este punct limita
pentru multimea termenilor subsirului considerat, deci pentru ![]() , rezulta ca
, rezulta ca ![]() . Analog gasim
. Analog gasim ![]() . Din inegalitatile
. Din inegalitatile ![]() , trecand la limita rexulta ca
, trecand la limita rexulta ca ![]() . Folosind
continuitatea lui
. Folosind
continuitatea lui ![]() deducem ca
deducem ca ![]() si
si ![]() .
.
Din evaluarile
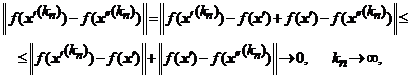
deducem ca diferenta ![]() , incepand de la un
anumit rang, ramane mai mica decat
, incepand de la un
anumit rang, ramane mai mica decat ![]() , ceea ce contrazice presupunerea facuta.
, ceea ce contrazice presupunerea facuta.
Continuitatea partiala a functiilor vectoriale de variabile vectoriale
16.
Definitie. Functia
vectoriala ![]() ,
, ![]() este continua partial in raport cu
punctul
este continua partial in raport cu
punctul ![]() in punctul de
acumulare
in punctul de
acumulare ![]() daca si
numai daca pentru orice
daca si
numai daca pentru orice ![]() , exista
, exista ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() cu
cu ![]() si
si ![]() sa avem
sa avem
![]() ,
,
Propozitie. Daca functia
![]() este continua
intr-un punct
este continua
intr-un punct ![]() (deci este
continua in ansamblul variabilelor), atunci ea este continua in acest
punct in raport cu fiecare variabila.
(deci este
continua in ansamblul variabilelor), atunci ea este continua in acest
punct in raport cu fiecare variabila.
Exemple. (1).
Fie ![]() si functia
si functia ![]() , definita prin
, definita prin ![]() . Aratati ca
. Aratati ca 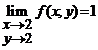 .
.
Solutie. Fie ![]() , oarecare, fixat. Daca alegem
, oarecare, fixat. Daca alegem ![]() , atunci pentru
, atunci pentru ![]() si
si ![]() , putem avea (de exemplu, pentru orice
, putem avea (de exemplu, pentru orice ![]() )
) 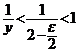 si atunci deducem
si atunci deducem
![]() .
.
Aratati ca 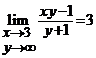 .
.
Solutie. Fie ![]() oarecare. Deoarece
oarecare. Deoarece ![]() , putem alege
, putem alege ![]() si pentru
si pentru ![]() avem
avem
![]()
in orice vecinatate a punctului ![]() , de forma
, de forma ![]() .
.
Aratati ca functia ![]() , nu are limita in punctul
, nu are limita in punctul ![]() .
.
Solutie. Consideram sirul de puncte ![]() , cand
, cand ![]() . Atunci sirul valorilor
. Atunci sirul valorilor ![]() ,
, ![]() . Alegand un alt sir de puncte, de exemplu, sirul
. Alegand un alt sir de puncte, de exemplu, sirul ![]() , cand
, cand ![]() atunci sirul
valorilor
atunci sirul
valorilor ![]() ,
, ![]() . Asadar, observam ca pentru doua
siruri diferite, care tind catre punctul
. Asadar, observam ca pentru doua
siruri diferite, care tind catre punctul ![]() , atunci se obtin limite diferite, ceea ce contrazice
unicitatea limitei functiei intr-un punct.
, atunci se obtin limite diferite, ceea ce contrazice
unicitatea limitei functiei intr-un punct.
Aratati ca functia 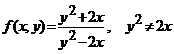 , nu are limita in punctul
, nu are limita in punctul ![]() .
.
Indicatie. Alegem, de exemplu, directiile ![]() , cu
, cu ![]() si
si ![]() . Atunci limita
. Atunci limita
![]() , evident, depinde de
, evident, depinde de
![]() .
.
(5). Fie functia ![]() ,
, 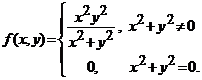 . Aratati
ca
. Aratati
ca ![]() este continua pe
este continua pe ![]() .
.
Solutie. In orice punct diferit ![]() functia
functia ![]() este continua
deoarece este definita printr-un raport de functii continue. Din
inegalitatile succesive,
este continua
deoarece este definita printr-un raport de functii continue. Din
inegalitatile succesive,
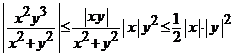 ,
,
rezulta ca 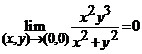 si deci
si deci ![]() este continua
si in punctul
este continua
si in punctul ![]() .
.
Fie ![]() un spatiu metric.
Functia distanta
un spatiu metric.
Functia distanta ![]() ,
, ![]() , este o functie
continua in ambele variabile
, este o functie
continua in ambele variabile ![]() .
.
Demonstratie.
Fie sirurile ![]() si
si ![]() . Atunci, putem scrie
. Atunci, putem scrie
![]()
si
![]() .
.
Asadar, avem ![]() , deci
, deci ![]() , ceea ce arata continuitatea functiei
distanta.
, ceea ce arata continuitatea functiei
distanta.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |