CODURI CONVOLUTIONALE
In general, un cod convolutional este complet determinat daca se cunosc polinoamele generatoare, care definesc:
numarul de celule ale registrului de deplasare (dat de gradul maxim al acestora-1);
numarul de sumatoare modulo 2 (dat de numarul de polinoame);
conexiunile intre celulele registrului si aceste sumatoare.
Exemplu
Sa se implementeze codorul definit de polinoamele
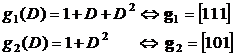
si sa se determine cuvantul de cod daca secventa de date este w=
Codorul are o intrare, 2 iesiri, registrul de deplasare este format din 2 celule, iar rata codului este R=1/2. Structura codorului este reprezentata in figura 6.2.
Bitii de intrare sunt introdusi in registrul de deplasare de la stanga la dreapta. Pentru fiecare bit de intrare introdus in codor sunt generati cate doi biti la iesirea celor doua sumatoare modulo 2. In acest fel fiecare bit de intrare influenteaza semnalul la iesire atat pe intervalul de tact in care acesta a fost introdus cat si pe urmatoarele doua intervale de tact. Cele doua sumatoare sunt citite alternativ, astfel incat rata codului este dubla fata de rata secventei de intrare.
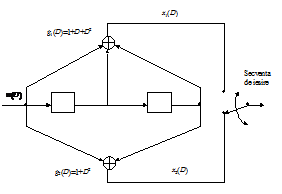
-Fig.6.2. Structura codorului convolutional cu rata 1/2 din exemplul 6.1.
Atat secventele de intrare cat si polinoamele generatoare se pot defini se pot defini polinomial sau vectorial. Secventa de intrare se poate scrie astfel
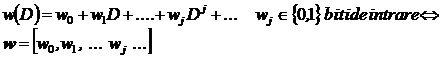 (30)
(30)
Pentru structura din exemplul 6.1. secventele la iesirea celor doua sumatoare sunt
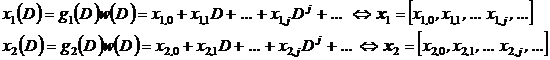 (31)
(31)
Cele doua iesiri sunt intretesute pentru a genera secventa la iesire:
![]() (32)
(32)
Cu acestea, pentru secventa de intrare particulara data,
![]() (33)
(33)
se pot determina secventele la iesirea celor doua sumatoare
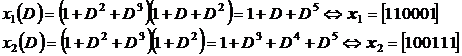 (34)
(34)
deci secventa de cod generata este
![]() (35)
(35)
diagrama de tranzitii este se poate determina din tabelul de tranzitii Tabelul 6.1.
Tabelul 6.1.
|
Starea curenta |
Intrare |
Starea urmatoare |
Iesire |
|
| |||
Aceasta este reprezentat schematic in figura 6.3.
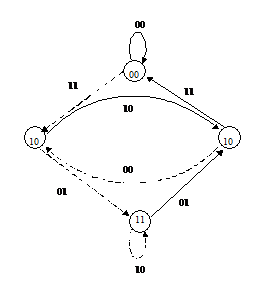
Fig.6.3. Diagrama de tranzitie a starilor pentru codorul convolutional din exemplul 6.1.
Descrierea codoarelor prin diagrama trellis
Codoarele folosite pentru coduri convolutionale mai pot fi descrise si cu ajutorul diagramelor trellis care permit o vizualizare a evolutiei atat in spatiul starilor cat si in timp. Astfel pe verticala se reprezinta toate starile posibile ale codorului, la fiecare moment de timp. Un bit de intrare "0" va determina trecerea codorului intr-o alta stare, trecere ce va fi reprezentata printr-o linie continua ce uneste starea de pornire de la momentul discret t si starea urmatoare de la momentul (t+1). Trecerile datorate bitilor de intrare "1" sunt reprezentate prin linii punctate. Deasupra acestora sunt trecuti bitii care apar la iesirea codorului. Pe masura ce codorul evolueaza in spatiul starilor se realizeaza o deplasare de la dreapta la stanga prin diagrama trellis, iar secventa de date codata se poate citi urmarind datele trecute deasupra liniilor parcurse. Pentru codorul descris in exemplul 6.1. diagrama trellis este reprezentata in figura 6.4.

Fig.6.4. Diagrama trellis asociata codorului din exemplul 6.1.
Decodarea codurilor convolutionale: algoritmul Viterbi
Algoritmul Viterbi poate fi exprimat sintetic prin urmatoarea procedura:
Pasul 1. Se incepe de la adancimea j=1. Se determina metrica pentru fiecare cale care intra intr-una din starile urmatoare, si se memoreaza starea in care a ajuns, metrica asociata si calea parcursa.
Pasul 2. Pentru fiecare j=j+1 se determina metricile partiale pentru toate caile emergente unei anumite stari astfel:
metrica supravietuitorului (adancimea j)+ metrica caii care intra in starea urmatoare
Pentru fiecare stare se pastreaza metrica maxima (supravietuitoare), cealalta fiind eliminata. Se memoreaza de fiecare data starea, metrica si calea supravietuitoare asociata
Pasul 3. Daca j L+m se repeta punctul 2. Altfel algoritmul se termina
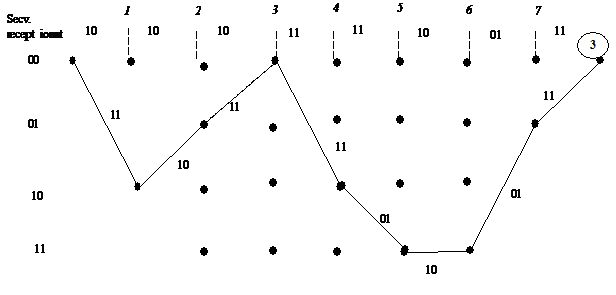
Diagrama trellis la momentul t=8T
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |