Spatii vectoriale
1.
Definitie. Fie ![]() un grup comutativ
si
un grup comutativ
si ![]() un corp comutativ cu
elementul unitate
un corp comutativ cu
elementul unitate![]() . Consideram o aplicatie externa definita
pe produsul cartezian
. Consideram o aplicatie externa definita
pe produsul cartezian ![]() , notata
, notata ![]() , unde
, unde ![]() si
si ![]() , cu proprietatile:
, cu proprietatile:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
![]() ,
,
oricare ar fi ![]() si
si ![]() .
.
Grupul comutativ ![]() inzestrat cu legea
externa care verifica axiomele (1)-(4) se numeste spatiu vectorial peste corpul comutativ
inzestrat cu legea
externa care verifica axiomele (1)-(4) se numeste spatiu vectorial peste corpul comutativ
![]() . Vom numi punct
orice element al unui spatiu vectorial. Deoarece vectorii liberi din
. Vom numi punct
orice element al unui spatiu vectorial. Deoarece vectorii liberi din ![]() respectiv,
respectiv, ![]() , verifica toate axiomele de mai inainte, uneori este
avantajos sa interpretam elementele (punctele) spatiului
, verifica toate axiomele de mai inainte, uneori este
avantajos sa interpretam elementele (punctele) spatiului ![]() ca vectori. De obicei,
ca vectori. De obicei, ![]() este corpul
este corpul ![]() al numerelor reale sau
corpul
al numerelor reale sau
corpul ![]() al numerelor complexe.
In primul caz,
al numerelor complexe.
In primul caz, ![]() se numeste spatiu vectorial real, iar in al
doilea caz
se numeste spatiu vectorial real, iar in al
doilea caz ![]() este numit spatiu vectorial complex.
este numit spatiu vectorial complex.
In continuare vom considera numai spatiile vectoriale reale.
2. Un spatiu vectorial ![]() se numeste normat daca exista
aplicatia
se numeste normat daca exista
aplicatia ![]() , numita norma
pe
, numita norma
pe ![]() , care verifica axiomele:
, care verifica axiomele:
1) ![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() daca si
numai daca
daca si
numai daca ![]() (unde
(unde ![]() este elementul neutru
este elementul neutru
al
grupului abelian ![]() ).
).
![]() , oricare ar fi
, oricare ar fi ![]() (inegalitatea
triunghiului).
(inegalitatea
triunghiului).
![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() .
.
Functia ![]() , care verifica numai axiomele 2) si 3) se
numeste seminorma pe
, care verifica numai axiomele 2) si 3) se
numeste seminorma pe ![]() .
.
3. Observatie. Daca alegem ![]() ,
, ![]() , atunci din axioma 2) obtinem
, atunci din axioma 2) obtinem ![]() sau (folosind partea a
doua a axiomei 1)) deducem
sau (folosind partea a
doua a axiomei 1)) deducem ![]() , care implica
, care implica ![]() . Cum
. Cum ![]() era ales oarecare,
observam ca axioma 1) nu este independenta (!).
era ales oarecare,
observam ca axioma 1) nu este independenta (!).
Exemple: (i). Fie ![]() un spatiu vectorial si
un spatiu vectorial si ![]() o aplicatie
lineara (vezi, 22). Atunci functia
o aplicatie
lineara (vezi, 22). Atunci functia ![]() , definita prin
, definita prin ![]() ,
, ![]() este o seminorma
pe
este o seminorma
pe ![]() .
.
(ii). Fie ![]() spatiu vectorial
finit dimensional de dimensiune
spatiu vectorial
finit dimensional de dimensiune ![]() ,
, ![]() un vector definit prin
coordonatele sale pe o baza fixata in
un vector definit prin
coordonatele sale pe o baza fixata in ![]() si
si ![]() o aplicatie
lineara. Este posibil sa existe vectori
o aplicatie
lineara. Este posibil sa existe vectori ![]() nenuli a.i.
nenuli a.i. ![]() . Astfel de aplicatii lineare sunt definite printr-o
relatie de forma
. Astfel de aplicatii lineare sunt definite printr-o
relatie de forma ![]() si ele
genereaza in
si ele
genereaza in ![]() un hiperplan:
un hiperplan: ![]() .
.
Acest exemplu arata ca, pe un
spatiu vectorial dat, se pot introduce mai multe norme. Se poate
arata ca toate aceste norme sunt echivalente.
Altfel spus, daca in ![]() sunt definite
doua norme
sunt definite
doua norme ![]() si
si ![]() , atunci exista doua constante pozitive
, atunci exista doua constante pozitive ![]() a.i.
a.i. ![]() .
.
Orice spatiu vectorial normat ![]() poate fi metrizat, daca definim distanta intre orice doua
puncte
poate fi metrizat, daca definim distanta intre orice doua
puncte ![]() prin,
prin,
![]() . (1)
. (1)
4.
Definitie. Fie ![]() un spatiu vectorial normat. Spatiul
un spatiu vectorial normat. Spatiul ![]() se numeste spatiu Banach
daca si numai daca este complet
in raport cu metrica (1).
se numeste spatiu Banach
daca si numai daca este complet
in raport cu metrica (1).
(Reamintim ca spatiul
metric ![]() se numeste
complet daca si numai daca orice sir Cauchy din
se numeste
complet daca si numai daca orice sir Cauchy din ![]() este convergent)
este convergent)
5.
Definitie. Fie ![]() un spatiu
vectorial real. Functia
un spatiu
vectorial real. Functia ![]() , care verifica axiomele:
, care verifica axiomele:
(1) ![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() daca si
numai daca
daca si
numai daca ![]() ,
,
(2) ![]() , oricare ar fi
, oricare ar fi ![]() ,
,
(3) ![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() ,
,
(4) ![]() , oricare ar fi
, oricare ar fi ![]() ,
,
se numeste produs scalar (produs interior) pe ![]() .
.
6. Observatie. Axioma a doua arata linearitatea produsului scalar in raport cu prima componenta, iar axioma 4) exprima conditia de simetrie. Pe baza axiomeloe 2) si 4) deducem linearitatea produsului scalar in a doua componenta, altfel spus,
![]() , oricare ar fi
, oricare ar fi ![]() . (2)
. (2)
Observatie. In cazul cand ![]() este spatiu vectorial complex atunci
axioma (4) se inlocueste cu axioma
este spatiu vectorial complex atunci
axioma (4) se inlocueste cu axioma
(4'). ![]() , oricare ar fi
, oricare ar fi ![]() .
.
(Bara asezata
deasupra numarului complex ![]() arata conjugatul
acestui numar complex).
arata conjugatul
acestui numar complex).
Definitie. Un spatiu vectorial finit dimensional ![]() real (sau complex) pe
care s-a definit un produs scalar se numeste spatiu vectorial euclidian. Daca spatiul vectorial
real (sau complex) pe
care s-a definit un produs scalar se numeste spatiu vectorial euclidian. Daca spatiul vectorial ![]() este complex adesea,
folosim denumirea de spatiuvectorial
unitar.
este complex adesea,
folosim denumirea de spatiuvectorial
unitar.
9.
Propozitie. Fie ![]() un spatiu
vectorial real (sau complex) inzestrat cu un produs scalar, notat
un spatiu
vectorial real (sau complex) inzestrat cu un produs scalar, notat ![]() . Atunci functia
. Atunci functia ![]() ,
, ![]() , defineste o norma
pe
, defineste o norma
pe ![]() ,
,
![]() , (3)
, (3)
(numita norma asociata produsului scalar) si aceasta norma verifica inegalitatea lui Cauchy-Schwarz
![]() , oricare ar fi
, oricare ar fi ![]() . (4)
. (4)
Demonstratie. Avem ![]() echivalenta cu
echivalenta cu ![]() , care implica
, care implica ![]() .
.
![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() .
.
Din prima axioma a produsului scalar
deducem ![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() . Mai departe, avem
. Mai departe, avem ![]() , oricare ar fi
, oricare ar fi ![]() . Daca punem
. Daca punem ![]() , atunci ultima relatie devine
, atunci ultima relatie devine ![]() ,
, ![]() , de unde rezulta
, de unde rezulta
![]() si inegalitatea
(4) este verificata.
si inegalitatea
(4) este verificata.
Utilizand inegalitatea lui Schwarz, deducem
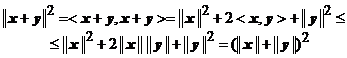
si atunci avem ![]() .
.
Exemplu. Vom considera spatiul vectorial real ![]() , in raport cu adunarea obisnuita si
inmultirea cu scalari, avand dimensiunea egala cu
, in raport cu adunarea obisnuita si
inmultirea cu scalari, avand dimensiunea egala cu ![]() . Precizam ca multimea
. Precizam ca multimea
![]() ,
,
unde ![]() , formeaza baza
canonica in
, formeaza baza
canonica in ![]() .
.
Atunci pentru orice element ![]() ,
, ![]() , avem
, avem ![]() .
.
Norma unui element (vector) ![]() , este definita prin
, este definita prin
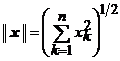 . (5)
. (5)
Pentru orice doi vectori ![]() si
si ![]() din
din ![]() , functia
, functia
![]() , (6)
, (6)
defineste un produs scalar pe ![]() .
.
Fie ![]() un spatiu
vectorial complex de dimensiune finita
un spatiu
vectorial complex de dimensiune finita ![]() , in care s-a precizat o baza si vectorii
, in care s-a precizat o baza si vectorii ![]() si
si ![]() din
din ![]() . Atunci functia
. Atunci functia
![]() , (6')
, (6')
defineste un produs scalar
pe ![]() . (Daca
. (Daca ![]() , atunci
, atunci ![]() este conjugatul complex al lui
este conjugatul complex al lui ![]() ).
).
10.
Definitie. Fie ![]() un spatiu
vectorial. Submultimea
un spatiu
vectorial. Submultimea ![]() se numeste subspatiu vectorial al lui
se numeste subspatiu vectorial al lui ![]() daca
verifica conditiile;
daca
verifica conditiile;
i). ![]() este multime
inchisa.
este multime
inchisa.
ii daca ![]() , atunci
, atunci ![]() .
.
iii). daca ![]() si
si ![]() , atunci
, atunci ![]() .
.
Fie ![]() un spatiu
vectorial. Multimea
un spatiu
vectorial. Multimea ![]() se numeste convexa daca odata cu
orice doua puncte
se numeste convexa daca odata cu
orice doua puncte ![]() , aceasta multime contine si segmentul
, aceasta multime contine si segmentul
![]() ,
,
care uneste aceste puncte.
In spatiul vectorial normat ![]() , bula de centru
, bula de centru ![]() avand raza
avand raza ![]() ,
,
![]() , (7)
, (7)
este o multime convexa.
11.
Definitie. Fie ![]() o submultime
convexa a spatiului vectorial
o submultime
convexa a spatiului vectorial ![]() . Functia
. Functia ![]() se numeste convexa (respectiv concava) daca pentru orice
se numeste convexa (respectiv concava) daca pentru orice ![]() si orice
si orice ![]() are loc inegalitatea
are loc inegalitatea
![]() , (8)
, (8)
(respectiv, ![]() ).
).
Functia ![]() se numeste strict convexa (respectiv strict concava) daca pentru
orice
se numeste strict convexa (respectiv strict concava) daca pentru
orice ![]() si orice
si orice ![]() are loc inegalitatea
stricta
are loc inegalitatea
stricta
![]() (8')
(8')
(respectiv,![]() ).
).
Din definitie rezulta ca
functia ![]() este convexa daca functia
este convexa daca functia ![]() este concava.
este concava.
Functia ![]() se numeste afina pe
se numeste afina pe ![]() daca este in
acelasi timp concava si convexa pe
daca este in
acelasi timp concava si convexa pe ![]() .
.
12. Observatie. (1). Daca ![]() sau
sau ![]() , atunci inegalitatile devin egalitati.
, atunci inegalitatile devin egalitati.
(2). Norma ![]() ,
, ![]() spatiu vectorial,
este o functie convexa.
spatiu vectorial,
este o functie convexa.
(3). Fie ![]() un interval deschis,
un interval deschis, ![]() o functie de
clasa
o functie de
clasa ![]() . Daca
. Daca ![]() , atunci
, atunci ![]() este convexa pe
este convexa pe ![]() ; daca
; daca ![]() , atunci
, atunci ![]() este concava pe
este concava pe ![]() .
.
13. Observatie. Proprietatea din definitia functiilor convexe poate fi exprimata prin relatiile echivalente:
![]() si oricare ar fi
si oricare ar fi ![]() sa avem
sa avem
![]() .
.
Spatii Hilbert
14. Un spatiu vectorial
real ![]() in care s-a definit un
produs scalar
in care s-a definit un
produs scalar ![]() , normat cu norma asociata de produsul scalar,
, normat cu norma asociata de produsul scalar, ![]() , se numeste spatiu
prehilbertian. Daca acest spatiu este complet (spatiu
Banach), el se numeste spatiu
Hilbert.
, se numeste spatiu
prehilbertian. Daca acest spatiu este complet (spatiu
Banach), el se numeste spatiu
Hilbert.
Exercitiul
1. Fie ![]() un spatiu
vectorial. Daca
un spatiu
vectorial. Daca ![]() este norma
asociata unui produs scalar atunci are loc identitatea paralelogramului
este norma
asociata unui produs scalar atunci are loc identitatea paralelogramului
![]() , oricare ar fi
, oricare ar fi ![]() . (9)
. (9)
Reciproc, daca o norma pe
spatiul vectorial ![]() verifica identitatea paralelogramului atunci
exista un produs scalar pe
verifica identitatea paralelogramului atunci
exista un produs scalar pe ![]() a carui
norma asociata coincide cu norma data.
a carui
norma asociata coincide cu norma data.
Intr-adevar, fie ![]() , un spatiu vectorial real normat a.i. norma
verifica relatia (9). Daca definim
, un spatiu vectorial real normat a.i. norma
verifica relatia (9). Daca definim
![]() , oricare ar fi
, oricare ar fi ![]() , (10)
, (10)
se verifica imediat ca functia ![]() este un produs scalar
pe
este un produs scalar
pe ![]() si avem
si avem ![]() .
.
In cazul cand ![]() este un spatiu
vectorial complex normat a.i. norma verifica relatia (1) atunci
este un spatiu
vectorial complex normat a.i. norma verifica relatia (1) atunci
![]() , oricare ar fi
, oricare ar fi ![]() , (2')
, (2')
defineste un produs scalar pe ![]() .
.
15. Observatie.
Pe spatiul ![]() exista norme care
nu pot genera un produs scalar.
exista norme care
nu pot genera un produs scalar.
De exemplu, norma definita prin
![]() , oricare ar fi
, oricare ar fi ![]() . (11)
. (11)
nu verifica identitatea paralelogramului si deci nu poate fi asociata unui produs scalar.
Intr-adevar, daca alegem ![]() si
si ![]() , atunci avem
, atunci avem
![]()
si evident nu are loc identitatea paralelogramului.
16. Observatie. Conceptele de linear dependenta a unei multimi finite si de dimensiune finita a unui spatiu sunt pur algebrice; pentru definirea lor folosim numai conceptul de spatiu vectorial.
Daca spatiul vectorial ![]() este izestrat cu un
produs scalar, este posibil sa obtinem un numar de
proprietati utile ale acestui spatiu.
este izestrat cu un
produs scalar, este posibil sa obtinem un numar de
proprietati utile ale acestui spatiu.
(i).
Mai intai sa verificam daca mutimea finita ![]() este linear
independena sau nu. Pentru aceasta, fie combinatia lineara
nula
este linear
independena sau nu. Pentru aceasta, fie combinatia lineara
nula
![]() ,
, ![]() . (12)
. (12)
Inmultind scalar in ambele
parti ale ecuatiei (12), succesiv cu fiecare element ![]() obtinem
obtinem
![]() ,
, ![]() .
.
Cu notatiile, ![]() , ultimele relatii se scriu sub forma
, ultimele relatii se scriu sub forma
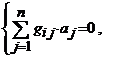
![]() sau
sau ![]() , (13)
, (13)
unde ![]() este matrice
simetrica,
este matrice
simetrica, ![]() este o matrice
coloana. Conditia necesara si suficienta ca sistemul
linear si omogen (13) sa aiba solutie nebanala este ca
este o matrice
coloana. Conditia necesara si suficienta ca sistemul
linear si omogen (13) sa aiba solutie nebanala este ca
![]() ; deci multimea
; deci multimea ![]() este linear dependenta daca si numai daca
este linear dependenta daca si numai daca
![]() .
.
Exemplu. Fie ![]() spatiul
functiilor continue definite pe intervalul
spatiul
functiilor continue definite pe intervalul ![]() cu valori reale.
Definim produsul scalar al functiilor
cu valori reale.
Definim produsul scalar al functiilor ![]() prin
prin
![]() .
.
Atunci multimea functiilor ![]() este linear independenta in
este linear independenta in ![]() .
.
Intr-adevar, punand
![]() ,
,
avem
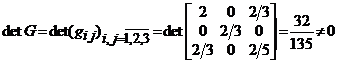 .
.
(ii). Vom defini multimile ortonormale si bazele intr-un spatiu vectorial.
1
Definitie. Fie ![]() un spatiu Hilbert
(eventual prehilbertian). Vom spune ca elementele (vectorii)
un spatiu Hilbert
(eventual prehilbertian). Vom spune ca elementele (vectorii) ![]() sunt ortogonale daca
sunt ortogonale daca ![]() si scriem
si scriem ![]() . Multimea finita
. Multimea finita ![]() se numeste ortonormala daca si numai
daca
se numeste ortonormala daca si numai
daca
![]() .
.
(Altfel spus, elementele
multimii ![]() sunt ortogonale
doua cate doua si au lungimea egala cu
sunt ortogonale
doua cate doua si au lungimea egala cu ![]() .
.
Orice multime ortonormala este linear independenta.
Intr-adevar, daca folosim
relatiile (13), deducem ca matricea ![]() (
(![]() este matricea unitate).
este matricea unitate).
Presupunem ca ![]() este un spatiu
finit dimensional cu
este un spatiu
finit dimensional cu ![]() . Atunci o baza care verifica conditiile
definitiei (17) se numeste baza
ortonormala. De exemplu, in
. Atunci o baza care verifica conditiile
definitiei (17) se numeste baza
ortonormala. De exemplu, in ![]() , multimea (finita)
, multimea (finita)
![]() ,
,
formeaza o baza ortonormala, in raport cu produsul scalar (6).
Unul din avantajele folosirii bazelor
ortonormale este acela ca multe calcule complicate, efectuate in alte
baze, se fac mult mai usor in bazele ortonormale si formulele
obtinute se scriu mai simplu. De exemplu, daca ![]() este o baza
ortonormala in spatiul vectorial
este o baza
ortonormala in spatiul vectorial ![]() si
si ![]() , atunci
, atunci
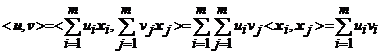 .
.
Data fiind o baza oarecare (care nu
este ortonormala) ![]() , este posibil totdeauna, folosind procedeul de ortonormalizare Gram-Schmidt, sa construim o
baza ortonormala.
, este posibil totdeauna, folosind procedeul de ortonormalizare Gram-Schmidt, sa construim o
baza ortonormala.
Pentru orice ![]() , numerele
, numerele ![]() se numesc coeficientii Fourier ai lui
se numesc coeficientii Fourier ai lui ![]() in raport cu sistemul
ortonormal
in raport cu sistemul
ortonormal ![]() .
.
Exercitiul
2. (Aproximarea in medie patratica). Fie ![]() un spatiu
prehilbertian. Daca
un spatiu
prehilbertian. Daca ![]() sunt coeficientii Fourier ai lui
sunt coeficientii Fourier ai lui ![]() , in raport cu sistemul ortonormal
, in raport cu sistemul ortonormal ![]() , atunci are loc inegalitatea
lui Bessel:
, atunci are loc inegalitatea
lui Bessel:
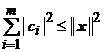 . (14)
. (14)
Intr-adevar, putem scrie
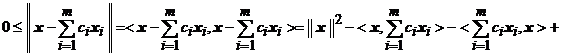
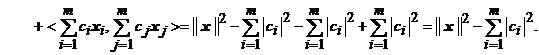
Exercitiul 2) poate fi
interpretat astfel: dintre toate combinatiile lineare de forma ![]() , cea mai buna
aproximare in sensul normei din
, cea mai buna
aproximare in sensul normei din ![]() (
(![]() poate fi chiar
poate fi chiar ![]() ) a unui element
) a unui element ![]() este realizata de
combinatia lineara in care coeficientii
este realizata de
combinatia lineara in care coeficientii ![]() sunt egali cu
coeficientii Fourier
sunt egali cu
coeficientii Fourier ![]() asociati lui
asociati lui ![]() (vezi seminarul).
(vezi seminarul).
1 Observatie.
Consideratiile de mai inainte se pot extinde la o multime oarecare de
elemente din spatiul prehilbertian ![]() . Multimea
. Multimea ![]() este, prin
definitie, ortonormala
daca elementele acestei multimi sunt ortogonale doua cate
doua si au norma egala cu
este, prin
definitie, ortonormala
daca elementele acestei multimi sunt ortogonale doua cate
doua si au norma egala cu ![]() .
.
Exemplu. Notam cu ![]() clasa functiilor
reale definite pe intervalul
clasa functiilor
reale definite pe intervalul ![]() , de patrat integrabile. Altfel spus,
, de patrat integrabile. Altfel spus, ![]() daca si
numai daca
daca si
numai daca ![]() apartine unei
clase de echivalenta de functii de patrat integrabile
(adica, verifica conditiile):
apartine unei
clase de echivalenta de functii de patrat integrabile
(adica, verifica conditiile):
1). ![]() este integrabila;
este integrabila;
2). ![]() este integrabila,
este integrabila,
![]() ;
;
3). functiile ![]() si
si ![]() sunt echivalente (vom
scrie
sunt echivalente (vom
scrie ![]() )
) 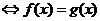 a.p.t. pe
a.p.t. pe ![]() .
.
Aceasta multime, in care s-a
definit adunarea functiilor ![]() si inmultirea cu scalari
si inmultirea cu scalari ![]() , oricare ar fi
, oricare ar fi ![]() si
si ![]() , prin
, prin
![]() si
si ![]() ,
, ![]() ,
,
formeaza un spatiu vectorial real. Pe acest spatu vectorial introducem norma
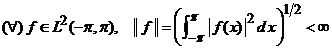 . (15)
. (15)
Pe spatiul vectorial real ![]() , definim produsul scalar
, definim produsul scalar
![]() . (16)
. (16)
Asadar, spatiul vectorial real ![]() este un spatiu
prehilbertian.
este un spatiu
prehilbertian.
Sirul de functii ![]() cu
cu ![]() este convergent in norma daca
exista o functie
este convergent in norma daca
exista o functie ![]() a.i. sirul de
numere reale
a.i. sirul de
numere reale ![]() converge catre
zero, cand
converge catre
zero, cand ![]() :
:
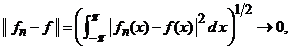 cand
cand ![]() . (17)
. (17)
In acest caz spunem ca sirul de
functii ![]() din
din ![]() converge in medie patratica, pe intervalul
converge in medie patratica, pe intervalul ![]() , la functia
, la functia ![]() .
.
Daca sirul de functii ![]() converge in medie patratica in
converge in medie patratica in ![]() la functia
la functia ![]() nu rezulta
ca
nu rezulta
ca ![]() tinde catre
tinde catre ![]() in fiecare punct
in fiecare punct ![]() . De exemplu, sirul de functii
. De exemplu, sirul de functii
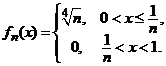
tinde in medie patratica pe
intervalul ![]() catre
functia nula, dar nu converge uniform pe acest interval.
catre
functia nula, dar nu converge uniform pe acest interval.
Intr-adevar, din
![]() implica
implica ![]() ,
,
ceea ce arata ca sirul ![]() converge in medie
patratica catre functia nula. Analizand
convergenta in sensul distantei dintre
converge in medie
patratica catre functia nula. Analizand
convergenta in sensul distantei dintre ![]() si functia
nula,
si functia
nula,
![]() , cand
, cand ![]() ,
,
deducem ca sirul nu converge uniform.
19. Observatie.
Daca sirul ![]() converge uniform pe
intervalul
converge uniform pe
intervalul ![]() catre
functia
catre
functia ![]() atunci el converge in
medie patratica. Intr-adevar, fie
atunci el converge in
medie patratica. Intr-adevar, fie ![]() , fixat. Datorita ipotezei, putem alege
, fixat. Datorita ipotezei, putem alege ![]() suficient de mare a.i.
suficient de mare a.i.
![]() . Atunci avem
. Atunci avem
![]() ,
,
ceea ce arata convergenta in ![]() .
.
Asa dupa cum s-a aratat , reciproc nu este adevarat.
20.
Propozitie. Daca
sirul de functii ![]() din
din ![]() converge in medie patratica la functia
converge in medie patratica la functia ![]() , atunci pentru orice functie
, atunci pentru orice functie ![]() , sirul de produse scalare
, sirul de produse scalare ![]() (definit de (16))
converge catre
(definit de (16))
converge catre ![]() .
.
Demonstratie. Pentru a demonstra aceasta
afirmatie este suficient sa aratam ca sirul ![]() tinde la zero.
Folosind inegalitatea lui Schwarz,
tinde la zero.
Folosind inegalitatea lui Schwarz,
![]() ,
,
si deoarece, ![]() , cand
, cand ![]() , deducem ca
, deducem ca ![]() .
.
21. Observatie. Se poate demonstra ca ![]() , cu norma (15), este spatiu vectorial real normat complet. Spatiul
functiilor continue
, cu norma (15), este spatiu vectorial real normat complet. Spatiul
functiilor continue ![]() este dens in
este dens in ![]() . In
. In ![]() norma (15) este
generata de produsul scalar (16) si deci
norma (15) este
generata de produsul scalar (16) si deci ![]() este un spatiu Hilbert.
este un spatiu Hilbert.
Exercitiul 3. Multimea functiilor
![]() , (18)
, (18)
formeaza un sistem ortogonal
pe intervalul![]() in raport cu produsul scalar (16), iar
in raport cu produsul scalar (16), iar
![]() , (19)
, (19)
este o multime ortonormala
de functii pe intervalul ![]() .
.
22. Pentru orice functia![]() asociem seria Fourier
trigonometrica (generata de functia
asociem seria Fourier
trigonometrica (generata de functia![]() )
)
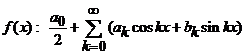 , (20)
, (20)
unde
![]() (21)
(21)
se numesc coeficientii
Fourier[2]
asociati functiei ![]() in raport cu sistemul
ortogonal (18).
in raport cu sistemul
ortogonal (18).
Convergenta seriei Fourier trigonometrice (20), generata de functia ![]() , este inteleasa in medie patratica, adica in sensul normei din
, este inteleasa in medie patratica, adica in sensul normei din ![]() , definita prin relatia (15). Mai precis, fie polinomul trigonometric
, definita prin relatia (15). Mai precis, fie polinomul trigonometric
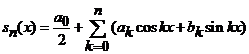 , (22)
, (22)
care reprezinta sirul
sumelor partiale asociat seriei (22), atunci aceasta serie
converge catre functia ![]() daca si
numai daca sirul numeric
daca si
numai daca sirul numeric ![]() converge la zero:
converge la zero:
![]() . (23)
. (23)
23.
Definitie. Functia
![]() este periodica
de perioada
este periodica
de perioada
![]() , daca
, daca
![]() .
.
24. Observatie.
Daca functia ![]() este periodica de
perioada
este periodica de
perioada ![]() , atunci
, atunci ![]() verifica
conditia
verifica
conditia
![]() .
.
Daca, in plus, ![]() este integrabila
pe
este integrabila
pe ![]() , atunci
, atunci
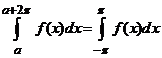 , oricare ar fi
, oricare ar fi ![]() .
.
Analog, ca mai inainte, pentru orice
functie ![]() , periodica cu perioada
, periodica cu perioada ![]() , continua pe portiuni pe orice interval compact,
asociem seria Fourier trigonometrica (generata de
functia
, continua pe portiuni pe orice interval compact,
asociem seria Fourier trigonometrica (generata de
functia![]() )
)
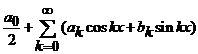 , (24)
, (24)
unde
![]() (25)
(25)
se numesc
coeficientii Fourier asociati functiei ![]() in raport cu sistemul
ortogonal (18).
in raport cu sistemul
ortogonal (18).
25.
Teorema. (Dirichlet). Fie![]() o functie periodica cu perioada
o functie periodica cu perioada ![]() care verifica
conditiile:
care verifica
conditiile:
(1). ![]() este continua pe
portiuni.
este continua pe
portiuni.
(2). derivata ![]() este continua pe
portiuni,
este continua pe
portiuni,
atunci seria Fourier trigonometrica
asociata lui ![]() converge in orice
punct de continuitate
converge in orice
punct de continuitate ![]() catre
functia
catre
functia ![]() si avem,
si avem,
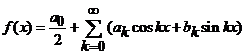 , (26)
, (26)
iar in
orice punct de discontinuitate ![]() seria este
convergenta si suma seriei este egala cu saltul lui
seria este
convergenta si suma seriei este egala cu saltul lui ![]() in acest punct:
in acest punct:
![]() . (27)
. (27)
Aplicatii lineare
Aplicatiile lineare au sens daca sunt definite pe spatii lineare (normate). Aplicatiile lineare, de exemplu, functionalele lineare si formele bilineare joaca un rol important in studiul problemelor initiale si la limita; operatorii de proiectie sunt legati de aproximarea problemelor initiale si la limita; un rol important il au operatorii lineari pe spatii vectoriale finit dimensionale, de exemplu, in numeroase situatii se aproximeaza o functie (aplicatie) cu o aplicatie lineara.
26.
Definitie. Fie ![]() doua spatii
vectoriale normate, reale. O aplicatie
doua spatii
vectoriale normate, reale. O aplicatie ![]() se numeste lineara daca verifica
proprietatile:
se numeste lineara daca verifica
proprietatile:
1). ![]() (proprietatea de aditivitate),
(proprietatea de aditivitate),
2). ![]() (proprietatea de omogenitate),
(proprietatea de omogenitate),
pentru orice ![]() si orice
si orice ![]() .
.
Fie ![]() spatii vectoriale
reale. Vom nota cu
spatii vectoriale
reale. Vom nota cu ![]() multimea tuturor
aplicatiilor lineare definite pe
multimea tuturor
aplicatiilor lineare definite pe ![]() cu valori in
cu valori in ![]()
O aplicatie lineara a unui spatiu in el insusi se numeste operator linear (sau endomorfism), iar daca aplicatia lineara este definita pe un spatiu vectorial cu valori reale se numeste adesea, functionala lineara.
Endomorfismele de spatii vectoriale finit dimensionale sunt marginite, deci continue.
Exemplul
1. Fie ![]() ,
, ![]() si
si ![]() multimea
aplicatiilor lineare si continue definite pe
multimea
aplicatiilor lineare si continue definite pe ![]() cu valori in
cu valori in ![]() si
si ![]() o aplicatie
lineara si continua. Atunci pentru orice
o aplicatie
lineara si continua. Atunci pentru orice ![]() (
(![]() este scalar, deoarece orice vector din
este scalar, deoarece orice vector din ![]() este scalar (!)) avem
este scalar (!)) avem
![]()
unde ![]() este un scalar unic determinat.
este un scalar unic determinat.
Aceasta relatie
arata structura aplicatiilor lineare de la ![]() in
in ![]() . Altfel spus, data fiind aplicatia lineara
si continua
. Altfel spus, data fiind aplicatia lineara
si continua ![]() , atunci exista unic scalarul (
, atunci exista unic scalarul (![]() a.i.
a.i. ![]() . Scalarul
. Scalarul ![]() este unic determinat
de valoarea lui
este unic determinat
de valoarea lui ![]() pe o baza a
spatiului vectorial
pe o baza a
spatiului vectorial ![]() .
.
2
Definitie. Fie ![]() si
si ![]() doua spatii
vectoriale normate. O aplicatie
doua spatii
vectoriale normate. O aplicatie ![]() se numeste
izometrie de spatii vectoriale daca
se numeste
izometrie de spatii vectoriale daca
Aplicatia ![]() este lineara
si bijectiva
este lineara
si bijectiva
Oricare
ar fi ![]() , (aplicatia
, (aplicatia ![]() pastreaza
norma).
pastreaza
norma).
2
Propozitie. Fie ![]() spatii vectoriale
normate, reale. O aplicatie lineara
spatii vectoriale
normate, reale. O aplicatie lineara ![]() , continua intr-un punct
, continua intr-un punct ![]() , este continua in tot spatiul
, este continua in tot spatiul ![]() .
.
Demonstratie. Fie ![]() un punct oarecare al
spatiului
un punct oarecare al
spatiului ![]() . Functia
. Functia ![]() , definita prin,
, definita prin, ![]() este o izometrie a lui
este o izometrie a lui ![]() in el insusi.
Intr-adevar, functia
in el insusi.
Intr-adevar, functia ![]() este bijectiva
si invariaza distanta intre orice doua puncte din
este bijectiva
si invariaza distanta intre orice doua puncte din ![]() :
: ![]() , avem
, avem
![]()
Fie bula ![]() . Atunci
. Atunci ![]() si deci
si deci ![]() transforma
transforma ![]() in bula
in bula ![]() si reciproc. Fie
si reciproc. Fie ![]() oarecare, dar fixat.
Atunci, din continuitatea lui
oarecare, dar fixat.
Atunci, din continuitatea lui ![]() in
in ![]() , rezulta ca exista
, rezulta ca exista ![]() astfel incat orice
astfel incat orice ![]() avem
avem ![]() . Cum
. Cum ![]() este lineara avem
este lineara avem
![]()
si deci ![]() .
.
Deoarece ![]() , atunci din
, atunci din ![]() rezulta
rezulta
![]() ,
,
ceea ce arata
continuitatea lui ![]() in
in ![]() .
.
29.
Teorema. Fie ![]() un spatiu
vectorial normat de dimensiune finita si
un spatiu
vectorial normat de dimensiune finita si ![]() un spatiu normat
oarecare. Atunci orice aplicatie lineara
un spatiu normat
oarecare. Atunci orice aplicatie lineara ![]() este uniform
continua. Mai mult, exista
este uniform
continua. Mai mult, exista ![]() a.i.
a.i.
![]() oricare ar fi
oricare ar fi ![]() . (28)
. (28)
Demonstratie. Fie ![]() si
si ![]() o baza in
spatiul
o baza in
spatiul ![]() . Atunci, orice
. Atunci, orice ![]() poate fi scris unic
sub forma
poate fi scris unic
sub forma ![]() ,
, ![]() . Daca punem
. Daca punem
![]() ,
,
obtinem o norma pe ![]() . Deoarece orice doua norme definite pe un spatiu
vectorial finit dimensional sunt echivalente, deducem ca norma
introdusa este echivalenta cu
. Deoarece orice doua norme definite pe un spatiu
vectorial finit dimensional sunt echivalente, deducem ca norma
introdusa este echivalenta cu ![]() , adica exista
, adica exista ![]() a.i.
a.i. ![]() . Asadar, folosind linearitatea lui
. Asadar, folosind linearitatea lui ![]() putem scrie
putem scrie
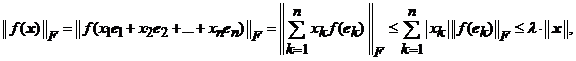
unde 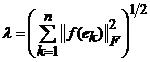 . Cu notatia
. Cu notatia ![]() obtinem inegalitatea
(28).
obtinem inegalitatea
(28).
Uniform continuitatea aplicatiei lineare
![]() rezulta imediat
din (28) deoarece pentru orice
rezulta imediat
din (28) deoarece pentru orice ![]() avem
avem ![]() .
.
30.
Definitie. Fie ![]() si
si ![]() doua spatii
vectoriale normate (nu obligatoriu finit dimensionale). O aplicatie
lineara
doua spatii
vectoriale normate (nu obligatoriu finit dimensionale). O aplicatie
lineara ![]() este marginita daca
exista
este marginita daca
exista ![]() (
(![]() depinde de
depinde de ![]() si nu depinde de
si nu depinde de ![]() ) a.i.
) a.i.
![]() oricare ar fi
oricare ar fi ![]() . (29)
. (29)
Inegalitatea (29) permite definirea normei unui operator: Fie ![]() . Aplicatia
. Aplicatia ![]() , definita prin
, definita prin
![]() (30)
(30)
este o norma pe
spatul vectorial ![]() , numita norma
operatorului
, numita norma
operatorului ![]() si atunci pentru
orice aplicatie lineara
si continua deci marginita, putem scrie
inegalitatea fundamentala
si atunci pentru
orice aplicatie lineara
si continua deci marginita, putem scrie
inegalitatea fundamentala
![]() oricare ar fi
oricare ar fi ![]() . (31)
. (31)
Intr-adevar, daca ![]() , inegalitatea este verificata. Daca
, inegalitatea este verificata. Daca ![]() , atunci relatia (29) poate fi scrisa sub forma
, atunci relatia (29) poate fi scrisa sub forma ![]() . Asadar, este natural ca cel mai mic majorant al lui
. Asadar, este natural ca cel mai mic majorant al lui ![]() , care verifica inegalitatea (29), sa fie numit
norma operatorului
, care verifica inegalitatea (29), sa fie numit
norma operatorului ![]() si notat prin
si notat prin ![]() . In consecinta, punem
. In consecinta, punem ![]() si avem (31). Pe
de alta parte, daca
si avem (31). Pe
de alta parte, daca ![]() atunci
atunci ![]() . Fie
. Fie ![]() , atunci
, atunci ![]() si din
inegalitatea (31) obtinem
si din
inegalitatea (31) obtinem ![]() . Daca
. Daca ![]() , atunci avem
, atunci avem ![]() . Asadar,
. Asadar, ![]() este cel mai mic
numar dintre toate numerele
este cel mai mic
numar dintre toate numerele ![]() cu proprietatea
data de formula (29). ramane de aratat ca functia care defineste "norma lui
cu proprietatea
data de formula (29). ramane de aratat ca functia care defineste "norma lui ![]() ",
", ![]() , data de (30), verifica axiomele normei (vezi
teorema 32).
, data de (30), verifica axiomele normei (vezi
teorema 32).
Exemplul
2. Fie ![]() , definita prin
, definita prin ![]() ,
, ![]() . Folosind norma convergentei uniforme,
. Folosind norma convergentei uniforme, ![]() , sa se arate ca operatorul linear
, sa se arate ca operatorul linear ![]() este marginit.
este marginit.
Indicatie. Din ![]() ,
,
deducem ![]() si in
consecinta, operatorul linear
si in
consecinta, operatorul linear ![]() este marginit,
prin urmare continuu.
este marginit,
prin urmare continuu.
31. Teorema. Fie ![]() si
si ![]() spatii
vectoriale normate (nu neaparat de dimensiune finita). O aplicatie lineara
spatii
vectoriale normate (nu neaparat de dimensiune finita). O aplicatie lineara ![]() este continua daca
si numai daca este marginita.
este continua daca
si numai daca este marginita.
Demonstratie. Aratam implicatia "![]() " Vom presupune ca aplicatia lineara este
marginita si fie
" Vom presupune ca aplicatia lineara este
marginita si fie ![]() ,
, ![]() . Avem
. Avem
![]() ,
,
de unde rezulta chiar uniform continuitatea lui ![]() .
.
Aratam implicatia in sens invers " ![]() " Fie
" Fie ![]() o aplicatie
lineara continua despre care presupunem ca nu este
marginita. Atunci pentru orice
o aplicatie
lineara continua despre care presupunem ca nu este
marginita. Atunci pentru orice ![]() exista un
sir
exista un
sir ![]() din spatiul
vectorial
din spatiul
vectorial ![]() a.i.
a.i. ![]() sau
sau ![]() . Folosind proprietatile normei si faptul
ca
. Folosind proprietatile normei si faptul
ca ![]() este o aplicatie lineara avem
este o aplicatie lineara avem 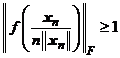 . Fie sirul
. Fie sirul ![]() . Deoarece
. Deoarece ![]() , atunci avem
, atunci avem ![]() . Din relatia
. Din relatia ![]() deducem ca
deducem ca ![]() si deci, aplicatia
lineara nu este continua in origine si ipoteza este
contrazisa.
si deci, aplicatia
lineara nu este continua in origine si ipoteza este
contrazisa.
In continuare vom prezenta si alte
definitii ale normei unei
aplicatii lineare ![]() .
.
32. Teorema. Fie ![]() si
si ![]() spatii
vectoriale normate finit dimensionale.
Pentru orice aplicatie lineara si marginita
spatii
vectoriale normate finit dimensionale.
Pentru orice aplicatie lineara si marginita ![]() avem
avem
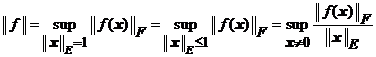 . (*)
. (*)
In acest caz spunem ca ![]() este o norma de
aplicatie lineara subordonata
normei vectoriale
este o norma de
aplicatie lineara subordonata
normei vectoriale ![]() din
din ![]() .
.
Demonstratie. Existenta numarului ![]() apare din teorema 29
si formula (29), daca se alege
apare din teorema 29
si formula (29), daca se alege ![]() . In adevar, daca notam
. In adevar, daca notam ![]() si cum
si cum ![]() , oricare ar fi
, oricare ar fi ![]() ; punand
; punand ![]() deducem ca
deducem ca ![]() si cum
si cum ![]() este finit avem
este finit avem ![]() .
.
Fie ![]() . Aratam ca oricare din formulele (*) definesc
o norma:
. Aratam ca oricare din formulele (*) definesc
o norma:
Avem evident, ![]() si
si ![]() in orice punct din
in orice punct din ![]() . Intr-adevar,
. Intr-adevar,
![]()
![]()
![]()
![]()
si deci pentru orice ![]() avem
avem ![]() (operatorul linear
nul).
(operatorul linear
nul).
2) Fie ![]() . Atunci
. Atunci
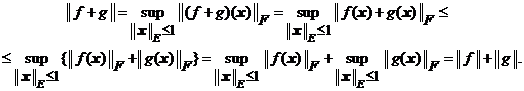
3) Fie ![]() si
si ![]() atunci avem
atunci avem
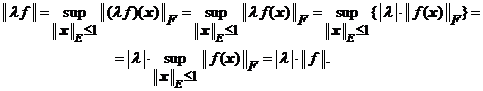
Din inegalitatea
fundamentala (31) deducem ca daca ![]() atunci
atunci 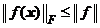 , si deci
, si deci
![]() . (**)
. (**)
Din definitia lui ![]() rezulta ca
pentru orice
rezulta ca
pentru orice ![]() , fixat, exista un punct
, fixat, exista un punct ![]() a.i. sa avem
a.i. sa avem
![]() .
.
Daca punem ![]() , atunci
, atunci ![]() si avem
si avem
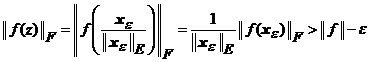 ,
,
de unde, cu atat mai mult ![]() . Deoarece
. Deoarece ![]() a fost ales arbitrar,
deducem
a fost ales arbitrar,
deducem
![]() . Tinand seama de
inegalitatile (**) rezulta egalitatile (*). Mai mult, avem
. Tinand seama de
inegalitatile (**) rezulta egalitatile (*). Mai mult, avem
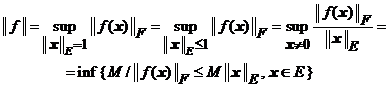 .
.
Exemplul
3. Fie ![]() si
si ![]() . Fie
. Fie ![]() multimea
aplicatiilor lineare si continue definite pe
multimea
aplicatiilor lineare si continue definite pe ![]() cu valori in
cu valori in ![]() , si fie
, si fie ![]() o aplicatie
lineara si continua. Atunci pentru orice
o aplicatie
lineara si continua. Atunci pentru orice ![]() (
(![]() este scalar, deoarece orice vector din
este scalar, deoarece orice vector din ![]() este scalar(!)) avem
este scalar(!)) avem
![]() , (32)
, (32)
unde vectorul ![]() este unic determinat.
este unic determinat.
Aceasta relatie arata
structura aplicatiilor lineare de la ![]() in
in ![]() . Altfel spus, dat fiind aplicatia lineara si
continua
. Altfel spus, dat fiind aplicatia lineara si
continua ![]() , atunci exista unic vectorul
, atunci exista unic vectorul ![]() a.i.
a.i. ![]() . Vectorul
. Vectorul ![]() este unic determinat
de valoarea lui
este unic determinat
de valoarea lui ![]() pe o baza a lui
pe o baza a lui ![]() . Operatorul
. Operatorul ![]() este marginit
si pentru orice
este marginit
si pentru orice
![]() , avem
, avem 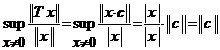 . Deci
. Deci ![]() .
.
Aratam ca ![]() este izomorf cu
este izomorf cu ![]() . In acest scop, definim aplicatia
. In acest scop, definim aplicatia ![]() , prin
, prin
![]() .
.
Constatam ca aplicatia ![]() este lineara:
este lineara: ![]() .
.
Aplicatia ![]() este injectiva
si cum este aplicatie lineara pe spatii finit dimensionale
este si surjectiva, deci
este injectiva
si cum este aplicatie lineara pe spatii finit dimensionale
este si surjectiva, deci ![]() este bijectiva.
Deoarece
este bijectiva.
Deoarece
![]() ,
,
deducem ca ![]() pastreaza
norma, deci este o izometrie. Aceasta izometrie ne permite sa
identificam spatiul Banach
pastreaza
norma, deci este o izometrie. Aceasta izometrie ne permite sa
identificam spatiul Banach ![]() cu
cu ![]() .
.
Exemplul 4. Fie ![]() si
si ![]() si ca de obicei,
notam cu
si ca de obicei,
notam cu ![]() spatiul vectorial
al aplicatiilor lineare si continue definite pe
spatiul vectorial
al aplicatiilor lineare si continue definite pe ![]() cu valori in
cu valori in ![]() , si fie
, si fie ![]() o aplicatie
lineara si continua. Atunci exista o unica matrice
o aplicatie
lineara si continua. Atunci exista o unica matrice ![]() (matricea
(matricea ![]() , cu
, cu ![]() linii si
linii si ![]() coloane este matricea asociata operatorului
linear
coloane este matricea asociata operatorului
linear ![]() pe bazele canonice ale
spatiilor
pe bazele canonice ale
spatiilor ![]() si
si ![]() ) a.i.
) a.i.
![]()
![]() , (33)
, (33)
unde ![]() este matricea
coloana formata cu coordonatele vectorului
este matricea
coloana formata cu coordonatele vectorului ![]() .
.
Daca ![]() , atunci
, atunci ![]() . Vom nota cu
. Vom nota cu 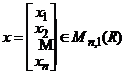 si
si 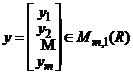 , matricele care au pe coloana coordonatele vectorilor
, matricele care au pe coloana coordonatele vectorilor ![]() respectiv,
respectiv, ![]() . Atunci relatia (33) se scrie matricial
. Atunci relatia (33) se scrie matricial
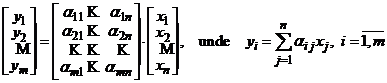 . (34)
. (34)
Fiind data aplicatia 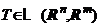 , atunci matricea
, atunci matricea ![]() , care verifica formula (33) sau (34) este unica
si se numeste matricea
asociata operatorului linear
, care verifica formula (33) sau (34) este unica
si se numeste matricea
asociata operatorului linear ![]() calculata pe
bazele canonice ale spatiilor
calculata pe
bazele canonice ale spatiilor ![]() si
si ![]() (vezi observatia 35).
(vezi observatia 35).
Operatorul ![]() este marginit
si norma sa este data de norma matricei asociata
este marginit
si norma sa este data de norma matricei asociata ![]() .
.
Intr-adevar, fie ![]() . Datorita teoremei 32, daca alegem pe cele
doua spatii vectoriale
. Datorita teoremei 32, daca alegem pe cele
doua spatii vectoriale ![]() si
si ![]() aceeasi
norma, de exemplu,
aceeasi
norma, de exemplu, ![]() , atunci norma operatorului linear
, atunci norma operatorului linear ![]() subordonata
acestei norme vectoriale este egala cu norma matricei
subordonata
acestei norme vectoriale este egala cu norma matricei ![]() :
:
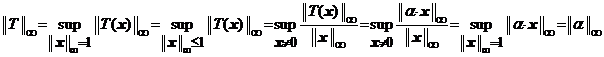 .
.
Folosind relatia (34), obtinem
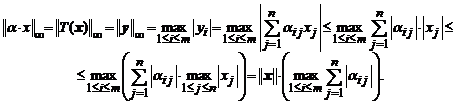
Atunci, are loc majorarea
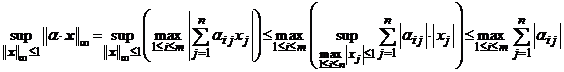
care arata ca operatorul ![]() este marginit.
este marginit.
Deoarece ![]() este functie
continua pe
este functie
continua pe ![]() si multimea
si multimea ![]() este compacta,
atunci marginea superioara poate fi atinsa si in
consecinta, putem defini norma matricei
este compacta,
atunci marginea superioara poate fi atinsa si in
consecinta, putem defini norma matricei ![]() (norma operatorului
(norma operatorului ![]() ) subordonata normei vectoriale
) subordonata normei vectoriale ![]() , prin
, prin
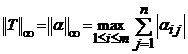 . (35)
. (35)
De exemplu, daca alegem vectorul ![]() , atunci
, atunci ![]() si observam
ca marginea superioara poate fi atinsa in acest punct:
si observam
ca marginea superioara poate fi atinsa in acest punct:
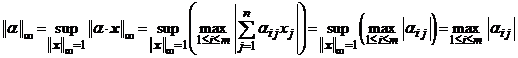 .
.
33. Observatie.
Daca pe ![]() alegem norma
alegem norma ![]() , atunci se poate arata ca norma asociata
operatorului
, atunci se poate arata ca norma asociata
operatorului ![]() subordonata
normei vectoriale
subordonata
normei vectoriale ![]() are forma
are forma
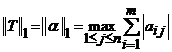 . (36)
. (36)
34. Observatie. Relatiile (33) sau (34) arata structura
aplicatiilor lineare de la ![]() in
in ![]() . Altfel spus, dat fiind aplicatia lineara si
continua
. Altfel spus, dat fiind aplicatia lineara si
continua ![]() , atunci exista o unica matrice asociata lui
, atunci exista o unica matrice asociata lui ![]() care verifica
formula (33) si reciproc. Asadar, spatiul vectorial
care verifica
formula (33) si reciproc. Asadar, spatiul vectorial ![]() este izomorf cu spatiul
vectorial al matricelor cu
este izomorf cu spatiul
vectorial al matricelor cu ![]() linii si
linii si ![]() coloane cu elemente
reale.
coloane cu elemente
reale.
35. Observatie.
(Calculul matricei asociate operatorului
![]() ). Fiind data aplicatia lineara si
continua
). Fiind data aplicatia lineara si
continua ![]() , se cere sa se calculeze matricea asociata lui
, se cere sa se calculeze matricea asociata lui ![]() ,
, ![]() , care verifica formula (33).
, care verifica formula (33).
Fie ![]() baza canonica in
baza canonica in ![]() , unde
, unde ![]() . Cum
. Cum ![]() este produsul direct notat
este produsul direct notat ![]() , atunci se poate pune pune in evidenta
componentele operatorului
, atunci se poate pune pune in evidenta
componentele operatorului ![]() ,
, ![]() :
:
![]() , adica
, adica ![]() .
.
Avem ![]() , unde
, unde ![]() reprezinta linia
reprezinta linia ![]() a matricei
a matricei ![]() ;
;
36. Operatorii de derivare permit definirea
aplicatiilor lineare care nu sunt continue. Notam cu ![]() spatiul vectorial
al functiilor reale definite pe
spatiul vectorial
al functiilor reale definite pe ![]() de clasa
de clasa ![]() pe acest interval si cu
pe acest interval si cu ![]() spatiul vectorial
al functiilor reale continue definite pe
spatiul vectorial
al functiilor reale continue definite pe ![]() . Pe aceste spatii consideram norma
convergentei uniforme
. Pe aceste spatii consideram norma
convergentei uniforme ![]() .
.
Fie ![]() operatorul de derivare
operatorul de derivare
![]() , care asociaza la orice functie
, care asociaza la orice functie ![]() , derivata sa
, derivata sa ![]() . Aratam ca acest operator linear(!) nu este continuu.
. Aratam ca acest operator linear(!) nu este continuu.
Fie de exemplu, functia polinomiala
![]() . Atunci
. Atunci ![]() . Pe de alta parte, avem
. Pe de alta parte, avem
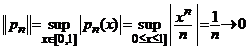 , cand
, cand ![]()
in schimb, ![]() si nu poate
sa tinda catre zero. Asadar, operatorul de derivare nu este
continuu.
si nu poate
sa tinda catre zero. Asadar, operatorul de derivare nu este
continuu.
3 Lema.
Fie ![]() , unde
, unde ![]() si
si ![]() . Daca
. Daca ![]() este matricea
asociata aplicatiei
este matricea
asociata aplicatiei ![]() si
si ![]() este matricea
asociata aplicatiei
este matricea
asociata aplicatiei ![]() atunci matricea produs
atunci matricea produs![]() este matricea asociata aplicatiei
este matricea asociata aplicatiei ![]() .
.
Demonstratie. Deoarece ![]() este matricea
asociata aplicatiei
este matricea
asociata aplicatiei ![]() atunci, potrivit
formulei (31), putem scrie
atunci, potrivit
formulei (31), putem scrie ![]() . Asemanator, din faptul ca
. Asemanator, din faptul ca ![]() este matricea
asociata aplicatiei
este matricea
asociata aplicatiei ![]() , atunci
, atunci ![]() . Din
. Din
![]() ,
,
de unde rezulta ca ![]() este matricea
asociata aplicatiei
este matricea
asociata aplicatiei ![]() . Mai mult, deoarece
. Mai mult, deoarece ![]() si
si ![]() sunt matrice unic
determinate, atunci matricea
sunt matrice unic
determinate, atunci matricea ![]() exista si
este unica.
exista si
este unica.
3 Observatie.
Fie ![]() ,
, ![]() atunci
atunci ![]() bijectiva
daca si numai daca
bijectiva
daca si numai daca ![]() si matricea
asociata
si matricea
asociata ![]() este inversabila.
este inversabila.
"![]() ". Presupunem ca
". Presupunem ca ![]() este bijectiv. Atunci
este bijectiv. Atunci ![]() si exista o
unica aplicatie
si exista o
unica aplicatie ![]() a. i.
a. i. ![]() si
si ![]() . Fie
. Fie ![]() matricea asociata
lui
matricea asociata
lui ![]() si
si ![]() matricea asociata
lui
matricea asociata
lui ![]() .
.
Din definitia aplicatiei identice, ![]()
![]() , rezulta egalitatea
, rezulta egalitatea ![]() si deci, matricea asociata aplicatiei
identice
si deci, matricea asociata aplicatiei
identice ![]() , este matricea unitate
, este matricea unitate
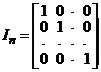 . Avem
. Avem ![]() si
si ![]() , deci
, deci ![]() .
.
S. Banach (1892-1945), distins matematician polonez, avand importante rezultate in teoria spatiilor linear normate.
Joseph Jean-Baptiste Fourier (1768-1830), matematician francez, membru al Academiei de Stiinte din Paris. In Théorie analytique de la chaleur (1882) studiaza fenomenul de propagare a caldurii prin difuzie. Numele sau este legat de marea descoperire matematica, seriile trigonometrice, numite serii Fourier.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |