
Sa se determine multimea punctelor
din plan ale caror afixe ![]() satisfac:
satisfac:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() .
.
Sa se determine forma trigonometrica a urmatoarelor numere complexe:
a) ![]() e)
e) ![]()
b) ![]() f)
f) ![]()
c) 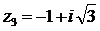 g)
g) ![]()
d) ![]() h)
h) ![]()
Fie ![]() un numar real
nenul. Sa se arate ca forma trigonometrica a lui
un numar real
nenul. Sa se arate ca forma trigonometrica a lui ![]() este:
este:
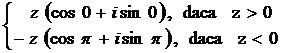
Fie ![]() un numar complex
nenul. Sa se arate ca:
un numar complex
nenul. Sa se arate ca:
![]()
Sa se determine modulele si argumentele numerelor:
a) ![]()
b) ![]()
c) ![]()
d) ![]() ,
, ![]() .
.
Sa se calculeze
produsul ![]() sub forma
trigonometrica
sub forma
trigonometrica
Sa se calculeze modulele si argumentele reduse ale urmatoarelor numere
complexe:
a) ![]() d)
d) ![]()
b) 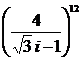 e )
e ) 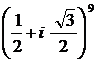
c) 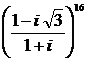 f)
f) ![]()
Sa se calculeze:
a) ![]() ; b)
; b) 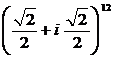 ; c)
; c) ![]() ,
, ![]() ,
, ![]() .
.
Sa se arate
ca, daca numerele naturale ![]() si
si ![]() sunt prime intre ele,
atunci ecuatiile
sunt prime intre ele,
atunci ecuatiile ![]() si
si ![]() au o singura
radacina comuna.
au o singura
radacina comuna.
Sa se rezolve urmatoarele ecuatii binome:
a) ![]() c)
c) ![]()
b) ![]() d)
d) ![]() .
.
Sa se rezolve ecuatiile:
a) ![]() c)
c) ![]()
b) ![]() d)
d) ![]() .
.
5.5 Sa se reprezinte multimile punctelor din plan ale caror afixe satisfac:
a) ![]() d)
d) ![]()
b) ![]() e)
e) ![]() .
.
c) ![]()
a) Stiind ca
![]() ,
, ![]() , sa se calculeze
, sa se calculeze ![]() .
.
b)
Sa se calculeze ![]() , stiind ca
, stiind ca ![]() .
.
Sa se demonstreze
ca formula lui Moivre este adevarata si in cazul in care ![]() este un numar
intreg negativ.
este un numar
intreg negativ.
Sa se
demonstreze: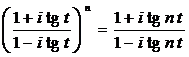 , unde:
, unde: ![]()
![]() .
.
Sa se efectueze calculele:
a) 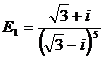 ; b)
; b) ![]() .
.
Fie expresia ![]() . Sa se calculeze
. Sa se calculeze ![]() .
.
Exercitii:
Sa se calculeze
radacinile de ordin ![]() ale lui
ale lui ![]() in urmatoarele
cazuri:
in urmatoarele
cazuri:
a) ![]() c)
c) ![]()
b) ![]() d)
d) ![]() .
.
Sa se determine radacinile de ordin 3, 4 si 8 ale unitatii.
Sa se demonstreze
ca radacinile de ordin ![]() ale unitatii
sunt egale cu puterile unei radacini particulare
ale unitatii
sunt egale cu puterile unei radacini particulare ![]() ( o astfel de
radacina se numeste radacina primi-tiva de
ordin
( o astfel de
radacina se numeste radacina primi-tiva de
ordin ![]() al unitatii
).
al unitatii
).
![]() ,
, ![]() ,
, ![]() fiind
radacinile de ordin 3 ale unitatii, sa se arate
ca:
fiind
radacinile de ordin 3 ale unitatii, sa se arate
ca:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
Stiind ca
numarul complex ![]() verifica
ecuattia
verifica
ecuattia ![]() , sa se arate ca nume-rele
, sa se arate ca nume-rele ![]() ,
, ![]() si
si ![]() verifica
aceeasi ecuatie.
verifica
aceeasi ecuatie.
Aplicatie:
Sa se calculeze ![]() si sa se
deduca radacinile de ordinul 4 ale numarului
si sa se
deduca radacinile de ordinul 4 ale numarului ![]() .
.
Sa se verifice
pozitia celui de-al treilea varf al triunghiului echilateral, afixele a 2
varfuri fiind: ![]() ,
, ![]() .
.
Fie ![]() trei numere complexe,
nenule, distincte 2 cate 2 si de module egale. Sa se demonstreze
ca daca
trei numere complexe,
nenule, distincte 2 cate 2 si de module egale. Sa se demonstreze
ca daca ![]() ,
, ![]() si
si ![]() sunt numere reale,
atunci
sunt numere reale,
atunci ![]() .
.
Notand cu ![]() multimea radacinilor de ordinul
multimea radacinilor de ordinul ![]() ale
unitatii,
ale
unitatii, ![]()
sa se demonstreze ca:
a) ![]() ; b)
; b) ![]()
Sa se determine
numerele complexe de modul 1 care verifica 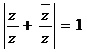 .
.
Fie ecuatia ![]() ,
, ![]() si
si ![]() si
si ![]() . Sa se arate ca ecuatia data are cel
putin o radacina de modul egal cu 1.
. Sa se arate ca ecuatia data are cel
putin o radacina de modul egal cu 1.
Fie ![]() trei numere complexe
nenule, astfel incat
trei numere complexe
nenule, astfel incat ![]() .
.
a)
Sa se demonstreze ca ![]() numerele complexe
numerele complexe ![]() si
si ![]() astfel incat
astfel incat ![]() ,
, ![]() si
si ![]()
b)
Sa se rezolve ecuatia ![]() in raport cu una din
necunoscute.
in raport cu una din
necunoscute.
c)
Folosind eventual rezultatele de la a) si b) sa se demonstreze
ca daca ![]() atunci
atunci ![]() sau numerele
sau numerele ![]() sunt varfurile unui
triunghi echilateral.
sunt varfurile unui
triunghi echilateral.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |