
Caracteristicile numerice ale unei variabile aleatoare continue.
Consideram ca si in cazul unei variabile aleatoare discreta, caracteristicile numerice ale unei variabile aleatoare continui x de densitate de probabilitate f(x).
Definitia 1. Se numeste speranta matematica o variabila aleatoare continua x de densitate de probabilitate f(x) expresia:
M[x] = ![]() (VII 55)
(VII 55)
Daca variabila
aleatoare ![]() nu poate sa ia
valori decat in intervalul finit [a, b], speranta matematica M[x]
este data de formula:
nu poate sa ia
valori decat in intervalul finit [a, b], speranta matematica M[x]
este data de formula:
M[x] = 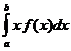 (VII 55' )
(VII 55' )
Se poate considera formula (VII 55' ) ca o generalizare a formulei cunoscuta
deja
M[x] = ![]() (VII 56)
(VII 56)
Intr-adevar descompunem segmentul [a, b] in intervalele (xk-1 , xk).
Alegem un punct ![]() in fiecare din aceste
intervale. Consideram variabila aleatoare discreta auxiliara
in fiecare din aceste
intervale. Consideram variabila aleatoare discreta auxiliara ![]() , care poate sa ia valorile:
, care poate sa ia valorile:
![]() ,
, ![]() , ....,
, ...., ![]() , ...
, ... ![]()
Presupunem ca probabilitatea valorilor corespunzatoare ale variabilei aleatoare discrete sa fie:
p1 , p2 ,..., pk ,..... pn
p1 = f(![]() )
)![]() ; p2 = f(
; p2 = f(![]() )
)![]() , .., pk =
f(
, .., pk =
f(![]() )
)![]() , ... , pn = f(
, ... , pn = f(![]() )
)![]()
f(![]() )
)![]() este probabilitatea ca variabila aleatoare continua x
sa ia o valoare apartinand intervalului (xk-1 , xk ). Speranta
matematica a variabilei aleatoare discrete
este probabilitatea ca variabila aleatoare continua x
sa ia o valoare apartinand intervalului (xk-1 , xk ). Speranta
matematica a variabilei aleatoare discrete ![]() , va fi:
, va fi:
M[![]() ] =
] = ![]()
sau:
M[![]() ] =
] = ![]() f(
f(![]() )
)![]() +
+ ![]() f(
f(![]() )
)![]() + ...+
+ ...+ ![]() f(
f(![]() )
)![]() + ...
+ ...
..+ ![]() f(
f(![]() )
)![]() =
= ![]()
Trecem la limita cand notam ![]() vom obtine:
vom obtine:
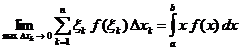
Expresia membrului doi este speranta matematica a variabilei aleatoare continue x, care poate sa ia orice valoare x apartinand segmentului [a, b].
Rationamentul poate fi reluat in mod analog pentru intervalul infinit, adica pentru expresia (VII 55). Adica formulele (VII 55) si (VII 55') sunt analoage lui (VII 56'). Pentru speranta matematica vom utiliza de asemenea notatia mx.
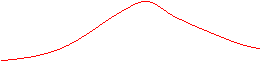
Se numeste speranta matematica centrul de distributie a probabilitatilor variabilei aleatoare x, (Fig.11).
y
![]()
Fig. 11
![]()
![]()
![]() 0 mx x
0 mx x
![]()
 f(x)
f(x)
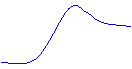
Fig. 12
![]() 0
0
Daca curba de distributie este simetrica in raport cu axa Oy, altfel spus, daca functia f(x) este para, atunci este evident ca:
M[![]() ] =
] = 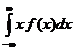 = 0
= 0
In acest caz centrul de distributie coincide cu originea coordonatelor (Fig.12). Consideram variabila aleatoare centrala x- mx. Vom gasi speranta sa matematica:
M[![]() - mx] =
- mx] = 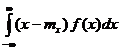 =
= 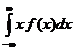 - mx
- mx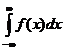
= mx - mx * 1 = 0
Speranta matematica a unei variabile aleatoare centrale este nula.
Definitia
2. Se numeste varianta a
variabilei aleatoare ![]() speranta
matematica a patratului variabilei aleatoare centrate
corespunzatoare:
speranta
matematica a patratului variabilei aleatoare centrate
corespunzatoare:
D[![]() ] =
] = 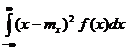 (VII 57)
(VII 57)
Formula (VII 57) este analoaga formulei:
D[x] = ![]()
Definitia 3. Se numeste abatere patratica medie a variabilei aleatoare x radacina patratica a variantei:
s [![]() ] =
] = ![]() =
= ![]()
Aceasta formula este analoaga cu formula:
s[x] = 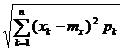
Varianta si abaterea patratica medie caracterizeaza dispersia valorilor variabilei aleatoare.
Definitia 4. Valoarea variabilei aleatoare x, pentru care densitatea de probabilitate admite valoarea sa cea mai mare, se numeste mod si este notata cu M0. Pentru variabila aleatoare x a carei curba de densitate este reprezentata in figurile 11 si 12, modul coincide cu speranta matematica.
Definitia 5. Se numeste "mediana" si notam cu Me numarul care verifica egalitatea:
![]() =
= 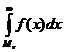 =
= ![]()
![]()
![]()
![]() Aceasta ultima egalitate
Aceasta ultima egalitate
poate fi pusa sub forma:
![]() Me
Me
P(![]() < Me) = P(Me <
< Me) = P(Me < ![]() ) =
) = ![]()
altfel spus este de asemenea probabil ca variabila aleatoare x sa ia o valoare inferioara sau superioara lui Me.
Notam ca variabila aleatoare x poate sa nu admita pe Me ca valoare posibila.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |