Procese de nastere si de moarte. Aplicatii
Se numeste proces de
nastere si de moarte un proces Markov omogen ![]() , cu spatiul
starilor
, cu spatiul
starilor ![]() , care verifica urmatoarele axiome:
, care verifica urmatoarele axiome:
Daca,
la momentul ![]() , procesul se
gaseste in starea
, procesul se
gaseste in starea ![]() , probabilitatea ca la momentul
, probabilitatea ca la momentul ![]() sa se afle
in starea
sa se afle
in starea ![]() este
este ![]() , unde
, unde ![]() ,
, ![]() sunt constante strict pozitive date; deci
sunt constante strict pozitive date; deci ![]() .
.
Daca,
la momentul ![]() , procesul se
gaseste in starea
, procesul se
gaseste in starea ![]() , probabilitatea ca la momentul
, probabilitatea ca la momentul ![]() sa se afle
in starea
sa se afle
in starea ![]() este
este ![]() , unde
, unde ![]() ,
, ![]() sunt constante strict pozitive date; deci
sunt constante strict pozitive date; deci ![]() .
.
Daca,
la momentul ![]() , procesul se
gaseste in starea
, procesul se
gaseste in starea ![]() , probabilitatea ca la momentul
, probabilitatea ca la momentul ![]() sa se afle tot
in starea
sa se afle tot
in starea ![]() este
este ![]() ; deci
; deci ![]() .
.
Probabilitatea
ca in intervalul ![]() sa aiba loc
mai multe treceri dintr-o stare in alta sau sa aiba loc o
trecere diferita de cele descrise la (1),(2) si (3) este
sa aiba loc
mai multe treceri dintr-o stare in alta sau sa aiba loc o
trecere diferita de cele descrise la (1),(2) si (3) este ![]() ; deci
; deci ![]() .
.
Se deduce ca matricea intensitatilor de trecere este:
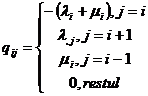
De aici rezulta ecuatiile Kolmogorov inverse:
![]() ,
, ![]()
![]() ,
, ![]()
si ecuatiile Kolmogorov directe:
![]() ,
, ![]()
![]() ,
, ![]()
Solutiile se pot obtine utilizand transformate Laplace.
Evident probabilitatile absolute verifica:
![]() ,
, ![]()
![]()
Daca la momentul ![]() , procesul se gaseste in starea
, procesul se gaseste in starea ![]() , atunci aceste ecuatii se rezolva cu conditia initiala
, atunci aceste ecuatii se rezolva cu conditia initiala ![]() .
.
Daca se noteaza:
![]()
![]() ,
, ![]()
atunci ![]() este o repartitie
stationara. Mai mult, daca
este o repartitie
stationara. Mai mult, daca ![]() avem:
avem:
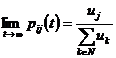 .
.
Un caz particular important
al procesului de nastere si moarte este procesul liniar de
nastere si moarte (procesul Feeler-Arley) pentru care ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Sa consideram functia generatoare:
![]()
Atunci se deduce:
![]()
Solutia generala a acestei ecuatii este
![]()
unde ![]() este o functie arbitrara de clasa
este o functie arbitrara de clasa ![]() . Daca
. Daca ![]() , atunci
, atunci ![]() , adica
, adica ![]() si, prin urmare
si, prin urmare ![]() . Deci:
. Deci:
![]()
Dupa dezvoltarea
in serie de puteri a functiei ![]() dupa puterile lui
s, se obtine, pentru
dupa puterile lui
s, se obtine, pentru ![]() :
:
![]() ,
, ![]()
![]()
unde:
![]()
![]()
Tot cu ajutorul functiei generatoare se obtin media si dispersia procesului:
![]()
![]() ,
, ![]()
Un proces de nastere
si de moarte este numit subcritic, critic sau supercritic
dupa cum ![]() ,
, ![]() sau
sau ![]() . Am vazut ca pentru procese subcritice sau
supercritice dispersia este data de reltia de mai sus. Pentru procese
critice:
. Am vazut ca pentru procese subcritice sau
supercritice dispersia este data de reltia de mai sus. Pentru procese
critice: ![]() .
.
Cand ![]() :
:
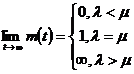
Probabilitatea ca, pentru ![]() procesul sa intre
in starea
procesul sa intre
in starea ![]() (populatia
sa dispara) se obtine din:
(populatia
sa dispara) se obtine din:
![]() , rezulta:
, rezulta:
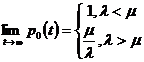
Deci pentru ![]() procesul se
indreapta sigur catre moarte, in timp ce pentru
procesul se
indreapta sigur catre moarte, in timp ce pentru ![]() procesul va
supravietui cu o probabilitate cu atat mai mare cu cat
procesul va
supravietui cu o probabilitate cu atat mai mare cu cat ![]() este mai mare
decat
este mai mare
decat ![]() .
.
Utilizari
Functionarea unui sistem format din n elemente identice care
functioneaza independent in paralel poate fi descrisa de
un proces de nastere si moarte. Starea ![]() semnifica faptul
ca sunt defecte
semnifica faptul
ca sunt defecte ![]() din cele n elemente. În acest caz
din cele n elemente. În acest caz ![]() , pentru
, pentru ![]() si ,
si ,![]() pentru
pentru![]() .
.
Se considera functia matriciala: 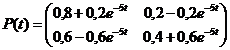 .
.
a).- Sa se arate ca P(t) este o functie matriciala de trecere!
O matrice de trecere este o matrice de functii cu proprietatile:
![]() care se verifica si in cazul nostru;
care se verifica si in cazul nostru;
![]() care se verifica
si in cazul nostru:
care se verifica
si in cazul nostru:
![]()
![]()
![]() unde
unde ![]() este simbolul lui
Kronecker.
este simbolul lui
Kronecker.
În cazul nostru avem:
![]()
![]()
![]()
![]()
Deoarece toate aceste conditii sunt indeplinite P(t) este o matrice de trecere.
b).- Fie ![]() procesul Markov
corespunzator cu spatiul starilor
procesul Markov
corespunzator cu spatiul starilor ![]() . Pentru
. Pentru ![]() ;
; ![]() ;
; ![]() , sa se calculeze
, sa se calculeze
![]()
Am privit aceasta probabilitate ca
probabilitatea ca ![]() si
si ![]() si
si ![]() daca
daca ![]() . Deci evident, cu notatiile:
. Deci evident, cu notatiile:
![]()
![]()
![]()
![]()
vom avea: ![]() si:
si:
![]()
![]()
![]()
rezulta: P
Se
considera un lant Markov ![]() , cu spatiul starilor
, cu spatiul starilor ![]() si matricea de
trecere
si matricea de
trecere
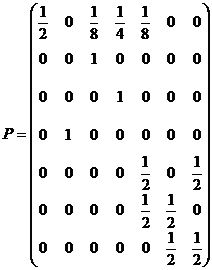
a).- Sa se traseze graful asociat si sa se precizeze starile recurente si cele tranziente.
Toate starile sunt tranziente!
b).- Sa se calculeze
probabilitatile ![]() - probabilitatea ca lantul sa ajunga
vreodata in
- probabilitatea ca lantul sa ajunga
vreodata in ![]() daca, la momentul
daca, la momentul
![]() a fost in starea
a fost in starea ![]() .
.
![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]()
![]() sau
sau ![]()
![]()
Similar, luand toate drumurile prin care se poate ajunge dintr-un punct in altul, cu probabilitatile pentru fiecare pas, rezulta:
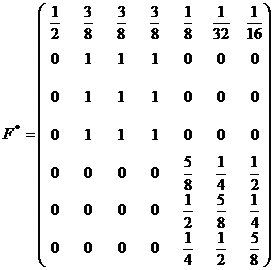
Se considera procesul stationar in sens larg in sens
larg ![]() si fie
si fie ![]() ,
, ![]() , functia de covarianta. Sa se calculeze
, functia de covarianta. Sa se calculeze ![]() .
.
Stiind ca ![]()
![]()
Rezulta ![]()
Si stiind ca ![]()
Iar procesul este stationar in sens larg, deci ![]() nu depinde de t,
rezulta
nu depinde de t,
rezulta
![]()
Daca procesul ![]() este stationar
in sens larg, atunci functia sa de covarianta,
este stationar
in sens larg, atunci functia sa de covarianta, ![]() , verifica relatia:
, verifica relatia: ![]() pentru orice
pentru orice ![]() .
.
Deoarece procesul este stationar in sens larg :
![]()
deci prin adaugare si substragere :
![]()
Din inegalitatea lui Cebasev:
![]()
Dar din definitia variantei:
![]()
Dar bazandu-ne pe proprietatea de aditivitate a mediei si pe faptul ca procesul este stationar in sens larg:
![]()
Deci:
![]()
care (vezi problema anterioara) este:
![]()
Cumuland toate aceste rezultate:
![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |