
PROBLEME DE GEOMETRIE REZOLVATE COMPARATIV: VECTORIAL SI CLASIC
1. Pe laturile AB, AC (sau pe prelungirile acestora) se iau punctele M si N astfel incat BM = CN. Dreapta care uneste mijloacele segmentelor MN si BC, Q si E este paralela cu bisectoarea unghiului BAC.
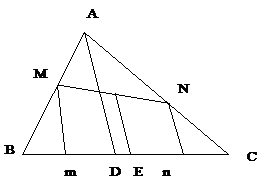
Solutie vectoriala
![]()
![]() , deoarece
, deoarece ![]()
![]()
Deci QE este
paralela cu bisectoarea lui ![]()
Solutie geometrica

Ducem segmentele ![]() , BR
CS MN
, BR
CS MN
Din cele doua paralelograme formate rezulta QR = QS
Dar si BRCS este paralelogram ; diagonalele sale RS si BC se taie in E. In triunghiul isoscel QRS, E este la mijlocul bazei RS , deci QE este si bisectoarea unghiului RQS. Unghiurile BAC, RQS avand laturile paralele, au si bisectoarele paralele.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |