
Definitie. O functie L : A ) cu proprietatea ca L(x,x) = 0 se numeste functie de pierdere. Semnificatia valorii L(x,y) este :"ce pierd daca inlocuiesc valoarea corecta x cu valoarea y ". Din acest punct de vedere este natural sa postulam ca functiile h a L(x,x+h) si h a L(x,x- h) sunt crescatoare in h
Exemple. 1. L(x,y) = x-y p, p > 0. Cazul p = 2 se numeste "functie de pierdere patratica".
2. L(x,y) = ehx-ehy p cu p > 0, h >
3. L(x,y) = (x - y)2ehx cu h >
Definitie. Fie L o functie de pierdere si X 0 o variabila aleatoare (un risc). Numarul AL(X) care minimizeaza functia f(t) = E(L(X,t)) se numeste L- aproximantul lui X. Intuitiv: daca am inlocui variabila aleatoare cu constanta AL(X) pierderea medie ar fi minima. Nu intotdeauna un asemenea numar existasau, daca exista, nu intotdeauna este unic. Pentru a gasi formule de calcul, este suficient in multe cazuri sa presupunem riscul X marginit.
Exemple. . f(t) = E( X - t p) . Daca p > 1, f este derivabila si f'(t) = pE( X-t p- sign(X-t)). Mai mult, functia f este strict convexa deci are un unic punct de minim. Acesta este solutia ecuatiei
E X-t p- sign(X-t)) = 0.
Numarul AL(X) se
numeste in acest caz p-aproximantul
lui X. Este interesant cazul p = 2: ecuatia (5.1) devine E(X-t) = 0 T t = A2(X) = EX. Deci 2-aproximantul este chiar media
- lucru cunoscut sub numele de "proprietatea de optim a mediei". Cazul p = 1 face exceptie: functia
modul nu este derivabila iar ecuatia (5.1) devenita E(sign(X-t)) = 0 P(X > t) = P(X < t)
s-ar putea sa nu aiba solutii. O analiza directa a
functiei f(t) = E X-t ne arata ca minimul ei se atinge pentru t = Median(X) . Mediana lui X este locul unde functia de repartitie a lui X ia valoarea ½ sau cuantila de 50%. Definitia
se poate da si riguros, vezi cursul general. Daca p < 1
lucrurile se complica deoarece functia f nu mai este convexa, nici derivabila, poate avea mai
multe puncte de minim dupa cum se poate vedea studiind cazul X ![]() , p = ½ ; atunci
, p = ½ ; atunci
f(t) = ![]() are minime locale (nederivabile) in punctele t = xn.
are minime locale (nederivabile) in punctele t = xn.
Acum f(t) = E( ehX-eht p). Notand Y = ehX, u = eht obtinem functia E( Y - u p) . Daca p > 1 atunci solutia ecuatiei (5.1) este u = Ap(ehX) de unde gasim
AL(X) = ![]()
Formula este valabila si daca p = 1. Pentru cazul p = 2 obtinem aproximantul AL(X) = ![]() . Dar acesta este chiar prima exponentiala Hh(X) ! (vezi lectia !). Stim din inegalitatea lui Jensen
ca prima exponentiala este un principiu de calcul realist, deci Hp(X) EX.
Daca p =1 obtinem ceva
legat de mediana. Pentru h mic
obtinem aproximatia Hh(X) ≈
. Dar acesta este chiar prima exponentiala Hh(X) ! (vezi lectia !). Stim din inegalitatea lui Jensen
ca prima exponentiala este un principiu de calcul realist, deci Hp(X) EX.
Daca p =1 obtinem ceva
legat de mediana. Pentru h mic
obtinem aproximatia Hh(X) ≈ 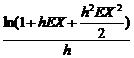 ≈ EX + hEX2/2
≈ EX + hEX2/2
. f(t)
= E((X - t)2ehX) = t2EehX
- 2tE(XehX) . Este o functie de gradul 2, deci tmin = AL(X) = ![]() .
.
Acesta se numeste premiul Esscher calculat cu coeficientul de aversiune la risc h. Pentru valori mici obtinem
neglijind termenii in h2, aproximatia AL(X)
≈ ![]() ≈ (EX + hEX2)(1 - hEX) ≈ EX + hVar(X). Ultimul se foloseste in
actuariat sub numele de premiul variantei.
≈ (EX + hEX2)(1 - hEX) ≈ EX + hVar(X). Ultimul se foloseste in
actuariat sub numele de premiul variantei.
Vom demonstra ca si premiul Esscher este un premiu realist. Ne bazam pe un rezultat mai general, anume
PROPOZITIA 5.1. Fie f,g doua functii avind aceeasi monotonie (sau ambele crescatoare sau ambele descrescatoare) si X o variabila aleatoare cu proprietatea ca variabilele aleatoare f(X), g(X) si f(X)g(X) au medie . Atunci
E(f(X)g(X)) Ef(X) Eg(X)
Demonstratie. Folosim urmatoarea formula a carei verificare o lasam cititorului:
LEMA 5.2. Fie X,Y doua variabile aleatoare i.i.d. si f,g doua functii masurabile cu proprietatea ca variabilele aleatoare f(X), g(X) si f(X)g(X) au medie . Atunci
E[(f(X)- f(Y))(g(X) - g(Y))] = 2[E(f(X)g(X)) - Ef(X) Eg(X)]
Daca f si g au aceeasi monotonie, atunci membrul sting din (5.4) este pozitiv, ceea ce incheie demonstratia. E(f(X)g(X)) Ef(X) Eg(X)
COROLAR 5.3. ![]() EX
EX
Demonstratie. In (5.3) luam f(x) = x si g(x) = ehx
Observatie. Inegalitatea (5.3) are o interpretare foarte naturala: daca f si g au aceeasi monotonie, atunci variabilele aleatoare f(X) si g(X) trebuie sa fie pozitiv corelate! Alta consecinta a inegalitatii ar fi : daca X este o variabila aleatoare pozitiva si a,b > 0 , atunci EXa+b EXaEXb (luam f (x) = xa, g(x) = xb)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |