DEFINITIA 1. Fie E un spatiu
vectorial real cu dim E = n. O aplicatie
F : E
E R se numeste
forma (sau functionala)
biliniara daca
este liniara
in
raport cu ambele argumente, adica
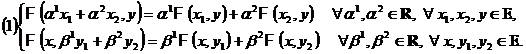
Exemple. 1. Produsul scalar in cazul spatiilor reale este o forma biliniara.
2. Fie 
Rn
si 
, 
vectori
arbitrari din Rn
exprimati in
baza 
. Aplicatia j: EE R definita prin
cu 
constante reale date,
este o forma
biliniara.
Observatia 1. Notiunea
de forma
biliniara
poate fi generalizata in mai multe sensuri.
Daca
E si E
sunt doua
spatii
vectoriale reale, aplicatia F : 
R, de valori F (
), liniara in raport cu ambele
argumente, se numeste forma biliniara.
De
asemenea, daca
E este un spatiu
vectorial complex, aplicatia F : 
C care satisface conditiile (1), in care R se inlocuieste
cu C, iar ultima egalitate cu
F :
F 
F 
, 
fiind conjugatul lui 
se numeste forma biliniara.
In cele ce urmeaza ne vom ocupa numai de forme biliniare precizate in def.1.6.1.
TEOREMA1. Fie o baza
oarecare din E. O forma biliniara F : EE R este complet determinata daca
se cunosc valorile sale F 
pe produsul cartezian BB.
Demonstratie.
Fie 
arbitrari cu
Tinand seama de (1) avem
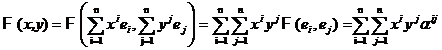
deci
F 
F 
.
DEFINITIA1. Daca este o baza in
E si
F :
R este o forma biliniara,
atunci matricea [
] I M(n, n, R) cu elementele 
F (ei,
ej, i, j = 1, 2, ,n, se numeste matricea formei biliniare F in
baza B.
Notatie. []: = M (F ; 
).
Observatia 1. Sub forma matriceala relatia (2) se poate scrie
F () = [
]tB
M (F ; ) [
]B.
Intr-adevar, avem pe rand
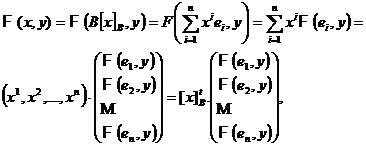
in care,
pentru i = 1, 2, , n, explicitand
pe
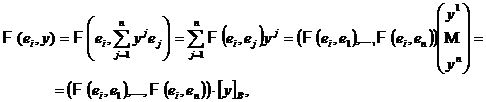
obtinem
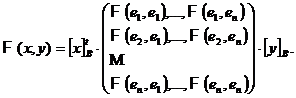
TEOREMA 1. Fie o
forma
biliniara
F : EE R
data
in
baza B si
fie B o alta baza
a spatiului
E. Daca
M(B, B ) este matricea de trecere de
la baza B la baza B , atunci
M(F ; B B ) = M t (B, B M (F ; BB) M(B, B
Demonstratie.
Fie .
Calculand
in
doua
moduri pe F (), tinand seama de relatia (3), obtinem
F () = F (B []B , B []B ) = []tB'
M (F ; B B
[]B
F () = F (B []B , B []B F (B
M (B, B []B , B
M(B, B
[]B
= (M (B, B )
. []B )t M
(F ; BB) M(B, B
[]B
= []tB'
Mt (B, B
M (F ; BB) . M (B, B
[]B .
Folosind proprietatea de tranzitivitate a relatiei de egalitate, rezulta relatia (4).
DEFINITIA 1. Rangul unei forme biliniare este
rangul matricei sale M(F ; BB) = [] intr-o baza B arbitrara in spatiul E.
DEFINITII 1. 1. Forma biliniara F se numeste simetrica daca F () = F (
), I E.
Forma biliniara
F se numeste antisimetrica daca F ()
F (), I E.
TEOREMA 1. (1) O forma biliniara F este simetrica daca si numai daca matricea sa intr-o baza B, arbitrara, este simetrica.
O forma biliniara
F este antisimetrica M (F ; BB) este antisimetrica,
baza B.
Demonstratie.
(1) Fie B o baza arbitrara si
arbitrari. F simetrica F () = F () []tB
M (F ; BB) []B = []tB
M (F ; BB) []B
[]tB
M (F ; BB) []B=( []tB
M (F ; BB) []B)t
M (F ; BB) = Mt (F ; BB).
Se demonstreaza in mod analog cu (1) .
Fie multimea S0(F
PROPRIETATEA 1. Multimea S0(F ) este un subspatiu vectorial al lui E.
Demonstratie.
F (
) =
F (
) + 
F (
) = 0,
I S0(F ) si 
I R, deci 
I S0(F
DEFINITIA 1. S0(F ) se numeste subspatiul nul al formei biliniare F
Observatia 1. Unei forme biliniare F i se asociaza doua subspatii nule, S0(F ) si S'0(F
DEFINITIA 1.6.6. Daca F este o forma biliniara simetrica atunci subspatiul nul (S0(F ) sau S F ) ) se numeste nucleul formei biliniare.
: = Ker (F
VectoriiI E cu proprietatea ca
F () = 0, se numesc vectori
ortogonali in
raport cu F
|
Politica de confidentialitate |
 .com |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
