
Fie En si
baza ![]() .
.
Construim mai intai o baza ortogonala ![]() cu
cu
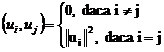
facand urmatoarea consideratie
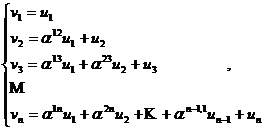 adica cu
adica cu 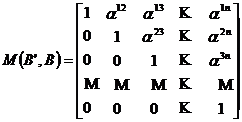 ,
,
matrice superior triunghiulara.
Punand conditia de ortogonalitate a bazei ![]() , obtinem
, obtinem
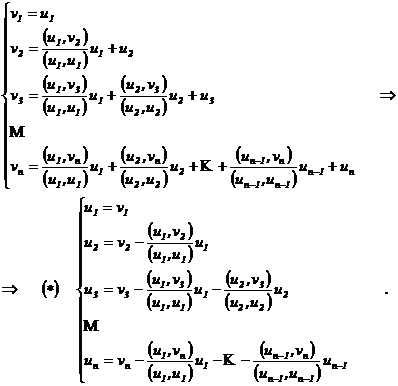
Acest procedeu se numeste Gram-Schmidt.
TEOREMA 1. Fie En.
Daca B=(v1 v2 vn) este o baza a spatiului En , atunci B = (u1 u2 un) de forma ![]() este o baza
ortogonala, iar multimea
este o baza
ortogonala, iar multimea
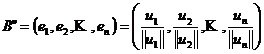
este o baza ortonormata a lui En.
Demonstratie Din constructie
s-a vazut
ca
![]() este o baza
ortogonala
este o baza
ortogonala
![]() baza.
Pentru a demonstra ca
baza.
Pentru a demonstra ca ![]() este ortonormata, consideram produsul
scalar a doi vectori din
este ortonormata, consideram produsul
scalar a doi vectori din ![]()
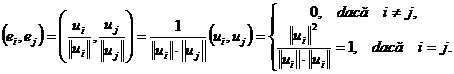
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |