PARTEA INTREAGA A UNUI NUMAR REAL CU O PROPRIETATE MAI PUTIN CUNOSCUTA

Definitia 1.

Functia se numeste functia parte intreaga.

• este cel mai mare numar intreg mai mic decat numarul real . De aici

rezulta ca .

Exemple: ; ; .

Definitia 2.

Functia , se numeste functia parte fractionara.

• ; .

Exemple: ; ; .

Proprietati ale functiei parte intreaga

Proprietatea 1.

;

Altfel scris: .

Proprietatea 2.

, ,

Altfel scris: .

Proprietatea 3.

,

Altfel scris: .

Proprietatea 4.

, ,

Altfel scris: .

In manualele de liceu nu este intalnita proprietatea 3. De aceea, vom demonstra aceasta proprietate, dupa care o vom aplica in rezolvarea unor probleme.

• Demonstrati ca , .

Solutie

Fie ; , .

Distingem doua cazuri: ; .

• I. (1) si (2).

Avem: (3);

(4).

Din (3) deducem: .

• II. (5) si (6).

Avem: (7);

.

Asadar:  ,

Problema 1

Sa se calculeze suma ; .

(O.I.M.-Anglia)

Solutie

Avem S =

.

Problema 2

Rezolvati in R ecuatia

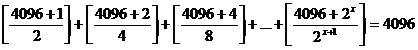, unde reprezinta partea intreaga a numarului real "a".

prof. Adriana Danoiu, Rm. Valcea

Solutie.

.

Bibliografie

1. Matematica, manual pentru clasa a IX-a, C. Nastasescu si altii, Editura Didactica si Pedagogica, R.A., 2005
2. Teme si probleme de matematica, M. Ganga, Editura Tehnica, 1991.