
Paleta neantrenata in miscare de rotatie, avand masa uniform distribuita.
Ipoteze de calcul, (fig.90).
- paleta are aria sectiunii constanta in lungul aerofolie, si nu este torsionata,
- paleta este incastrata la un capat si libera la celalalt capat,
- vibratiile sunt numai de incovoiere,
- centrele de greutate ale sectiunilor coincid cu centrul de greutate al sectiunii de la baza aerofoliei, fiind dispuse pe aceeasi axa.
- sectiunile de incovoiere raman plane si dupa deformatie,
- paleta are o infinitate de puncte materiale, deci si o infinitate de forme de vibratie, respectiv de frecvente proprii.
Pentru calcul se impun conditiile:
- sarcina q, este egala cu forta de inertie Fi, pe unitatea de lungime,
qi = - Fi, respectiv q + Fi = 0. (1)
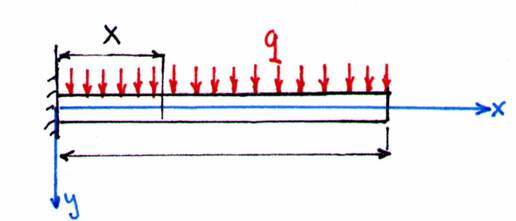
Fig. 90 - Schema de calcul.
Ecuatia fibrei medii deformate este,
![]()
sarcina se obtine din
![]() sau
sau 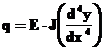 ,
,
forta de inertie Fi pe unitatea de lungime este
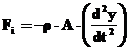
Inlocuind in (l), la echilibru, rezulta,
![]()
sau,
![]() (2)
(2)
se noteaza cu,
![]() (3)
(3)
ca urmare (2) devine,
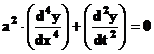 (4)
(4)
Se considera ca paleta vibreaza dupa o lege armonica, de forma:
![]() φ), (5)
φ), (5)
unde,
yn - deformatia pentru armonica n,
y0 - deformatia initiala maxima,
pn - pulsatia armonicii n,
t - timpul,
φ - unghiul de defazare.
Derivata expresiei (5) este,
![]() φ)
φ)
![]() φ)
φ)![]()
Inlocuind in (4), rezulta
![]()
sau
![]()
Se noteaza
![]() (6)
(6)
Ca urmare
![]() (7)
(7)
Ecuatia (7) are solutia:
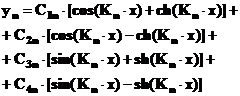 (8)
(8)
C1, C2, C3, C4, sunt constante care se vor determina din conditiile aerofoliei la incastrare si la capatul liber.
La incastrare,
x
= 0, yn = 0, φ =![]()
Introducand in (8), rezulta,
C1n = 0, C3n = 0
La capatul liber,
x = L,
momentul incovoietor este nul,
![]()
si forta taietoare,
![]()
Dar
![]()
![]()
![]()
Sau efectuand derivatele si introducand in (8), se obtine conditia din care se determina parametrul (Kn·L), ca fiind:
![]() (9)
(9)
Pentru paleta fara bandaj la capat, la armonicile 1 ÷ 6, conditia (9) se respecta pentru valorile din tabel:
|
n | ||||||
|
(Kn·L) |
| |||||
|
(Kn·L)2 |
Pentru paleta avand bandaj la capatul liber, valorile sunt:
|
n | |||||
|
(Kn·L) | |||||
|
(Kn·L)2 |
Determinarea pulsatiei se face din (6),
![]()
sau
![]()
Din (3) rezulta
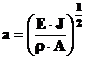
Daca se inmulteste si se imparte cu L2, pulsatia va avea forma:
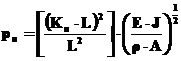 (10)
(10)
iar frecventa va fi
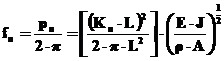 (11)
(11)
Daca in loc de densitatea ρ, se introduce greutatea specifica γ = ρ · g, frecventa va avea expresia:
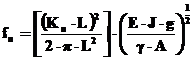 (12)
(12)
Raportul pulsatiilor armonicilor fata de pulsatia proprie fundamentala au valorile din tabel:
|
n | |||||
|
|
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |