
Stabilitatea in sens Lyapunov a sistemelor stohastice inversate
Introducere
In aceasta lucrare trei teoreme referitoare la stabilitatea sistemelor stohastice inversate sunt enuntate si demonstrate. Tehnica Lyapunov este folosita pentru a deriva conditiile suficiente ale sistemelor deosebindu-se cazul functiilor Lyapunov simple si functiile Lyapunov multiple.
Consideratii teoretice
Stabilitatea stohastica Lyapunov
Consideram urmatorul sistem stochastic :
dX(t) = b (X(t)) dt +G(X(t))d![]() (t) (1)
(t) (1)
X(0) = X0
unde X(t) este un
proces dimensional n intamplator , b
(X(t)) dt, G(X(t)) - este un vector si o matrice de ordinul doi intamplatoare ,
respectiv de dimensiuni apropiate, ![]() (t) - este un n standard - proces dimensional "Winer" si X0
un vector de ordinal doi intamplator independent de
(t) - este un n standard - proces dimensional "Winer" si X0
un vector de ordinal doi intamplator independent de ![]() - algebric F (
- algebric F (![]() , T
, T![]() t).
t).
Ecuatia stohastica diferentiala (1) admite
solutia unica X(t) daca exista constantele K1,![]() si
si ![]() .
.
![]()
![]()
Vom analiza stabilitatea
solutiei X(t) =0 a ecuatiei (1), de aceea vom face urmatoarea presupunerea :
b(0) = 0, G(0) = 0. Solutia X(t) a ecuatiei (1) se spune ca este stabila cu probabilitatea t ![]() daca pentru orice s
daca pentru orice s ![]() si
si ![]() >0.
>0.
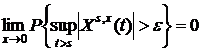 ,
,
unde X![]() este drumul catre solutia ecuatiei (1) incepand din punctul x
la momentul de timp s.
este drumul catre solutia ecuatiei (1) incepand din punctul x
la momentul de timp s.
Teorema 1. Daca U![]() este un domeniu care contine originea si presupunem ca
exista o functie pozitiva definita V : U
este un domeniu care contine originea si presupunem ca
exista o functie pozitiva definita V : U ![]()
![]() , continua diferentiabila cu exceptia originii care satisface
pentru x
, continua diferentiabila cu exceptia originii care satisface
pentru x![]() :
:
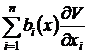 +
+ 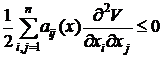
in care a![]() = [GG
= [GG![]() ]
]![]() unde * denota conjugata complexa transformata.
unde * denota conjugata complexa transformata.
Sisteme stohastice inversate
In aceasta lucrare analizam proprietatile stabilitatii a sistemelor stohastice inversate de forma :
dX(t) = b![]() (X(t))dt + G
(X(t))dt + G![]() (X(t))d
(X(t))d![]() (t) (2)
(t) (2)
X(0) = x![]()
unde i ![]() =
= ![]() este un set de indici
al sistemului inversat.
este un set de indici
al sistemului inversat.
Functii Lyapunov simple
Vom face urmatoarea presupunere pentru fiecare
subsistem : b![]() (0) = 0; G
(0) = 0; G![]() (0) = 0 ,
(0) = 0 , ![]() . O functie Lyapunov simpla pentru sistemul (2) este o
functie V : R
. O functie Lyapunov simpla pentru sistemul (2) este o
functie V : R![]()
![]() de doua ori continua diferentiabila cu exceptia originii
care este definita pozitiv V(x) > 0 ,
de doua ori continua diferentiabila cu exceptia originii
care este definita pozitiv V(x) > 0 , ![]() si V(0) = 0 si
proprietatea lim
si V(0) = 0 si
proprietatea lim![]() astfel incat:
astfel incat:
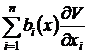 +
+ 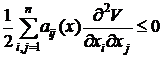
Teorema 2
Daca exista o functie Lyapunov simpla pentru sistemul 2 si toate presupunerile anterioare sunt adevarate atunci sistemul (2) este stabil .
Demonstratie : Pentru fiecare t![]()
![]() rezulta:
rezulta:
V(tj)
= V(tj - 1) + 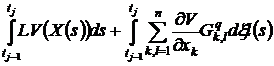
unde q este subsistemul care este activ in intervalul [tj-1, tj].
Folosind faptul ca EV(tj) ![]()
![]() EV(0) = V(x0) in final obtinem :
EV(0) = V(x0) in final obtinem :
P![]() ,
, ![]()
Functii Lyapunov multiple
Facem
urmatoarea presupunere pentru fiecare subsistem (a) b![]() (0) = 0, G
(0) = 0, G![]() (0) = 0,
(0) = 0, ![]() , (b)
, (b) ![]() exista o functie V
exista o functie V![]() de doua ori continua diferentiabila cu exceptia originii
care este definita pozitiv astefel incat V
de doua ori continua diferentiabila cu exceptia originii
care este definita pozitiv astefel incat V![]() si proprietatea lim
si proprietatea lim![]() si (c)
si (c) ![]() , b
, b![]() si G
si G![]() satisface conditia unica (2).
satisface conditia unica (2).
Teorema
3 Daca presupunerile (a), (b) si (c) sunt adevarate , S este setul de
secvente inversate a sistemului. Daca ![]() si
si ![]() urmatoarele conditii
sunt indeplinite:
urmatoarele conditii
sunt indeplinite:
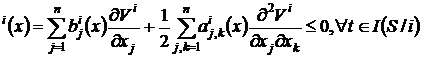
EV![]()
![]()
EV![]()
![]()
Aplicatie la descentralizarea traficului aerian
Fiecare aeronava poate sa aiba informatii estimative cu privire la pozitia curenta a altei aeronave a centrului sau, sau a razei sale, numita "zona de protectie".Principalul motiv al incertitudinii este vantul.
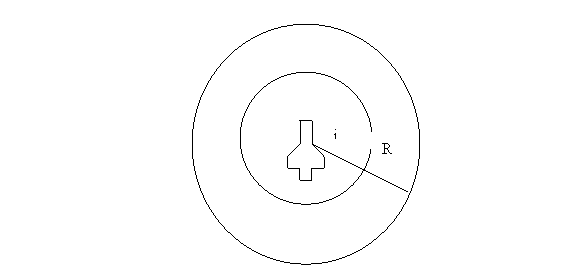
Aeronava i si zona sa de protectie de raza R
Oricand o aeronava intra in zona de protectie a aeronavei i legile de control sunt inversate astfel incat sa intalneasca urmatoarele specificatii:
destinatie convergenta (DC) si evitarea coliziunii (CA).De aici inainte strategia de control inversat este data de:
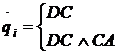 daca N(i) = 0, si N(i)
daca N(i) = 0, si N(i) ![]() 0
0
unde qi - este configuratie lui i si N(i) este numarul de aeronave din zona de protectia a lui i.
Strategia de control este data in figura de mai jos:
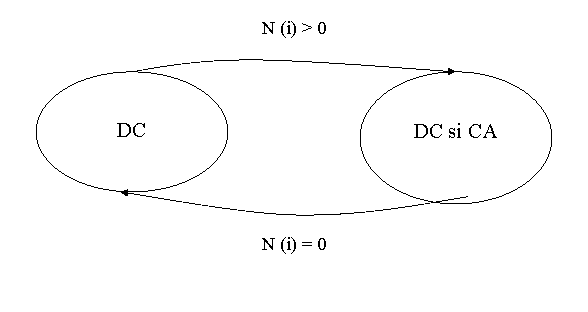
Concluzii :
In aceasta lucrare am demonstrat trei teoreme de stabilitate a sistemelor stohastice inversate . Aceste teoreme sunt extensiile unor rezultate existente din ultimul deceniu . Teoremele dovedite in aceasta lucrare furnizeaza conditii suficiente pentru stabilitatea sistemelor stohastice hibride.
Bibliografie
[1] M.S. Branicky,"Multiple Lyapunov Functions and Other Analysis Tools
for Switched and Hybrid Systems', IEEE Transactions on Automatic
Control,vol.43,No.4,pp.475-482, 1998.
[2] G. Chen, G. Chen and S.H. Hsu,"Linear Stochastic Control Systems', CRC Press, 1995.
[3] M.H.A. Davis,"Markov Models and Optimization',Chapman & Hall 1993.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |