Fluxul campului magnetic
Aplicand operatorul divergenta relatiei (7.5) se obtine:
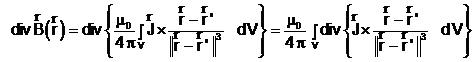
In analiza matematica se demonstreaza urmatoarele relatii:
![]()
In consecinta
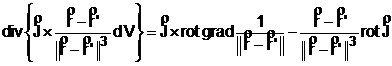
si cum rot ![]() =0 deoarece
=0 deoarece ![]() nu depinde de
nu depinde de ![]() , se obtine
, se obtine
![]() (7.27)
(7.27)
relatie ce constituie forma locala a legii de conservare a fluxului magnetic.
Evaluand
fluxul lui ![]() printr-o
suprafata inchisa S ce delimiteaza un volum V se
obtine:
printr-o
suprafata inchisa S ce delimiteaza un volum V se
obtine:
![]() (7.28)
(7.28)
Relatia (7.28) exprima o
proprietate fundamentala a campului magnetic: fluxul campului magnetic ![]() prin orice
suprafata inchisa este nul.
prin orice
suprafata inchisa este nul.
Se va utiliza aceasta proprietate fundamentala a campului magnetic pentru doua suprafete S1 si S2 care se sprijina pe acelasi contur C (Fig. 7.8).
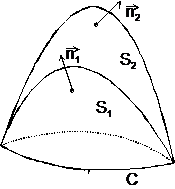
Figura 7.8
Calculand
fluxul vectorului ![]() prin cele doua
suprafete, se obtine:
prin cele doua
suprafete, se obtine:
![]()
Calculand
acum fluxul prin suprafata ![]() se obtine:
se obtine:
![]() (7.29)
(7.29)
Astfel, fluxul nu depinde de suprafata care se sprijina pe conturul considerat, ci numai de acest contur. Se spune ca pentru campul magnetic fluxul este conservativ.
In
analiza matematica se demonstreaza ca pentru orice camp
vectorial div rot![]() =0. Tinand cont de relatia (7.27) se poate afirma
ca exista un camp de vectori
=0. Tinand cont de relatia (7.27) se poate afirma
ca exista un camp de vectori ![]() pentru care:
pentru care:
![]() (7.30)
(7.30)
Acest camp poarta numele de potentialul vector al campului magnetic.
Potentialul
vector astfel introdus nu este complet determinat. Intr-adevar, rotorul
unui gradient fiind nul, relatia (7.30) nu determina vectorul ![]() decat pana la
gradientul unei functii f diferentiabila. Folosind
transformarea:
decat pana la
gradientul unei functii f diferentiabila. Folosind
transformarea:
![]() (7.31)
(7.31)
vectorul ![]() nu va depinde de
alegerea lui f. Transformarea (7.31) poarta numele de transformare de scara.
nu va depinde de
alegerea lui f. Transformarea (7.31) poarta numele de transformare de scara.
Din
relatia (7.31) rezulta ca ![]() nu este o marime
fizica masurabila. In general in magnetostatica se
introduce o conditie suplimentara pentru
nu este o marime
fizica masurabila. In general in magnetostatica se
introduce o conditie suplimentara pentru ![]() :
:
![]() (7.32)
(7.32)
numita conditia lui Coulomb.
Utilizand
forma locala a teoremei Ampère ![]() si relatia
(7.30) se poate scrie:
si relatia
(7.30) se poate scrie:
![]()
Folosind conditia de joja Coulomb, ![]() , se obtine:
, se obtine:
![]() (7.33)
(7.33)
Relatia (7.32) este analoaga ecuatiei Poisson din electrostatica.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |