
Regimul stabil de lucru al motoarelor de curent continuu - Caracteristicile de functionare
Caracteristicile de lucru stabilesc
proprietatile motoarelor in regim stabil de lucru. Aceste caracteristici
reprezinta dependentele: turatiei n, momentului M,
ran-damentului motorului ![]() , de puterea mecanica utila P2 la arborele sau (sau de mari-mea curentului
rotoric Ia) la tensiune
de alimentare constanta, egala cu tensiunea nominala si la
rezistente constante ale circuitelor indusului si de excitatie,
adica
, de puterea mecanica utila P2 la arborele sau (sau de mari-mea curentului
rotoric Ia) la tensiune
de alimentare constanta, egala cu tensiunea nominala si la
rezistente constante ale circuitelor indusului si de excitatie,
adica ![]() sau f(Ia) pentru U=Un=const.
sau f(Ia) pentru U=Un=const.
Dependenta n=f(P2) sau f(Ia) reprezinta caracteristica de viteza a motoarelor de c.c. Obisnuit, in caracteristicile de lucru se include si caracteristica mecanica a motoarelor, care reprezinta dependenta n=f(M).
1 Caracteristicile de lucru ale motoarelor de c.c.
cu excitatie independenta si paralela (motoare sunt)
Diferenta principala intre caracteristicile de lucru ale motoarelor cu excitatie independenta si ale celor cu excitatie paralela nu exista. Alura acestor caracteristici pentru cele doua tipuri de motoare este prezentata in fig.4.35.
![]()
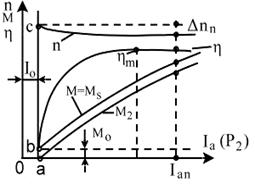
Fig.4.35 Alura caracteristicilor de lucru ale motoarelor de c.c.
cu excitatie independenta si paralela
Caracteristica de viteza n=f(Ia) se poate determina din ecuatia (4.3), ce expri-ma egalitatea t.e.m. si a caderii de tensiune din circuitul indusului:
![]()
De aici se observa ca:
![]() (4.10)
(4.10)
Din expresia (4.10) rezulta, ca la
cresterea curentului Ia
creste caderea de tensiune RaIa din infasurarea
indusului, datorita careia turatia n se reduce. Cu
cresterea insa a curentului Ia
se reduce marimea fluxului magnetic ![]() datorita
reac-tiei indusului si turatia creste. Prin urmare
variatia fluxului magnetic si a caderii de tensiune din
infasurarea indusului sunt doua consecinte ale motivului
variatiei curentului rotoric ce actioneaza invers asupra
modificarii turatiei.
datorita
reac-tiei indusului si turatia creste. Prin urmare
variatia fluxului magnetic si a caderii de tensiune din
infasurarea indusului sunt doua consecinte ale motivului
variatiei curentului rotoric ce actioneaza invers asupra
modificarii turatiei.
Obisnuit, predomina actiunea caderii de tensiune din infasurarea indusului, datorita careia caracteristica de viteza reprezinta aproape o linie dreapta slab incli-nata fata de axa absciselor.
Motoarele cu excitatie independenta si paralela au caracteristica de viteza dura, adica la variatia sarcinii, turatia ramane aproape constanta. Din acest motiv, la cresterea sarcinii, puterea si momentul la aceste motoare cresc aproape propor-tional. Potrivit ecuatiilor (4.4) si (4.6):
![]()
Se observa ca la cresterea
curentului rotoric, momentul M variaza dupa o lege liniara.
Trebuie a se sublinia, ca la cresterea lui Ia, intr-o anumita masura se reduce
si fluxul magnetic ![]() urmare actiunii
reactiei indusului, datorita careia de-pendenta M=f(Ia) nu este pe deplin
liniara. Ea porneste din punctul b, deoarece la functionarea in
gol
urmare actiunii
reactiei indusului, datorita careia de-pendenta M=f(Ia) nu este pe deplin
liniara. Ea porneste din punctul b, deoarece la functionarea in
gol ![]() (fig.4.35).
(fig.4.35).
Avand in vedere ca la ridicarea
caracteristicilor de lucru, turatia si fluxul magnetic raman
aproape constante, se admite ca ![]() Caracteristica
mo-mentului util
Caracteristica
mo-mentului util ![]() se obtine
daca se reduc ordonatele punctelor de pe curba M=f(Ia) cu valoarea momentului M0 la functionarea in gol.
se obtine
daca se reduc ordonatele punctelor de pe curba M=f(Ia) cu valoarea momentului M0 la functionarea in gol.
Randamentul se determina ca raport intre puterea mecanica utila de iesire P2 si puterea electrica P1 de intrare consumata de motor:
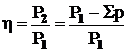 (4.11)
(4.11)
unde: P1=U·Ia, iar ![]() reprezinta suma
diferitelor forme ale pierderilor de putere ce include:
reprezinta suma
diferitelor forme ale pierderilor de putere ce include:
pierderile din infasurarea
de excitatie![]() ;
;
pierderile din infasurarea
indusului![]() ;
;
pierderile mecanice pmec (de frecare in lagare, ventilatie, s.a.);
pierderile in fierul magnetic (pierderi magnetice) pFe;
pierderile suplimentare psupl datorate deformatiei fluxului magnetic la suprasarcina, aparitiei curentilor turbionari in elementele de fixare sau in conductoarele indusului daca ele sunt de sectiune mare s.a.
In conditiile de
examinare n≈const., Φ≈const. si Ia≈const. se poate admite ca pierderile in
fier, in infasurarea de excitatie si pierderile mecanice
sunt constante, adica pFe+pex+pmec=const. Pierderile din infasurarea
indusului pJ si
pierderile supli-mentare ps
sunt variabile, deoarece depind de sarcina motorului (depind de ![]() ).
).
In fig.4.35 este
prezentata dependenta ![]() . Randamentul atinge valoa-rea maxima la acea sarcina, cand
pierderile variabile sunt egale cu cele con-stante. Obisnuit, la
motoarele cu putere mica,
. Randamentul atinge valoa-rea maxima la acea sarcina, cand
pierderile variabile sunt egale cu cele con-stante. Obisnuit, la
motoarele cu putere mica, ![]() , iar cele de putere
, iar cele de putere ![]() . Dupa cum s-a aratat, in grupa caracteristicilor
de lucru se exami-neaza si caracteristica mecanica a motorului
n=f(M). Ea se poate obtine din expre-sia pentru caracteristica vitezei (4.10),
daca se modifica in acord cu ecuatia (4.4):
. Dupa cum s-a aratat, in grupa caracteristicilor
de lucru se exami-neaza si caracteristica mecanica a motorului
n=f(M). Ea se poate obtine din expre-sia pentru caracteristica vitezei (4.10),
daca se modifica in acord cu ecuatia (4.4):
![]() (4.12)
(4.12)
Din expresia (4.12) se observa ca
aceasta caracteristica mecanica are carac-ter
asemanator cu caracteristica vitezei, adica dupa cum s-a
aratat la Ie=const.
se poate admite ca ![]() , la care caracteristicile mecanice ale motoarelor cu
excitatie paralela si independenta sunt linii drepte,
inclinate fata de axa absciselor. Iata de ce in practica,
se considera sau caracteristica de viteza sau caracteristica
mecanica a motoarelor.
, la care caracteristicile mecanice ale motoarelor cu
excitatie paralela si independenta sunt linii drepte,
inclinate fata de axa absciselor. Iata de ce in practica,
se considera sau caracteristica de viteza sau caracteristica
mecanica a motoarelor.
Segmentul determinat de caracteristica
mecanica pe axa ordonatelor ![]() reprezinta
turatia motorului la functionarea in gol ideal, iar coeficientul
negativ
reprezinta
turatia motorului la functionarea in gol ideal, iar coeficientul
negativ 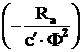 stabileste
unghiul de inclinare al caracteristicii fata de axa absciselor.
stabileste
unghiul de inclinare al caracteristicii fata de axa absciselor.
Atunci cand motorul functioneaza in
conditii: U=Un, ![]() si in lipsa
rezistentelor suplimentare din circuitul indusului se poate considera
asa numita caracteristica mecanica naturala (c.m.n.) a
motorului. In toate celelalte cazuri se obtin caracteristici mecanice
artificiale. Asemenea se considera si pentru
caracte-risticile de viteza. In fig.4.36 sunt indicate caracteristicile
mecanice (de viteza) ale motoarelor de excitatie paralela
si independenta.
si in lipsa
rezistentelor suplimentare din circuitul indusului se poate considera
asa numita caracteristica mecanica naturala (c.m.n.) a
motorului. In toate celelalte cazuri se obtin caracteristici mecanice
artificiale. Asemenea se considera si pentru
caracte-risticile de viteza. In fig.4.36 sunt indicate caracteristicile
mecanice (de viteza) ale motoarelor de excitatie paralela
si independenta.
Caracteristica mecanica naturala
(c..m.n.)
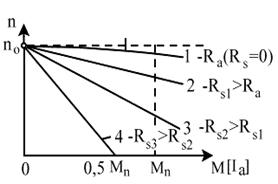
Fig.4.36 Caracteristicile mecanice (de viteza) ale motoarelor de c.c.
1 - caracteristica mecanica naturala; 2, 3, 4, caracteristici mecanice artificiale
obtinute pentru diferite rezistente suplimentare in circuitul rotoric (RS3>RS2>RS1>Ra)
Dreapta 1 reprezinta caracteristica mecanica naturala (c.m.n.), iar dreptele 2, 3 si 4 sunt caracteristicile mecanice artificiale, obtinute la conectarea de rezistente suplimentare Rs (fig.4.33 a,b) in circuitul indusului. La conectarea de rezistente suplimentare Rs in circuitul indusului, caracteristica mecanica se deter-mina cu expresia:
![]() (4.13)
(4.13)
Din expresia (4.13) se vede, ca cu cat
valoarea pentru Rs este
mai mare, cu atat caracteristica artificiala este mai inclinata (mai
cazatoare) fata de axa absci-selor. Avand in vedere ca
![]() si
si ![]() toate caracteristicile
determina seg-mente egale pe axa ordonatelor, adica ele se
intersecteaza in acelasi punct determi-nat de turatia n0 corespunzatoare
functionarii in gol ideal.
toate caracteristicile
determina seg-mente egale pe axa ordonatelor, adica ele se
intersecteaza in acelasi punct determi-nat de turatia n0 corespunzatoare
functionarii in gol ideal.
In fig.4.37 sunt prezentate caracteristicile
mecanice naturala si artificiale, obtinute la diferite tensiuni
de alimentare U pentru ![]() , Rs=0.
, Rs=0.
Din expresiile (4.12) si (4.13) se observa ca, cu cat tensiunea este mai mica in raport cu cea nominala, cu cat segmentele determinate de caracteristicile meca-nice artificiale pe axa ordonatelor sunt mai mici. Caracteristicile separate sunt paralele una fata de alta, deoarece variatia tensiunii de alimentare nu influenteaza asupra inclinarii caracteristicilor fata de axa absciselor (ecuatiile 4.12 si 4.13).
In fig.4.38 se prezinta caracteristicile
mecanice pentru motoarele de c.c. cu excitatie independenta si
paralela, ridicate pentru marimi diferite ale fluxului ![]() si la U=Un si Rs=0.
si la U=Un si Rs=0.
Variatia fluxului magnetic
influenteaza atat marimea segmentelor deter-minate pe axa de
ordonate ale caracteristicilor, cat si asupra inclinarii lor
fata de axa absciselor. Cu
reducerea fluxului ![]() , segmentele si inclinarile cresc si invers.
, segmentele si inclinarile cresc si invers.
In conditii naturale de functionare, motoarele de c.c. cu excitatie paralela si independenta au caracteristici mecanice (de viteza) dure.
Caracteristica mecanica naturala (c.m.n). Caracteristica mecanica naturala (c.m.n).
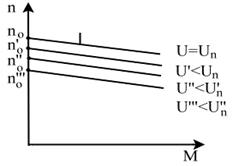
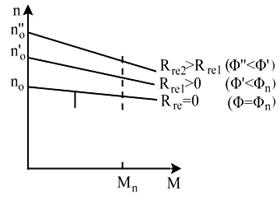
Fig.4.37 Caracteristicile mecanice naturala Fig.4.38 Caracteristicile, mecanice pentru
si artificiale, obtinute la diferite tensiuni de motoarele de c.c. cu excitatie independenta
alimentare U pentru ![]() , Rs=0 si paralela,
ridicate pentru marimi diferite
, Rs=0 si paralela,
ridicate pentru marimi diferite
ale
fluxului ![]() la U=Un si Rs=0
la U=Un si Rs=0
Datorita caracterului cazator al caracteristicilor mecanice (de viteza), motoa-rele cu excitatie paralela si independenta functioneaza stabil. In fig.4.39 sunt indicate caracteristica mecanica n=f(M) si caracteristica momentului rezistent Mr=const.
In regimul stabil de functionare, cand
M=Mr (punctul A de
intersectie al caracteristicilor), motorul functioneaza la turatia
n stabilita. Daca dintr-un anumit motiv, turatia n se reduce la ![]() , momentul motorului M creste pana la
, momentul motorului M creste pana la ![]() si devine mai
mare decat momentul rezistent Mr.
Atunci, potrivit ecuatiei de echilibru a momentelor la arborele motorului
se exercita momentul dinamic pozitiv. Acesta determina cresterea
turatiei si corespunzator se reduce momentul motorului la M=Mr, cand masina din nou
incepe sa functioneze stabil in punctul A cu turatia n.
si devine mai
mare decat momentul rezistent Mr.
Atunci, potrivit ecuatiei de echilibru a momentelor la arborele motorului
se exercita momentul dinamic pozitiv. Acesta determina cresterea
turatiei si corespunzator se reduce momentul motorului la M=Mr, cand masina din nou
incepe sa functioneze stabil in punctul A cu turatia n.
Daca din orice motiv turatia
creste de la n la ![]() , momentul M al motorului se reduce la
, momentul M al motorului se reduce la ![]() si devine mai mic
decat momentul rezistent Mr.
Asupra arborelui masinii se exercita momentul dinamic negativ,
datorita caruia turatia se reduce de la
si devine mai mic
decat momentul rezistent Mr.
Asupra arborelui masinii se exercita momentul dinamic negativ,
datorita caruia turatia se reduce de la ![]() la n si motorul
din nou incepe sa functioneze stabil in punctul A, unde momentele
motor si rezistent (de sarcina) se echilibreaza reciproc.
la n si motorul
din nou incepe sa functioneze stabil in punctul A, unde momentele
motor si rezistent (de sarcina) se echilibreaza reciproc.
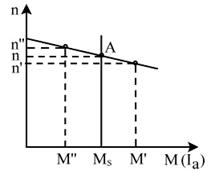
Fig.4.39 Caracteristicile mecanica n=f(M)si a momentului rezistent Mr=const.
pentru motoarele de c.c. cu excitatie paralela si independenta
Atunci cand motoarele de c.c. cu excitatie independenta sau paralela func-tioneaza in regim stabil si se obtine intreruperea circuitului infasurarii de excitatie, fluxul magnetic devine foarte mic (tinde spre fluxul de magnetizare remanenta). In acest caz, potrivit ecuatiei (4.10), turatia creste rapid si obtine valori, periculoase cu consecintele sale - ruperea bandajelor, defectarea infasurarii indusului s.a. Iata de ce la intreruperea circuitului de excitatie, motorul trebuie decuplat fara intar-ziere de la reteaua de alimentare.
In practica au aplicare larga motoarele cu excitatie derivatie, si motoarele cu excitatie independenta (ultimele in sistemele de generator-motor).
2. Caracteristicile de lucru ale motoarelor
cu excitatie serie (motoare serie)
La motoarele cu excitatie serie,
deoarece Ie=Ia si pentru sistemul
magnetic nesaturat al masinii ![]() , si daca se substituie in ecuatia (4.10)
, si daca se substituie in ecuatia (4.10) ![]() , se obtine expresia caracteristicii de viteza
pentru aceste motoare:
, se obtine expresia caracteristicii de viteza
pentru aceste motoare:
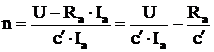 (4.14)
(4.14)
unde:
Ra - suma rezistentelor infasurarii indusului si infasurarii de excitatie serie.
Din expresia (4.14) rezulta, ca aceasta caracteristica de viteza a motoarelor de c.c. cu excitatie serie reprezinta o hiperbola patrata ale carei asimptote coincid cu axele de coordonate (fig.4.40).
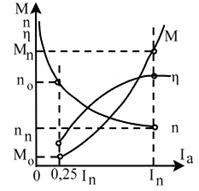
Fig.4.40. Caracteristica de viteza a motorului de c.c. cu excitatie serie
La cresterea curentului, masina se
satureaza si turatia se modifica mai putin.
Caracteristica de viteza a motoarelor cu excitatie serie are un
puternic caracter cazator. Asemenea caracteristica este
numita moale. La regimul de functionare in gol Ie=Ia=0 si de aici si ![]() , datorita caruia, turatia creste rapid
si atinge valori periculoase sub aspect mecanic pentru
motor(determina ruperea bandajelor, defec-tarea infasurarii
indusului s.a.).
, datorita caruia, turatia creste rapid
si atinge valori periculoase sub aspect mecanic pentru
motor(determina ruperea bandajelor, defec-tarea infasurarii
indusului s.a.).
De aceea, motoarele serie trebuie sa
functioneze in conditii ce exclud posi-bilitatea obtinerii
regimului de functionare in gol. In acest scop, legatura
dintre motor si masina de lucru se realizeaza prin transmisie
dintata si in unele cazuri prin transmisie cu curea, deoarece in
procesul de functionare, cureaua se poate rupe si masina trece
in regimul de functionare in gol, periculos pentru ea. Obisnuit,
mo-toarele serie se dimensioneaza astfel, incat sa suporte
fara consecinte periculoase pana la 50% peste turatia
lor nominala de rotatie. Pornirea si functionarea acestor
motoare la sarcina sub 25% din cea nominala este inadmisibila.
Dupa cum anterior s-a subliniat, pentru sistemul magnetic nesaturat al
masinii, fluxul magnetic este proportional cu marimea curentului
rotoric (![]() ). In acest caz pentru momentul motorului se obtine:
). In acest caz pentru momentul motorului se obtine:
![]() (4.15)
(4.15)
Din expresia (4.15) se observa, ca
la cresterea sarcinii, momentul motorului cu excitatie serie
variaza dupa o lege parabolica (fig.4.40).
Cresterea mai rapida a
momentului motor la motoarele serie in comparatie cu motoarele cu
excitatie paralela, la care ![]() le face potrivite in
regimurile grele de functio-nare - conditii grele de pornire,
combinate cu suprasarcini importante la arbore cu viteze mici, cum se
intalneste de exemplu in tractiunea electrica, la
instalatiile miniere de ridicat s.a.
le face potrivite in
regimurile grele de functio-nare - conditii grele de pornire,
combinate cu suprasarcini importante la arbore cu viteze mici, cum se
intalneste de exemplu in tractiunea electrica, la
instalatiile miniere de ridicat s.a.
La motoarele serie insa exista
proprietatea, ca la variatia sarcinii se modifica toate formele
de pierderi din masina. Datorita faptului, ca Ie=Ia, pierderile din infa-surarea de
excitatie sunt variabile si se considera impreuna cu cele
din infasurarea indusului, adica ![]() (Ra - suma rezistentelor
infasurarilor indusului
si de excitatie).
(Ra - suma rezistentelor
infasurarilor indusului
si de excitatie).
Pe langa aceasta, la cresterea sarcinii,
turatia n se reduce si deci se reduc si pierderile mecanice pmec si in acelasi
timp se amplifica inductia magnetica, datorita careia
pierderile in circuitul magnetic cresc. Se dovedeste ca, reducerea pmec are loc atat cat este
cresterea pFe,
datorita careia suma lor este o marime aproximativ
cons-tanta. Iata de ce si la motoarele cu excitatie serie
se poate vorbi de pierderi cons-tante si variabile, unde prin pierderi
constante se intelege suma pierderilor meca-nice si celor din fierul
magnetic, adica ![]() Si aici, valoarea
maxima a randamentului η se obtine la acea sarcina a
masinii pentru care pierderile variabile sunt egale cu cele constante.
Dependenta
Si aici, valoarea
maxima a randamentului η se obtine la acea sarcina a
masinii pentru care pierderile variabile sunt egale cu cele constante.
Dependenta ![]() este prezentata
in fig.4.40.
este prezentata
in fig.4.40.
Caracteristica mecanica n=f(M) pentru
motoarele cu excitatie serie se obtine, daca in expresia
caracteristicii de viteza (4.14) se substituie ![]()
![]() :
:
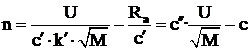 (4.16)
(4.16)
Din expresia (4.16) se observa, ca pentru circuit magnetic nesaturat, caracteristica mecanica a motoarelor serie are forma de hiperbola, adica ea este asemanatoare caracteristicii de viteza.
![]()
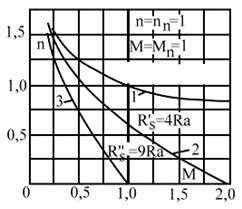
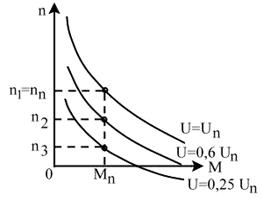
Fig.4.41. Caracteristicile mecanica Fig.4.42 Caracteristile mecanice
naturala (1) si artificiale rezistive naturala si artificiale de tensiune
(2,3) ale motorului de c.c. serie ale motorului de c.c. serie
In fig.4.41 sunt prezentate:
caracteristica mecanica naturala 1 ridicata pentru Rs=0;
caracteristicile mecanice artificiale
2 si 3 ridicate corespunzator la introducerea de rezistente
suplimentare ![]() si
si ![]() (
(![]() ) in cir-cuitul indusului (fig.4.33 c).
) in cir-cuitul indusului (fig.4.33 c).
In fig.4.42 sunt prezentate caracteristica mecanica naturala si doua caracteris-tici mecanice artificiale ridicate la diferite tensiuni si Rs=0. Intrucat caracteristi-cile mecanice (de viteza) ale motoarelor serie au caracter cazator, aceste motoare functioneaza totdeauna stabil.
3 Caracteristicile de lucru ale motoarelor
cu excitatie mixta (motoare compundate)
La motoarele cu excitatie mixta, infasurarile de excitatie serie si paralel pot fi conectate in acelasi sens sau in sens invers. Conectarea in sens invers se utilizeaza foarte rar, deoarece in acest caz, cele doua infasurari de excitatie creaza fluxuri opuse, iar proprietatile la pornire ale motoarelor se inrautatesc. Pe langa aceasta, aceste motoare functioneaza instabil, deoarece datorita actiunii demagnetizante a infasurarii de excitatie serie cu cresterea sarcinii, turatia creste nelimitat.
Alura caracteristicii motoarelor cu conectare in acelasi sens a infasurarilor de excitatie depinde de raportul t.m.m. create de cele doua infasurari. Daca predomi-na actiunea infasurarii in paralel, caracteristicile motoarelor sunt apropiate de cele ale motoarelor sunt, iar daca predomina infasurarea serie, caracteristicile se apropie de cele ale motorului serie.
Expresia pentru caracteristica de viteza a motoarelor cu excitatie mixta este:
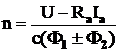 (4.17)
(4.17)
unde:
Ra - suma rezistentelor infasurarilor indusului si de excitatie in parale
si in serie;
![]() - fluxurile magnetice create de infasurarile
de excitatie paralela si
- fluxurile magnetice create de infasurarile
de excitatie paralela si
serie;
Semnele "+" si "-" se atribuie corespunzator cand fluxurile magnetice ale celor doua infasurari au acelasi sens sau sens invers. Momentul motor se deter-mina cu expresia:
![]() (4.18)
(4.18)
Din ecuatiile (4.17) si (4.18) usor se obtine expresia caracteristicii meca-nice:
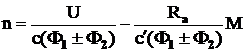 (4.19)
(4.19)
Randamentul se determina analog celor pana acum studiate la motoarele de c.c. In fig.4.43 a se prezinta caracteristica de viteza 1 a motorului cu excitatie mixta. In aceeasi figura, cu 2 si 3 sunt notate caracteristicile motoarelor sunt si serie. In fig.4.43 b se prezinta dependenta M=f(Ia) a motorului compundat - curba 1, iar curbele 2 si 3 reprezinta aceleasi dependente, corespunzatoare motorului cu excitatie in paralel si serie. In fig.4.43 c sunt indicate caracteristicile mecanice ale motoarelor compundat, sunt si serie, corespunzator prin curbele 1, 2 si 3.
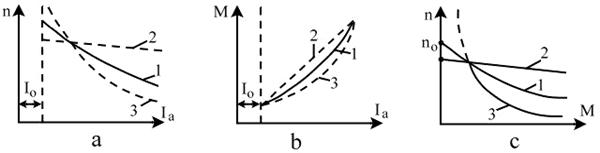
Fig.4.43 a) caracteristicile de viteza ale motorului de c.c. cu excitatie mixta - curba 1;
motoarelor de c.c. cu excitatie paralela - curba 2 si mixta - curba 3; b) dependenta M=f(Ia) pentru: motorul compundat curba 1, pentru motorul de c.c. excitat in paralel - curba 2
si pentru motorul de c.c. cu excitatie in serie - curba 3; c) caracteristicile de viteza pentru motoarele de c.c.: compundat - curba 1; sunt - curba 2, cu excitatie in serie - curba 3
Avantajul caracteristic motoarelor cu excitatie mixta fata de motoarele cu excitatie serie este ca pot functiona in regim de gol. De aceea ele se utilizeaza in transportul electric (tramvai, troleibuz, locomotive electrice) deoarece partea de baza a fluxului magnetic este creata de infasurarea de excitatie serie, iar infasurarea paralel serveste numai la evitarea cresterii inadmisibile a turatiei la sarcini mici. Se utilizeaza de asemenea la actionarea masinilor de valtuit, pompelor, compresoa-relor s.a.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |