
1.Studiul elementelor de intarziere de ordinul 1.
1.1. Deducerea analitica a raspunsului indicial prin rezolvarea ecuatiei diferentiale
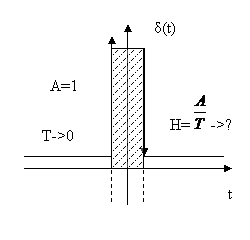 Semnalul impuls unitar (functia delta sau functia Dirac)
Semnalul impuls unitar (functia delta sau functia Dirac)
Este un impuls idealizat de latime foarte mica si de arie unitara.
Masura lui δ(t) => A=1
L[δ(t)] = 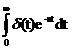 =
= 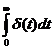 =1
=1
Raspunsul SLN (element), a lui δ(t), in conditii initiale nule se numeste raspuns unitar sau functie pondere [w(t)]
δ(t) = 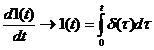
Relatii simetrice:
w(t) = 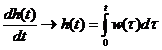
Utilizarea functiei pondere:
Cunoscand pe [w(t)] si utilizand integrala de convolutie reala se determina raspunsul sistemului pentru orice referinta r(t).
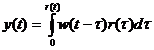 ;
; ![]()
1.2. Deducerea analitica a raspunsului indicial in baza F.D.T si respectiv a functiei pondere(integrala de convolutie reala)
Ecuatia:
T![]() + y(t) = r(t)
+ y(t) = r(t)
T![]() + y = r ; r = 1(t); y(0) = 0
+ y = r ; r = 1(t); y(0) = 0
Functia de transfer:
TsY(s) + 1 = R(s)
G(s) = ![]()
G(s) = ![]()
Din teorema valorii finale:
y![]() =
= ![]() y(t) =
y(t) = ![]() Y(s) =
Y(s) = ![]() [s*R(s)*G(s)] =
[s*R(s)*G(s)] = ![]() [s*
[s*![]() *G(s)] = G(0) = 1
*G(s)] = G(0) = 1
y![]() = 1
= 1
ε![]() = y
= y![]() - r(t) = 1 - 1 = 0;
- r(t) = 1 - 1 = 0;
ε![]() = 0
= 0
Prin rezolvarea directa a ecuatiei diferentiale
 Ecuatia diferentiala:
Ecuatia diferentiala:
T![]() (t)+ y(t) = r(t); r(t) = 1(t), y(0) = 0
(t)+ y(t) = r(t); r(t) = 1(t), y(0) = 0
Ecuatia caracteristica:
![]() => Tp + 1 = 0
=> Tp + 1 = 0
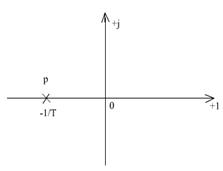 Radacina ecuatiei caracteristica :
Radacina ecuatiei caracteristica :
p = -![]()
Solutia ecuatiei omogene:
y![]() (t) = C*e
(t) = C*e![]() =C*e
=C*e![]() ; t≥0
; t≥0
Valoarea de regim stationar:
y![]() = constant -> y
= constant -> y![]() =1
=1
 Solutia complexa:
Solutia complexa:
y(t) = y![]() (t) + y
(t) + y![]() = 1 + C*e
= 1 + C*e![]() ; t≥0
; t≥0
Calculul C:
y(0) = 1 +C = 0 =>C=-1
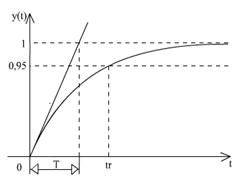
y(t) = h(t) = 1- e![]() ; t≥0
; t≥0
ε![]() = 0
= 0
tr ≈ 3T
![]() y(t) = k(1 - e
y(t) = k(1 - e![]() ); t≥0
); t≥0
1.3. Intocmirea schemelor de modelare in Simulink.
1.3.1. Schema de modelare in baza ecuatiei diferentiale.
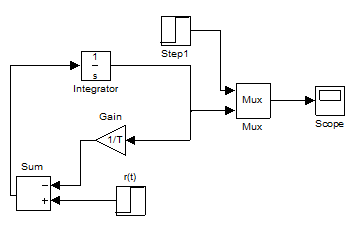
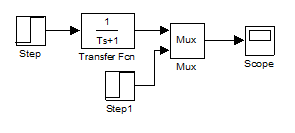
1.3.2. Schema de modelare in baza functiei de transfer.
![]()
1.4. Calculul raspunsului indicial si a functiei pondere in Matlab
%secvente Matlab
t=0:0.1:30
num=[1]
den=[5 1]
ys=step(num,den,t);
v=t;
df1=diff(v)./diff(t);
df2=0.95*df1;
td=t(2:length(t));
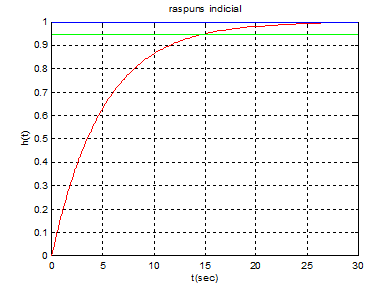
plot(t,ys,'-r',td,df1,'-b',td,df2,'-g');grid
title('raspuns indicial')
xlabel('t(sec)')
ylabel('h(t)')
gtext('g(s)=1/(5s+1)');
[x,y]=ginput
%Calculul functiei pondere
%ptr el aperiodic de ord 1 cu f.d.t.
%G(s)=1/(5s+1)
t=0:0.1:30
num=[1]
den=[5 1]
yi=impulse(num,den,t);
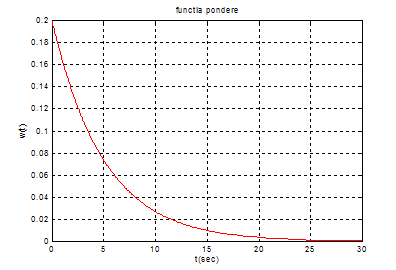
plot(t,yi,'-r');grid
title('functia pondere')
xlabel('t(sec)')
ylabel('w(t)')
gtext('G(s)=1/(5s+1)');
[x,y]=ginput
1.5. Determinarea performantelor in raport cu referinta treapta unitara pentru K=1 si T=1.5(s), utilizand una din variantele 1.3.1., 1.3.2. sau 1.4.
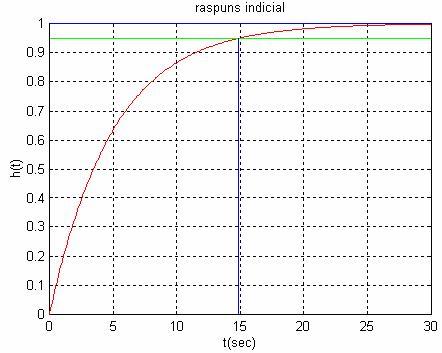
Performante de regim stationar:
![]() (valoare de regim
stationar)
(valoare de regim
stationar)
![]() (eroare stationara,
sistem astatic)
(eroare stationara,
sistem astatic)
Performante de regim tranzitoriu:
![]() (timp de raspuns, timp
de reglare)
(timp de raspuns, timp
de reglare)
![]() (suprareglaj)
(suprareglaj)
![]() (grad de amortizare)
(grad de amortizare)
1.6. Calculul caracteristicilor de frecventa U(ω), V(ω), A(ω), φ(ω), U(ω)/V(ω) pentru K=1 si T=1.5(s)
Ecuatia:
1.5![]() +y(t)=r(t), unde r(t)=1(t)
+y(t)=r(t), unde r(t)=1(t)
1.5![]() +1=r
+1=r
Aplicam transformata directa Laplace in conditii initiale nule:
1.5sY(s)+Y(s)=R(s)
Deducem functia de transfer:
1.5sY(s)+Y(s)=R(s)
![]()
1.5s![]() +
+![]() =1
=1
![]() (1.5s+1)=1
(1.5s+1)=1
G(s)=![]()
![]() Facem schimbarea de variabila s=jω:
Facem schimbarea de variabila s=jω:
W(jω)=![]() =
=![]() =
=![]() =
=![]() -
- ![]() j U(ω)=
j U(ω)= ![]()
W(jω)=A(ω)e![]() =U(ω)+jV(ω) V(ω)=-
=U(ω)+jV(ω) V(ω)=- ![]()
A(ω)=![]() =
=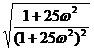 =
=![]()
φ(ω)=arctg![]() =arctg(-5ω)=-arctg(5ω)
=arctg(-5ω)=-arctg(5ω)
1.7. Calculul caracteristicilor logaritmice de frecventa A(ω)[db] si φ(ω)[db], cu program in MATLAB (K=10, T=5(s))
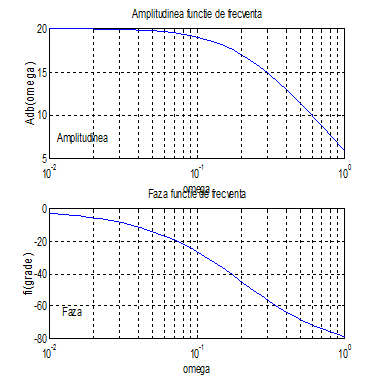 » %Calculul caracteristicilor logaritmice
» %Calculul caracteristicilor logaritmice
» %G(s)=10/(5s+1)
» %Secvente matlab
» w=logspace(-100,10,100)
» num=[10]
» den=[5 1]
» [mag,phase,w]=bode(tf(num,den));
» subplot(211)
» semilogx(w,20*log10(mag)); grid
» xlabel('omega')
» ylabel('Adb(omega)')
» title('Amplitudinea functie de frecventa')
» gtext('Amplitudinea')
» subplot(212)
» semilogx(w,phase); grid
» xlabel('omega')
» ylabel('fi(grade)')
» title('Faza functie de frecventa')
» gtext('Faza')
2. Studiul sistemului liniar neted invariant de ordin 2.
2.1. Deducerea analitica a raspunsului indicial si a performantelor pentru ξ=0, 0<ξ<1, ξ=1, ξ>1
Ecuatia diferentiala:
a![]()
![]() +a
+a![]()
![]() +a
+a![]() y=b
y=b![]() r; r(t)=1(t); y(0)=
r; r(t)=1(t); y(0)=![]() (0)=0
(0)=0
Coeficientii a![]() , i=
, i=![]() depind de parametrii sistemului. Intereseaza influenta
parametrilor asupra raspunsului.
depind de parametrii sistemului. Intereseaza influenta
parametrilor asupra raspunsului.
Pentru a simplifica analiza se introduc 2 coeficienti:
factorul de amortizare: ξ
pulsatia naturala a sistemului
neamortizat: ω![]()
Se aduce ecuatia diferentiala la forma:
![]()
![]()
![]() +2 ξ ω
+2 ξ ω![]()
![]() + ω
+ ω![]()
![]() y=k ω
y=k ω![]()
![]() r
r
![]() +
+![]()
![]() +
+![]() y=
y=![]() r
r
![]() ω
ω![]()
![]() =
=![]() ; ω
; ω![]() =
=![]()
![]()
![]() =
=![]() *
*![]() =k ω
=k ω![]()
![]() ; k=
; k=![]() - coeficientul de amplificare a sistemului
- coeficientul de amplificare a sistemului
2 ξ ω![]() =
=![]() ; ξ=
; ξ=![]() =
=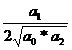 ; ξ≥0
; ξ≥0
Valoarea de regim stationar:
y![]() = constant -> y
= constant -> y![]() =k=constant
=k=constant
Eroarea stationara:
ε![]() =1- y
=1- y![]() =1-k≠0; ε
=1-k≠0; ε![]() =0; k=1
=0; k=1
![]() +2 ξ ω
+2 ξ ω![]()
![]() + ω
+ ω![]()
![]() y=k ω
y=k ω![]()
![]() r ;
r ;
y(t)=y![]() (t)+ y
(t)+ y![]() ; in care y
; in care y![]() =1
=1
y![]() (t)=?
(t)=?
Ecuatia diferentiala omogena:
![]() +2 ξ ω
+2 ξ ω![]()
![]() + ω
+ ω![]()
![]() y
y![]() =0;
=0;
Ecuatia caracteristica:
![]() ;
;
p![]() +2 ξ ω
+2 ξ ω![]() p+ ω
p+ ω![]()
![]() =0;
=0;
Radacinile ecuatiei caracteristice:
p![]() = - ξ ω
= - ξ ω![]() ±j ω
±j ω![]()
![]() ; j=
; j=![]()
p![]() = - ξ ω
= - ξ ω![]() + j ω
+ j ω![]()
![]() ;
;
p![]() = - ξ ω
= - ξ ω![]() - j ω
- j ω![]()
![]() ;
;
Solutia ecuatiei omogene:
y![]() (t)=C
(t)=C![]() e
e![]() +C
+C![]() e
e![]()
Raspunsul:
y(t)
= y![]() + y
+ y![]() (t)=1+ C
(t)=1+ C![]() e
e![]() +C
+C![]() e
e![]() ; t≥0;
; t≥0;
C![]() =?; C
=?; C![]() =? => din conditiile initiale.
=? => din conditiile initiale.
![]()
![]() y(0)=1+ C
y(0)=1+ C![]() +C
+C![]() =0 C
=0 C![]() =
=![]() ;
;
y(0)=
p![]() C
C![]() + p
+ p![]() C
C![]() =0 C
=0 C![]() =
=![]()
y(t)=1-![]() e
e![]() +
+![]() e
e![]() ; t≥0;
; t≥0;
Raspunsul
y(t) depinde de p![]() , p
, p![]() care depinde de coeficientul ecuatiei diferentiale ξ,
ω
care depinde de coeficientul ecuatiei diferentiale ξ,
ω![]() , care depinde de valorile a
, care depinde de valorile a![]() , i=
, i=![]() .
.
a.
ξ=0 - raspunsul este la
limita de stabilitate: p![]() = ±j ω
= ±j ω![]()
y(t)=
1-cos ω![]() t
t
T![]() =1(s);
=1(s);
ω![]() =2πf
=2πf![]() =
=![]() =2π;
=2π;
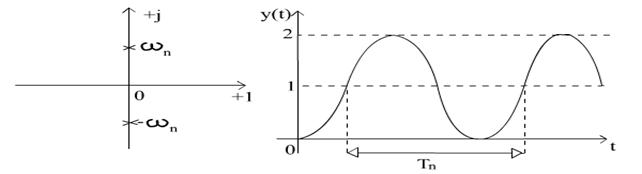
Pentru ξ=0 axa imaginilor in planul radacinilor este axa limitei de stabilitate.
b.
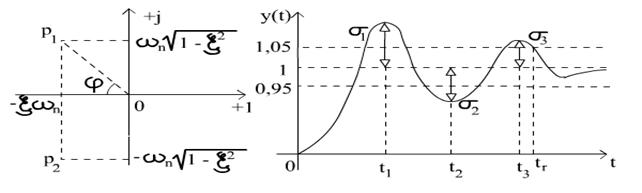
0< ξ<1 - raspuns
oscilant: p![]() = - ξ ω
= - ξ ω![]() ±j ω
±j ω![]()
![]() - pereche de radacini complexe conjugate cu axa reala
negativa.
- pereche de radacini complexe conjugate cu axa reala
negativa.
φ - variabila suplimentara care simplifica scrierea solutiei.
sinφ=![]() ; cos φ= ξ
; cos φ= ξ
tgφ=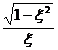
y(t)=
y![]() +y
+y![]() (t)=1-
(t)=1-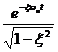 sin(ω
sin(ω![]()
![]() t+arctg
t+arctg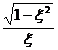 ); t≥0;
); t≥0;
Eroarea stationarii:
ε![]() = 0
= 0
Suprareglajul:
σ=y![]() -y
-y![]() = y
= y![]() -1;
-1;
![]() y
y![]() =?
=?
![]() =0 -> t
=0 -> t![]() =k
=k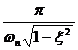 k=0 -> t
k=0 -> t![]() =0 -> y(0)=0
=0 -> y(0)=0
k=1 -> t![]() =
=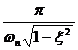
y(t![]() )=1+e
)=1+e![]() =1+σ; σ=e
=1+σ; σ=e![]() ; σ=f(ξ);
; σ=f(ξ);
Gradul de amortizare:
ψ=1-![]() =1-
=1-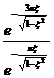 =1-e
=1-e![]()
Timp de raspuns:
t![]() ≈
≈![]()
c.
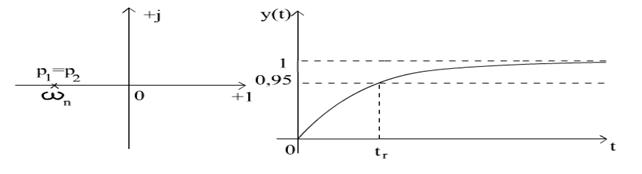
ξ=1 - raspuns aperiodic
critic: p![]() =p
=p![]() =-ω
=-ω![]() (radacini multiple reale negative)
(radacini multiple reale negative)
y(t)=1-(1+ω![]() )e
)e![]() , t≥0
, t≥0
d. ξ>1 - raspunsul supraarmotizat: radacini reale negative simple
e.
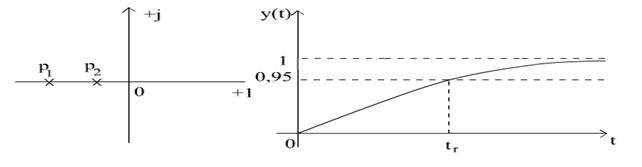
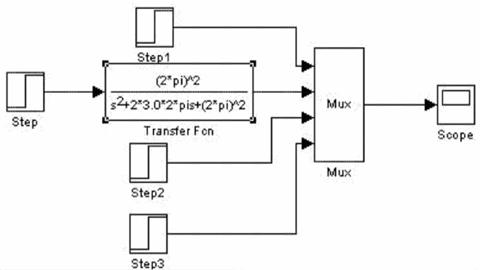
2.2. Intocmirea schemelor de modelare in SIMULINK
2.2.1. Schema de modelare in baza ecuatiei diferentiale
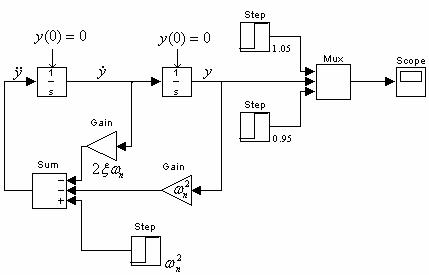
![]()
![]()
2.2.2 Schema de modelare in baza functiei de transfer
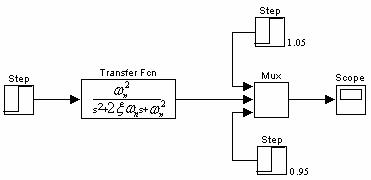
![]()
2.2.3. Schema de modelare in baza varabilelor de stare
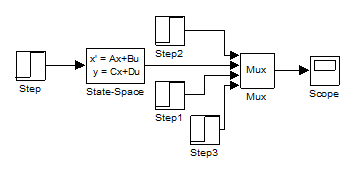
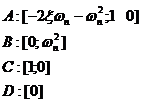
2.3. Calculul functiei
pondere, cu program in MATLAB pentru ξ=0,5 si ω![]() =2π
=2π
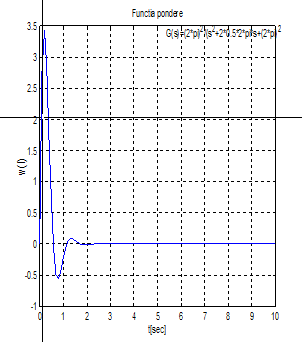 Ecuatia:
Ecuatia:
![]() +2 ξ ω
+2 ξ ω![]()
![]() + ω
+ ω![]()
![]() y=k ω
y=k ω![]()
![]() r, k=1, r=1(t),
r, k=1, r=1(t), ![]() (0)=y(0)=0
(0)=y(0)=0
» %Functia pondere
» %G(S)=(2*pi)^2/(s^2+2*0,5*2*pi+(2*pi)^2)
» %Secvente Mathlab
» t=0:0.1:10
» num=[(2*pi)^2]
» den=[1 2*0.5*2*pi (2*pi)^2]
» yi=impulse(num,den,t)
» plot(t,yi,'-b'); grid
» title('Functia pondere')
» xlabel('t[sec]')
» ylabel('w(t)')
» gtext('G(s)=(2*pi)^2/(s^2+2*0.5*2*pi*s+(2*pi)^2')
» [x,y]=ginput
2.4. Calculul raspunsului indicial, cu program in MATLABpentru
ξ=0,5 si ω![]() =2π
=2π
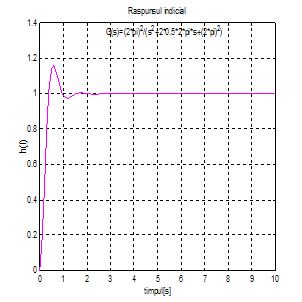 » %Calculul raspunsului indicial
» %Calculul raspunsului indicial
» %G(s)=(2*pi)^2/(s^2+2*0.5*2*pi*s+(2*pi)^2)
» %Secvente Matlab
» t=0:0.1:10
» num=[(2*pi)^2]
» den=[1 2*0.5*2*pi (2*pi)^2]
» ys=step(num,den,t);
» yst=1;
» y=t;
» df1=diff(y)/diff(t);
» df2=0.95*df1;
» df3=1.05*df1;
» td=t(2:length(t));
» plot(t,ys,'-m',td,df1,'-b',td,df2,'-g',td,df3,'-y'); grid
» xlabel('timpul[s]')
» ylabel('h(t)')
» title('Raspunsul indicial')
» gtext('G(s)=(2*pi)^2/(s^2+2*0.5*2*pi*s+(2*pi)^2)')
» [x,y]=ginput
2.5. Determinarea performantelor in raport cu referinta treapta unitara
pentru T![]() =1(s); ωn =2π/Tn=2 π; ξ=0,25; 0,707;1; 3; utilizand una din variantele
2.2.1.,2.2.2., 2.2.4. .
=1(s); ωn =2π/Tn=2 π; ξ=0,25; 0,707;1; 3; utilizand una din variantele
2.2.1.,2.2.2., 2.2.4. .
a) Pentru ξ=0,25 (oscilant amortizat):
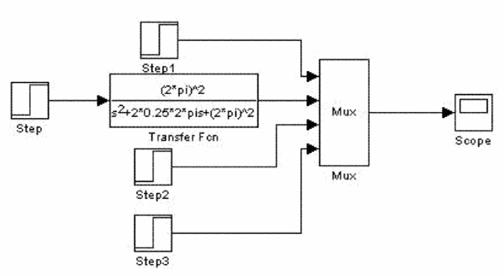
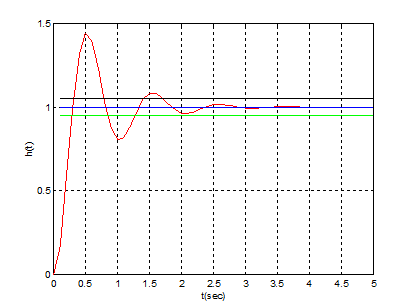 :
:
Performante de regim stationar:
![]() (valoare de regim
stationar)
(valoare de regim
stationar)
![]() (eroare stationara,
sistem astatic)
(eroare stationara,
sistem astatic)
Performante de regim tranzitoriu:
![]() (timp de raspuns, timp
de reglare)
(timp de raspuns, timp
de reglare)
![]() (suprareglaj)
(suprareglaj)
![]() (grad de amortizare)
(grad de amortizare)
b) Pentru ξ=0,707 (oscilant amortizat):
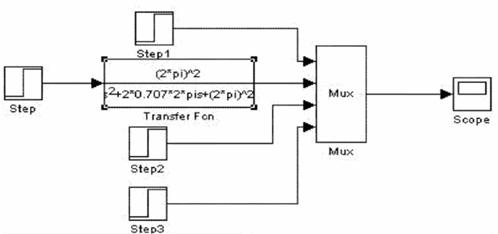
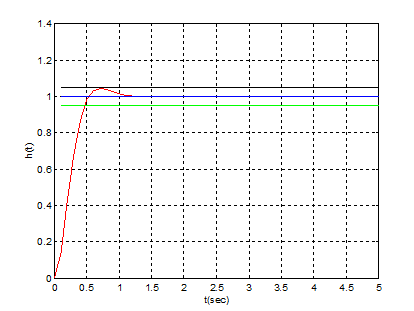
Performante de regim stationar:
![]() (valoare de regim
stationar)
(valoare de regim
stationar)
![]() (eroare stationara,
sistem astatic)
(eroare stationara,
sistem astatic)
Performante de regim tranzitoriu:
![]() (timp de raspuns, timp
de reglare)
(timp de raspuns, timp
de reglare)
![]() (suprareglaj)
(suprareglaj)
![]() (grad de amortizare)
(grad de amortizare)
c) Pentru ξ=1 (aperiodic):
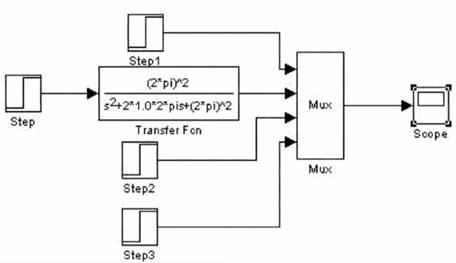
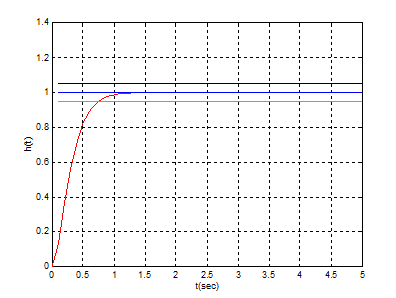
Performante de regim stationar:
![]() (valoare de regim
stationar)
(valoare de regim
stationar)
![]() (eroare stationara,
sistem astatic)
(eroare stationara,
sistem astatic)
Performante de regim tranzitoriu:
![]() (timp de raspuns, timp
de reglare)
(timp de raspuns, timp
de reglare)
![]() (suprareglaj)
(suprareglaj)
![]() (grad de amortizare)
(grad de amortizare)
d) Pentru ξ=3.0 (supraamortizat):
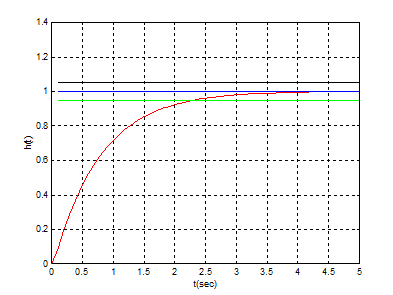
Performante de regim stationar:
![]() (valoare de regim
stationar)
(valoare de regim
stationar)
![]() (eroare stationara,
sistem astatic)
(eroare stationara,
sistem astatic)
Performante de regim tranzitoriu:
![]() (timp de raspuns, timp
de reglare)
(timp de raspuns, timp
de reglare)
![]() (suprareglaj)
(suprareglaj)
![]() (grad de amortizare)
(grad de amortizare)
2.6. Calculul caracteristicilor
logaritmice de frecventa unde U(ω), V(ω), A(ω), φ(ω),
U(ω)/V(ω) pentru T![]() =1(s) si ξ=0,707.
=1(s) si ξ=0,707.
Ecuatia:
![]() +2ξω
+2ξω![]()
![]() +ω
+ω![]() =k ω
=k ω![]()
![]() r(t)
r(t)
unde:
k=1
ω![]() =
=![]() =2π
=2π
r=1(t)
![]() (0)=y(0)=0
(0)=y(0)=0
Aplicam transformata directa Laplace:
s![]() Y(s)+ 2ξω
Y(s)+ 2ξω![]() sY(s)+ ω
sY(s)+ ω![]() Y(s)= ω
Y(s)= ω![]()
![]() R(s)
R(s)
Deducem functia de transfer:
s![]() Y(s)+ 2ξω
Y(s)+ 2ξω![]() sY(s)+ ω
sY(s)+ ω![]() Y(s)= ω
Y(s)= ω![]()
![]() R(s)
R(s) ![]()
s![]()
![]() +2ξω
+2ξω![]() s
s![]() + ω
+ ω![]()
![]() = ω
= ω![]()
![]()
G(s)=![]()
Facem substitutia s=jω:
W(jω)=
![]() =
=![]() =
=![]() =
=
= ω![]()
![]() -j ω
-j ω![]()
![]()
W(jω)=A(ω)e![]() =U(ω)+jV(ω)
=U(ω)+jV(ω)
U(ω)=
ω![]()
![]() =4π
=4π![]()
![]()
V(ω)=-
ω![]()
![]() =-4π
=-4π![]()
![]()
A(ω)=![]() =
= 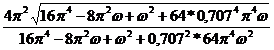
φ(ω)=arctg![]() =arctg(-
=arctg(-![]() )=-arctg
)=-arctg![]()
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |