
Utilizarea distributiei Dirac pentru deducerea caracteristicilor spectrale

![]()
Relatiile de definitie sunt:
![]()
![]()
sau daca t0 = 0
![]()
Proprietati:
Distributia δ se considera para
δ (t-τ) = δ (τ- t);
2. Proprietatea de " sondare in timp ":
Se considera un semnal u(t)
![]() ;
;
Este o consecinta directa a relatiei de definitie .
" Sondarea in frecventa " :
Fie caracteristica spectrala U(jω). Se considera aceasta caracteristica spectrala la frecventa ω0 .
![]() .
.
u(t)δ(t-t0)
= u(t0)δ(t-t0), ![]() ;
;
5. Derivata distributiei Heaveside
Daca u(t) reprezinta distributia Heaveside sau treapta unitara, avem:
![]() ;
;
6. Transformata Fourier a distributiei δ :
F = ![]() δ(t)e-jωtdt = e-jω.0
=1 (vezi proprietatea de sondare) .
δ(t)e-jωtdt = e-jω.0
=1 (vezi proprietatea de sondare) .
7. Fie 2πδ(jω) o distributie definite in domeniul frecventelor. Sa se calculeze F-1 = ? .
F ![]()
![]() 2πδ(jω)ejωtdω= e0.t
= 1.
2πδ(jω)ejωtdω= e0.t
= 1.
Consecinta: Transformata Fourier directa va fi:
![]()
In general , rezultatul incadrat poate fi scris in felul urmator:
F = 2πAδ(jω); daca u(t) = A (semnal continuu).
Caracteristica spectrala a unui semnal constant de amplitudine A este data de o componenta de frecventa zero, a carei densitate este infinita.
8. Caracteristica spectrala a unei functii exponentiale de forma ejω0t nu are transformata Fourier.
![]()
Theorema deplasarii spectrale: ![]()
9. Caracteristicile spectrale ale functiilor trigonometrice
cos ω0t = (ejω0t + e-jω0t ) / 2;
F = ![]() [ F + F ] = π
[ F + F ] = π
sin ω0t = (ejω0t - e-jω0t ) / 2j ;
F = ![]()
![]()
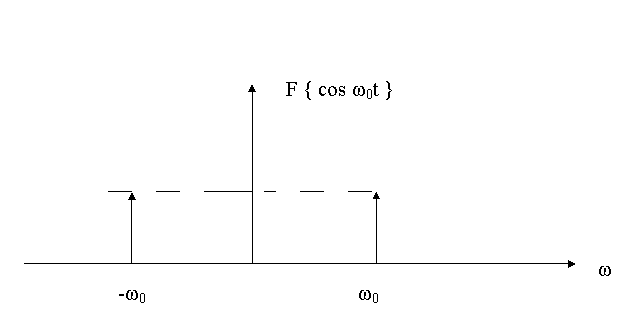
Factorul 1/j nu afecteaza decat caracteristica de faza , aratand ca fata de cazul anterior exista doar diferente de faza .
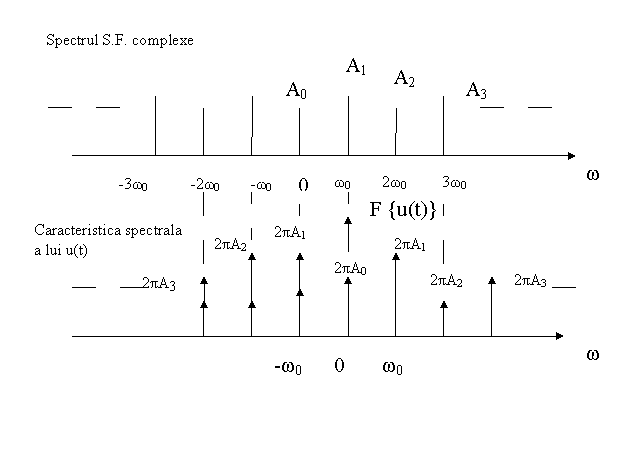
10. Determinarea caracteristicilor spectrale ale unui semnal periodic :
![]() u(t) =
u(t) = ![]() Ai ejiω0t
Ai ejiω0t
![]()
![]() F
=
F
= ![]() AiF = 2π
AiF = 2π ![]() Ai δ[j(ω-iω0)]
Ai δ[j(ω-iω0)]

SEMNALE ESANTIONATE
Achizitia semnalelor in calculator se face prin convertoare analog numerice (A/N). Acestea realizeaza doua operatii:
Dintre cele doua operatii esantionarea este mult mai deosebita (timp discret).
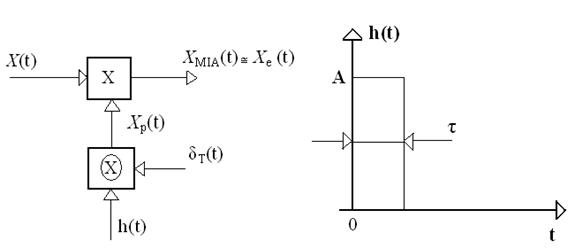
Un esantionator se reprezinta schematic astfel:
 unde:
x(t) - semnalul care trebuie esantionat
unde:
x(t) - semnalul care trebuie esantionat
xe(t) - semnalul esantionat
Esantionare ca modulatie a impulsurilor in amplitudine (MIA) :
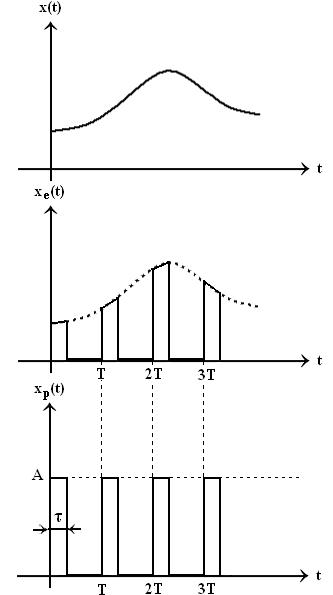
Pentru inceput putem trata esantionarea ca o MIA. Vom presupune ca impulsurile sunt unitare, adica Aτ = 1. In continuare vom deduce modelul matematic al semnalului esantionat tratat ca semnal MIA.
O prima operatie este modelarea semnalului purtator a lui xp(t)
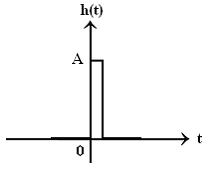
Sa consideram o functie.
Vom calcula convolutia h(t)![]() δT(t).
δT(t).
δT(t) = ![]() (functie pieptene)
(functie pieptene)
h(t)![]() δT(t) = h(t)
δT(t) = h(t) ![]()
![]() =
= ![]() = xp(t).
= xp(t).
Cand i = 0 → u(t)
![]()
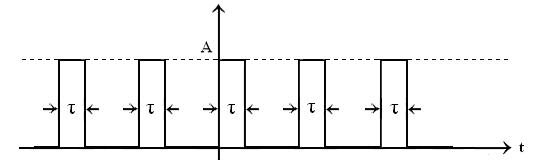
Cand i = 1 → u(t - T)
Cand i = 2 → u(t - 2T)
Pentru i negativ : h(t)![]() δT(t).= xp(t)
δT(t).= xp(t)
![]()
Xe(t)=XMIA(t)=Xp(t) X(t) ;
Ne intereseazǎ caracteristica spectralǎ a impulsurilor modulate in amplitudine.
XMIA(jω)=F F=![]() Xp(jω)
Xp(jω)![]() X(jω) ;
X(jω) ;
Calculul Xp(jω):
Xp(t)=h(t)![]() δT(t)
δT(t)![]() F F
F F![]() Xp(jω)=F F
Xp(jω)=F F
Calculam mai intai transformata Fourier a distributiei δ periodicǎ , adicǎ a functie δT(t)
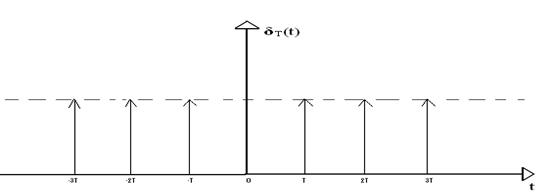
Fiind un semnal periodic δT(t) se poate descrie printr-o serie Fourier complexǎ de forma:
T(t)=![]() i .
i .![]()
![]()
![]() ,cu ω0=
,cu ω0=![]() ;
;
![]() i=
i=![]() .
.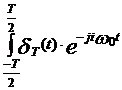 dt=
dt=![]()
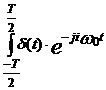 dt=
dt=![]()
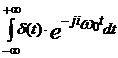 =
=![]() .
.![]() =
=![]()
Revenind la seria Fourier complexǎ avem:
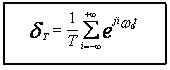
![]()
Calculǎm transformata Fourier:
F=![]()
![]() F=
F=![]()
![]() =
=![]()
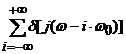
Caracteristica spectralǎ este deci:
![]()
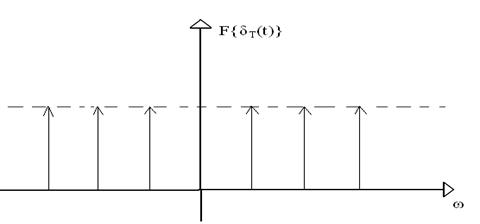
![]() Notǎm cu
Notǎm cu
![]() (j
(j![]() )
)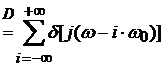
distributia
![]() periodicǎ definitǎ pe scara frecventelor
periodicǎ definitǎ pe scara frecventelor
![]()
Calculǎm acum:
H(j![]() )=F
)=F
In exemplul tratat in cursul trecut, am calculat transformata Fourier pentru functia:
F(jω)=F=Aτ
sinc![]()
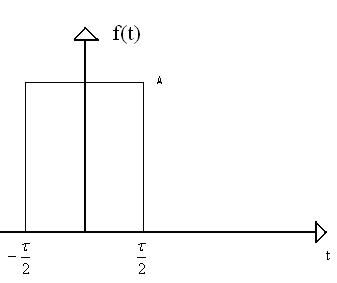
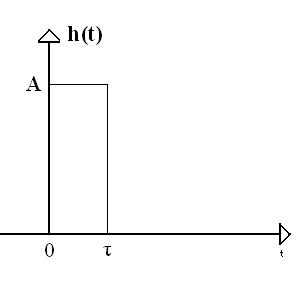
Constatǎm
ca h(t)=f(t-![]() ).
).
Aplicand
teorema intarzierii![]() H(jω)=
H(jω)=![]() ;
;
Revenim
la calculul lui ![]() (jω) :
(jω) :
![]() (jω)=A
(jω)=A![]()
![]() , cu
, cu 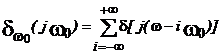 ;
;
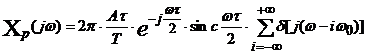 ;
; ![]()
Am studiat proprietatea: ![]() ;
;
Aplicand
aceastǎ proprietate egalitatii ![]() obtinem:
obtinem:
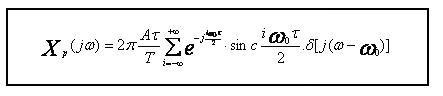
Caracteristica spectralǎ a semnalului ![]() (t) este deci:
(t) este deci:
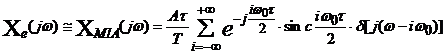
![]()
![]()
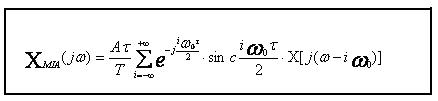
Vom
presupune ca A![]() si ca semnalul x(t) are spectrul alaturat:
si ca semnalul x(t) are spectrul alaturat:
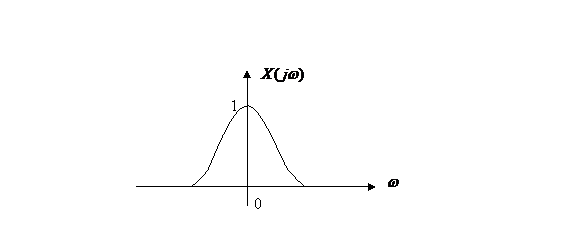
Din formula (1) rezulta urmatoarea caracteristica spectrala a semnalului xMIA(t):
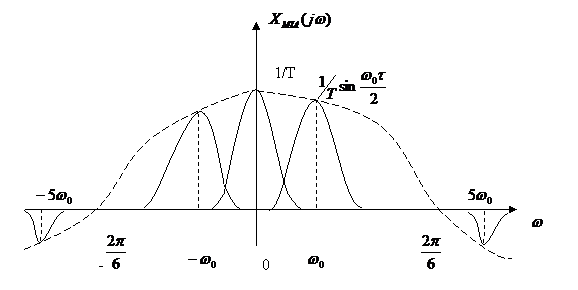
S-a considerat ca pentru i=4 avem:
![]()
![]()
Modelul matematic al procesului de esantionare ideal
Se
constata ca ![]()
![]()
![]()
In
aceasta situatie avem: ![]()
![]() fiind semnalul
esantionat ideal. Din formula (1), pentru
fiind semnalul
esantionat ideal. Din formula (1), pentru ![]() , rezulta caracteristica spectrala
, rezulta caracteristica spectrala ![]() .
.
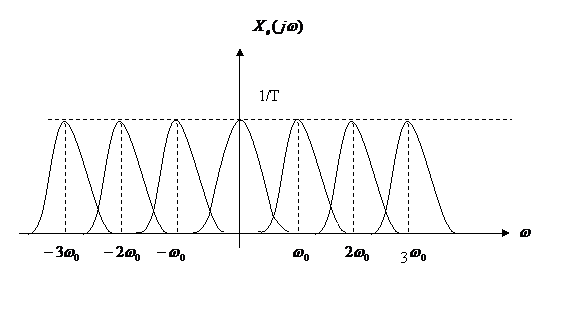
Modelul esantionatorului ideal este deci:
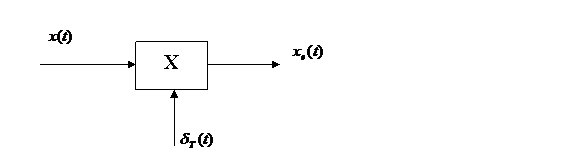
![]()

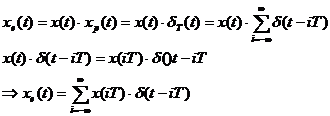
Determinam caracteristica spectrala a semnalului esantionat ideal, plecand de la relatia:
![]()
careia ii aplicam transformata Fourier:
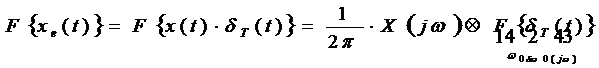
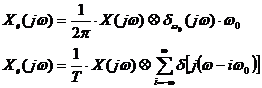
Datorita
proprietatii de sondare in frecventa a functiei ![]() , avem:
, avem:
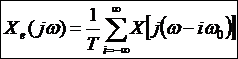 (3)
(3)
Constatam ca relatia (3) se poate obtine din (1) prin trecere la limita:
![]()
Semnalul esantionat are o
caracteristica spectrala in care caracteristica spectrala a
semnalului de baza este distribuita periodic pe axa frecventelor
cu perioada ![]()
![]() = pulsatie de
esantionare
= pulsatie de
esantionare
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |