
CALCULUL LA STAREA LIMITA DE REZISTENTA AL ELEMENTELOR DE BETON ARMAT SOLICITATE LA TORSIUNE
1 Consideratii introductive
Solicitarea la torsiune apare in structurile de beton armat ca urmare a continuitatii dintre elemente (fig.1.71 a si b). Legatura rigida dintre grinda secundara si grinda principala din figura 71a face ca rotirea din incovoiere a grinzii secundare sa fie egala cu rotirea de rasucire a grinzii principale; ca urmare, grinzii principale i se aplica un moment de torsiune egal cu cel de incovoiere de la capatul grinzii secundare (fig. 1.71.b). Datorita insa faptului ca valorile rigiditatilor la rasucire ale elementelor de beton armat (in special in stadiul fisurat) sunt foarte reduse in raport cu cele la incovoiere, momentele de torsiune au de multe ori valori foarte mici. In consecinta la structurile al caror echilibru este posibil si fara considerarea rigiditatilor la torsiune acestea sunt, de regula, negljate in calcul.
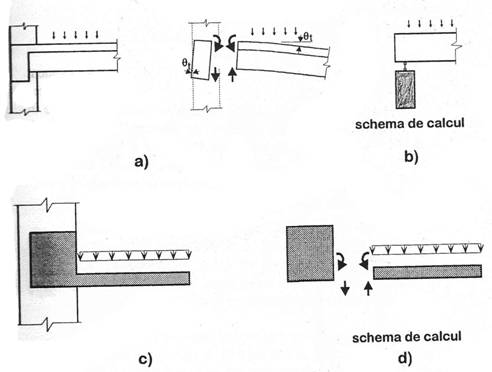
FIGURA 1.71
Exista si situatii in care solicitarea la torsiune insoteste nemijlocit splicitarea la incovoiere in asigurarea echilibrului general al unui subansamblu. De exemplu, echilibrul placii copertinei din fig.1.71.c si d, nu poate fi realizat decat prin incastrarea in grinda solicitata la torsiune.
Solicitarea la torsiune este insotita si de solicitarea la incovoiere cu forta taietoare. Sub actiunea combinata a acestor eforturi, elementul de beton armat, in stadiul de cedare, prezinta o sectiunea stramba de rupere (fig.1.72):
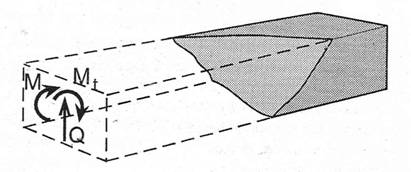
FIGURA 1.72
Asigurarea fata de ruperea dupa o astfel de sectiune implica satisfacerea simultana a urmatoarelor conditii pentru starea limita de rezistenta:
Mi <Mlcap
M <Mcap
Q <Qcap
unde MUcap, Mcap si Qcap reprezinta rezultantele moment de torsiune, moment incovoietor si forta taietoare ale eforturilor pe sectiunea stramba la epuizarea capacitani sale de rezistenta, iar Mt, M si Q eforturile sectionale respective in calculul la starea limita de rezistenta. Ruperea intervine ca urmare a epuizarii capacitatii betonului comprimat dup ace in prealabil betonul a fisurat, iar armaturile longitudinale si trasversale au ajuns la curgere (fig. 1.73).
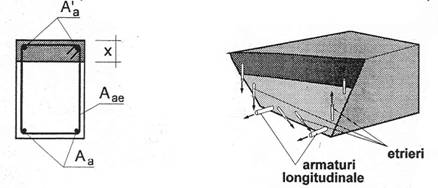
FIGURA 1.73
Din cauza dificultatii de a
considera simultan efectul actiunii celor trei categorii de eforturi in
momentul cedarii, in multe prescriptii de proiectare, exclusiv cele din
Se poate demonstra ca intre valoarea mai aproximativa (dar acoperitoare) a momentului capabil la torsiune stabilita pe baza modelului de grinda zabrele si valoarea mai riguroasa stabilita pe baza echilibrului limita in sectiuni strambe sunt diferente neinsemnate. Aceasta concluzie este confirmata si de studiile experimentale.
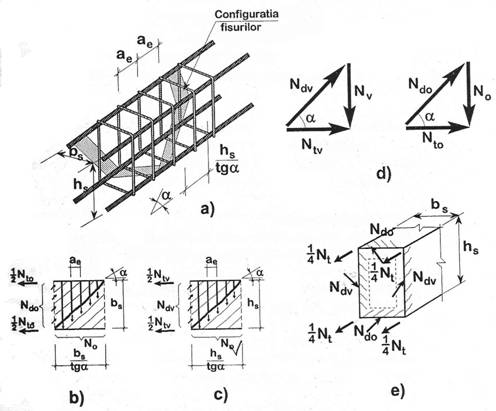
FIGURA 1.74
2. Dimensionarea elementelor solicitate la torsiune pe baza modclului de grinda cu zabrele
Daca se considera o fisura potentiala de rupere cu inclinarea ά, aceasta intercepteaza pe o fata verticala a grinzii nν = hs/aetgά ramuri verticale ale etrierilor (fig. 1.74b).
Rezulta ca la starea limita de rezistenta, forta de intindere totala dezvoltata in acesti etrieri este:
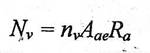
(1.135.a)
Similar forta de intindere totala dezvoltata in etrierii interceptati de fisura de rupere pe o fata orizontala a grinzii este:
![]() (1.135.b)
(1.135.b)
no = bs/aetgά, numarul de ramuri de etrier care traverseaza fisura marcata pe
fata orizontala a elementului (fig. 1.74.a).
La nodurile grinzii cu zabrele spatiale eforturile din etrieri se echilibreaza cu eforturile din talpile intinse si cu eforturile din diagonalele comprimate de beton constituite intre flsurile inclinate (fig.1.74.b, c, d, e). Cu notatiile definite in aceste figuri rezulta:
. eforturile din diagonalele comprimate, insumate pe laturile elementului :
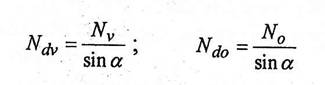
(1.136)
. forta orizontala totala din talpi, egala cu proiectiile pe orizontala ale eforturilor din diagonalele comprimate de beton intr-o sectiune verticala prin grinda :
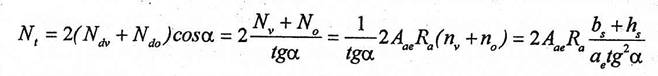
Daca se noteaza cu Atl aria totala a armaturilor longitudinale se obtine:
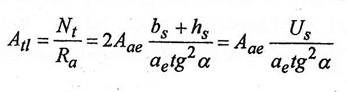
(1.138)
in care Us=2(bs + hs ) este perimetrul miezului de beton (cuprins la interiorul etrierilor) in sectiunea transversala.
Fortele din etrieri sunt transmise in nodurile grinzii cu zabrele spatiale prin mtennediul celor 4 bare longitudinale de la colturi (fig.1.74.e). Configuratia fortelor diagonale de compresiune Ndv si Ndo intr-o sectiune transversala este mdicata in fig.1.74.d. Componentele din planul sectiunii transversale ale acestor forte echilibreaza momentul de torsiune aplicat sectiunii:
Mt = (Ndvbs + Ndohs) sin ά = Nvbs + Nohs
Explicitand valorile eforturilor din etreri rezulta:
(1.139)
in care Abs = bshs reprezinta aria sectiunii samburelui de beton din interiorul etrierilor.
Daca admitem ά = 45°, respectiv ca fisurile se dezvolta dupa traiectoriile eforturilor principale de compresiune in conditiile torsiunii pure pentru elemente din materiale omogene si elastice, relatiile de dimensionare ale armaturilor transversale si longitudinale devin:
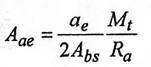
(1.140)
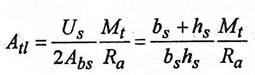
(1.141)
Observatii:
a) In demonstratia expresiilor de calcul s-a considerat ca armatura longitudinala este alcatuita din 4 bare dispuse la colturile sectiunii. Cercetarile experimentale au evidentiat faptul ca modul concret in care este distribuita armatura longitudinala nu are practic importanta daca aceasta prezinta o configuratie simetrica si daca este corespunzator ancorata dincolo de sectiunea in care se aplica momentul de torsiune.
Armatura longitudinala fiind solicitata la intindere rezulta ca dupa fisurarea inclinata, elementul torsionat se alungeste. In consecinta, orice cauza care se impotriveste acestei alungiri (inclusiv precomprimarea) are un efect favorabil.
b) O transmitere corespunzatoare a fortelor la 'nodurile' grinzii cu zabrele spatiale necesita:
- o buna ancorare a etrierilor, dincolo de central teoretic al nodului. In acest scop etrierii pentru preluarea torsiunii se realizeaza cu o forma specifica
(fig.1.75);
- un diametru suficient al armaturii longitudinale din colturi, pentru a reduce eforturile locale in beton; se recomanda ca diametral armaturii longitudinale din colturi sa fie cel putin ae/10.
c) Analiza comportarii grinzii cu zabrele spatiale, ca si cercetarile experimentale evidentiaza faptul ca elementele cu sectiune plana si cele tubulare, la un contur perimetral si armare identice, au aceeasi capacitate de rezistenta. Aceasta constatare este valabila atata vreme cat peretele sectiunii tubulare nu este prea subtire, incat sa se ajunga la ruperi ale diagonaleior de beton la compresiune.
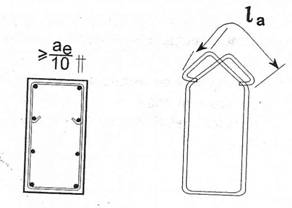
FIGURA 1.75
Din fig.1.74.e, se constata ca zona de beton aflata la interior (delimitata prin linie intrerupta) nu este mobilizata in mecanismul de rezistenta al grinzii spatiale cu zabrele.
d) Se poate demonstra ca solutia de armare cea mai economica se obtine atunci cand volumul annaturilor Iongitudinale este egal cu volumul armaturilor transversale.
Pe baza relatiei (1.138) rezulta:
Se constata ca aceasta conditie corespunde lui = 45°, ceea ce confirma ipoteza facuta anterior in legatura cu stabilirea relatiilor (1.140) si (1.141).
3. Actiunea combinata a fortei taietoare si a momentului de torsiune
Actiunea momentului de torsiune insoteste, de regula, actiunea fortei taietoare. Valoarea teoretica a efortului unitar principal de intindere (egal in axa neutra cu valoarea efortului unitar tangential) este:
σI = τ = τq + τMt (1.143)
in care:
τq = Q/bho, este efortul unitar tangential provenit din actiunea fortei taietoare;
τMt efortul unitar tangential produs de actiunea momentului de torsiune.
Asa cum s-a aratat la 1.3.1, efortul unitar tangential astfel calculat are un caracter conventional si trebuie interpretat ca un indice al nivelului de solicitare la eforturi de forfecare.
In functie de valoarea stabilita cu relatia (1.143) pot interveni urmatoarele cazuri:
≤ 0,5 Rt solicitarea este sub cea care produce fisurarea inclinata, situatie in care armatura din inima nu rezulta necesara din calcul, ea dispunandu-se pe baza regulilor de armare minima;
Rt < τ ≤ 4Rt cazul in care armatura transversala rezulta din calcul, fara sa se depaseasca rezistenta diagonaleior comprimate (efortul unitar principal de compresiune ramane inferior rezistentei la compresiune in regim de solicitare biaxiala);
- τ > 4Rt, cand exista riscul ruperii la compresiune in sectiuni inclinate si sectiumea de beton trebuie sporita.
Pentru calculul valorilor τMt din expresia (1.143) se pot folosi relatiile matoare, stabilite in rezistenta materialelor:
. in cazul sectiunilor dreptunghiulare:
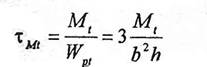
(1.144)
S-a nbtat cu Wpt, modulul de deformatie la torsiune in domeniul postelastic.
. in cazul sectiunilor compuse care se pot asimila cu sectiuni alcatuite din mai multe dreptunghiuri (fig.1.76.a):
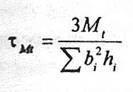
(1.145)
in care indicele i se refera la dreptunghiul i din alcatuirea sectiunii.
in cazul sectiunilor chesonate (sectiimi inchise cu pereti subtiri):
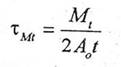
(1.146)
S-a notat:
Ao = aria delimitata de linia mediana a peretelui tubului (hasurata in fig.1.76.b);
t = grosimea peretelui.
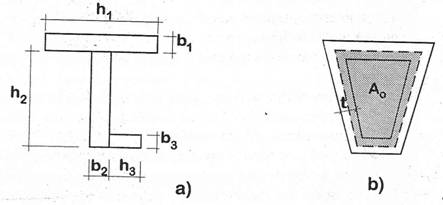
FIGURA 1.76
4. Aspecte ale solicitarii compuse incovoiere-torsiune
La pct.2 s-au prezentat dificultatile legate de evaluarea capacitatii de rezistenta la solicitarea de incovoiere cu torsiune pe suprafetele strambe de rupere.
Dezvoltand modelul de grinda cu zabrele pentru solicitarea la incovoiere cu torsiune se poate deduce o lege aproximativa, de tip parabolic, pentru curba de interactiune limita moment de incovoiere - moment de torsiune (fig.1.77):
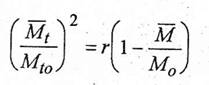
(1.147)
pentru cazul in care ruperea este asociata cu solicitarea la curgere a armaturii din zona intinsa si:
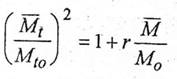
(1.148)
cand armatura din zona supusa la compresiune de momentul incovoietor este solicitata la curgere prin intindere in momentul ruperii:
S-a notat:
M,Mt, = momentele de incovoiere si de torsiune la ruperea elementului;
Mo,Mto = momentele capabile la incovoiere pura si la torsiune pura;
Relatiile (1.147) si (1.148) sunt in buna concordanta cu rezultatele cercetarilor experimentale.
Daca armarea este simetrica (Aa = Aa') la rupere curge totdeauna armatura din zona intinsa de momentul M in care se insumeaza eforturile de intindere provenite atat din incovoiere, cat si din torsiune, in timp ce in armatura de la extremitatea opusa a sectiunii cele doua eforturi se scad. Din fig.1.73 se constata ca pentru acest caz de armare actiunea unuia din cele doua eforturi reduce capacitatea de rezistenta la celalalt efort, in raport cu conditiile de solicitare la incovoiere sau torsiune pura.
In cazul armarii nesimetrice, in intervalul de valabilitate al relatiei (1.148), se constata ca la valori reduse ale momentului incovoietor, momentul capabil la torsiune sporeste fata de situatia de solicitare la torsiune pura, ca urmare a faptului ca pentru curgerea prin intindere a armaturii Aa', trebuie compensata in prealabil compresiunea din aceasta armatura produsa de momentul incovoietor.
In proiectarea curenta, asa cum s-a aratat, se adopta solutia mai sirnpla, cu caracter acoperitor de a dimensiona separat annaturile necesare pentru preluaiea incovoierii si separat armaturile pentru acoperirea momentului de torsiune si de a le dispune insmnate in elemental de beton armat.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |