
MECANICA ANALITICA
Notiuni introductive:
In capitolele precedente s-a studiat miscarea sistemelor
de puncte materiale sub actiunea unor forte exterioare efectiv aplicate sau de
legatura si a unor forte interioare, folosind principiile lui
Ne reamintim ca problema centrala a
Mecanicii clasice ce a trebuit rezolvata a fost urmatoarea: sa se studieze
miscarea, intr-un interval de timp a unui sistem de puncte materiale. Mi(i=1÷n),
de mase mi si vectori de pozitie ![]() i(t) actionate de fortele
i(t) actionate de fortele ![]() i(t ,
i(t ,![]() i ,
i ,![]() i) exterioare si interioare si supus unor
legaturi. Sistem material a
carui stare in momentul initial este cunoscuta (adica sunt cunoscuti vectorii
i) exterioare si interioare si supus unor
legaturi. Sistem material a
carui stare in momentul initial este cunoscuta (adica sunt cunoscuti vectorii ![]() oi si vectorii viteza
oi si vectorii viteza ![]() oi
oi
Pentru rezolvarea acestei probleme au fost enuntate teoriile generale ale dinamicii: teorema impulsului, teorema momentului cinetic si teorema energiei cinetice si a lucrului mecanic. Desi fortele interioare sunt totdeauna eliminate de primele doua teoreme si in multe cazuri si de cea de-a treia, utilizarea teoremelor generale prezinta complicatii de scriere si de rezolvare a sistemelor de ecuatii diferentiale ale mecanicii, in special pentru sistemele mecanice cu un numar mare de grade de libertate, datorita urmatoarelor motive:
In sistemul de ecuatii obtinut prin utilizarea teoremelor generale raman ca necunoscute fortele de legatura din legaturile sistemului cu mediul exterior ;
Complicarea teoremelor generale conduce la sisteme de ecuatii diferentiale foarte diferite de la o problema la alta, un studiu unitar al proprietatilor generale ale miscarii mecanice fiind greu de realizat.
In aceste conditii a aparut avantajos sa se reformuleze problemele de Mecanica clasica intr-o forma mai generala si sa se stabileasca principiile analitice ale mecanicii. La baza principiilor analitice ale mecanicii stau tot legile fizice ale acestei stiinte, principiile analitice constituind exprimarea sub forma matematica a acestora.
Mecanica privita sub acest aspect theoretic se numeste Mecanica analitica, nume dat de J.L.Lagrange. Mecanica analitica isi propune sa stabileasca metode directe de determinare a ecuatiilor de miscare in care sa nu apara fortele de legatura si sa se exprime acest sistem de ecuatii sub forma generala (forma canonica), aceeasi oricare ar fi problema de mecanica studiata. Mentionam ca in Mecanica analitica, legaturile se considera ideale.
Acest mod de abordare a studiului miscarii sistemelor de puncte si corpuri materiale a permis formularea unor principii analitice care in functie de metode matematice utilizate se pot clasifica in: principii diferentiale si principii integrale.
Principiile diferentiale studiaza fenomenul mecanic la un moment dat, considerand variatii de timp si de spatiu elementare. Cele mai inportante dintre aceste principii sunt: principiul lucrului mecanic virtual, principiul lui D'Alambert, principiul lui Gauss(principiul celei mai mici constrangeri).
Principiile integrale examineaza fenomenul mecanic intr-un interval
finit de spatiu si de timp, reducand problema la gasirea unor valori care fac
stationare anumite integrale. Aceste principii sunt: principiul lui
In continuare se vor studia pe larg acele principii si metode ale mecanicii analitice cu o larga aplicatie in practica profesiei de inginer constructor si anume: principiul lui D'Alambert, principiul lucrului mecanic virtual, ecuatiile lui Lagrange.
Coordonate generalizate. Viteze generalizate
In mecanica newtoniana, pozitia unui sistem finit de puncte materiale Mi(i=1÷n) este definita in spatial euclidian cu trei dimensiuni prin 3n marimi:
x1y1z1 , x2y2z2 ,..., xnynzn (1)
numite coordonate carteziene ale sistemului de puncte.
Mecanica analitica inlocuieste spatial euclidian cu trei dimensiuni ale fenomenelor fizice cu un spatiu mai general, multidimensional. Sirul (1) poate fi scris astfel:
x1 , x2 , x3 , ....., x3n (2)
sau inlocuit cu 3n parametrii :
q1 , q2 , q3 , ....., q3n (3)
presupunand in acest caz ca intre sirurile (1) si (3) exista corespondenta:
q3i-2=xi ; q3i-1=yi ; q3i=zi .
Sub aceasta forma cele 3n coordonate carteziene ale sistemului (Mi) pot fi considerate 3n coordonate ale unui punct reprezentativ M al sistemului, intr-un spatiu cu 3n dimensiuni.
In general, un sistem de puncte materiale este supus la legaturi. Se presupune ca numarul de legaturi este l si ca acestea se exprima prin l relatii de de forma:
Fj(x1 , x2 ,...., x3n , t)=0 ; (j=1,2,3,...,l) (4)
In aceste conditii se pot exprima toate cele 3n coordonate in functie de k parametrii independenti q1 , q2 , ....., qk ; (k=3n-l) ; astfel incat relatiile (4) sa fie identic satisfacute, deci:
xi=xi(q1 , q2 , ... , qk , t)
Sau (5)
![]() i=
i=![]() i(q1 , q2 , .. , qk
, t).
i(q1 , q2 , .. , qk
, t).
Intr-un sens mai larg, cei k parametrii: q1, q2, ...., qk pot fi considerati ca fiind coordonatele sistemului de puncte materiale si se numesc coordinate generalizate. Relatiile (5) reduc problema determinarii pozitiei la un moment dat al sistemului (Mi) din spatiul Euclidian cu trei dimensiuni, la determinarea pozitiilor unui singur punct figurativ in spatiul coordonatelor q avand k dimensiuni. Acest spatiu se numeste spatiul configuratiilor sau spatiul figurativ sau spatiul Lagrange.
Succesiunea de valori luate in timp de parametrii q fac cunoscuta "traiectoria" punctului figurativ in spatiul configuratiilor, determinate prin ecuatiile:
qj=qj(t); (j=1,2,...,k). (6)
Daca este cunoscuta miscarea
punctului figurativ se cunoaste si miscarea sistemului de puncte materiale. Se
spune prin analogie ca marimile ![]() j (j=1,2,3,4,...,k) reprezinta vitezele
generalizate (reprezinta proiectiile vitezei punctului figurativ pe "axele"
spatiului configuratiilor).
j (j=1,2,3,4,...,k) reprezinta vitezele
generalizate (reprezinta proiectiile vitezei punctului figurativ pe "axele"
spatiului configuratiilor).
Legaturi. Clasificarea legaturilor.
Datorita faptului ca Mecanica analitica a aparut si din necesitatea eliminarii fortelor de legatura din ecuatiile de miscare in continuare se prezinta cateva aspecte specifice ale problemei legaturilor si al modului de tratare al acestora in Mecanica analitica, mod diferit de cel al Mecanicii clasice.
Notiunea de legatura, introdusa inca din partea de Statica a acestui curs, exprima o obligatie de natura geometrica impusa unuia sau mai multor puncte ale unui sistem material. Aceste constrangeri geometrice presupun o limitare a pozitiilor punctelor materiale ce alcatuiesc sistemul. Exprimarea analitica a acestor conditii poate fi facuta si sub forma finita (ca relatii intre coordonate), fie sub forma diferentiala (ca relatii intre deplasari). De exemplu, obligatia unui punct material M(x,y,z) de a ramane pe o suprafata f(x,y,z)=0 se poate exprima astfel:
Prin conditia impusa coordonatelor punctului sa satisfaca ecuatia suprafetei:
F(x,y,z)=0; (7)
Prin conditia de deplasarea infinitesimala a punctului, d![]() , sa satisfaca relatia diferentiala:
, sa satisfaca relatia diferentiala:
![]() +
+![]() +
+![]()
![]() (8)
(8)
In acest caz particular, rel.(8) poate fi obtinuta din (7) fiind diferentiala totala a acesteia, asa cum rel.(7) poate fi dedusa prin integrare.
Intr-un caz general, relatia
diferentiala ce trebuie satisfacuta de deplasarea infinitesimala d![]() este de forma:
este de forma:
F1(x,y,z)dx+F2(x,y,z)dy+F3(x,y,z)dz=0 (9)
Daca e posibil ca prin diferentierea unei relatii intre coordonate sa se obtina o relatie intre deplasarile infinitesimale dx,dy,dz, procesul invers de obtinere a unei relatii intre coordonatele x,y,z, prin integrarea relatiei (9) poate fi rezolvat numai daca aceasta este o diferentiala totala exacta caz in care sunt satisfacute relatiile:
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() . (10)
. (10)
Relatiile (10) exprima conditia ca functiile F1, F2 si F3 sa fie derivatele partiale ale unei functii f(x,y,z) in raport cu coordonatele x,y,z, astfel:
F1=![]() ; F2=
; F2=![]() ; F3=
; F3=![]() .
.
Deoarece forma diferentiala este mai generala decat forma intreaga, studiul legaturilor se efectueaza pe forma diferentiala. Din acest punct de vedere, legaturile se clasifica in mai multe categorii ce vor fi prezentate in continuare:
Legaturile olonome sunt acele legaturi la care forma diferentiala este integrabila, iar numarul gradelor de libertate ale sistemului pentru deplasari finite este egal cu numarul gradelor de libertate pentru deplasari infinitesimale; se exprima prin relatii intre coordonate, de forma: f(x,y,z)=0 sau f(x,y,z,t)=0 sau f(q1,q2,...,qn,t)=0.
Legaturi neolonome sunt legaturile la care forma diferentiabila este neintegrabila, iar numarul gradelor de libertate al sistemului pentru deplasari finite este mai mare decat numarul gradelor de libertate pentru deplasari infinitesimale; se exprima prin relatii de forma:
![]() (
(![]()
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)![]()
sau
![]() (
(![]()
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)![]()
sau
![]() (
(![]() 1,
1, ![]() 2,...,
2,..., ![]() n,
n, ![]() 1,
1,![]() 2,...
2,...![]() n,
n, ![]() 1,
1,![]() 2,....,
2,....,![]() n,
n, ![]() )
)![]()
Legaturi critice sunt exprimabile prin forme diferentiale la care numarul de grade de libertate pentru deplasari finite este mai mic decat numarul gradelor de libertate pentru deplasari infinitesimale.
In Mecanica analitica, legaturile se clasifica si in functie se independenta sau dependenta lor de timp. Din acest punct de vedere, legaturile pot fi:
Legaturi scleronome- independente de timp, deci timpul nu apare implicit in forma lor de exprimare f(x,y,z)=0 sau f(q1,q2,...qn)=0;
Legaturi reonome- dependente de timp, deci sunt de forma f(x,y,z,t)=0 sau f(q1,q2,....qn,t)=0 ;
Problemele tratate in acest curs presupun legaturile ca fiind olonome-scleronome(de exemplu, un punct obligat sa se deplaseze pe o suprafata fixa sau pe o curba fixa).
Deplasarea virtuala
Anterior s-a aratat ca forma cea mai genarala de definire a unei legaturi este forma diferentiala in care intervin coordonatele punctelor si deplasarile lor infinitesimale. In cazul legaturilor reonome intervin si timpul t respective dt.
Se considera un punct M supus unei legaturi scleronome, de exemplu obligat sa se gaseasca pe o suprafata fixa S (Fig. 1) avand ecuatia: f(x,y,z)=0.
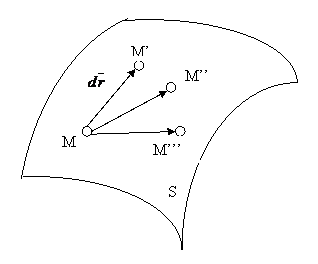
Fig.1.
Sub actiunea unor forte date punctul
M se deplaseaza in M', iar deplasarea infinitesimala ![]()
![]() se numeste deplasare
reala. Aceasta deplasare este continuta in planul tangent la suprafata si
satisface relatia:
se numeste deplasare
reala. Aceasta deplasare este continuta in planul tangent la suprafata si
satisface relatia:
![]() (11)
(11)
Sub actiunea unor forte punctul
poate efectua si alte deplasari (![]()
![]() ), tangente la suprafata, numite deplasari posibile. O
deplasare posibila reprezinta deci, orice deplasare compatibila cu legaturile,
deplasarea reala fiind una din deplasarile posibile.
), tangente la suprafata, numite deplasari posibile. O
deplasare posibila reprezinta deci, orice deplasare compatibila cu legaturile,
deplasarea reala fiind una din deplasarile posibile.
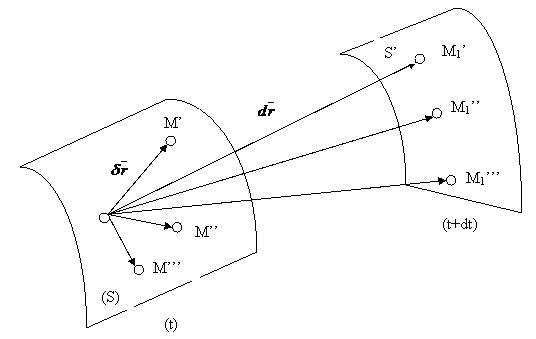
Fig.2.
Se considera punctul M supus unei legaturi reonome (fig.2) de exemplu obligat sa se gaseasca pe o suprafata (S) mobila sau deformabila in intervalul de timp de la t la t+dt.
DESEN:
In acest
interval de timp, sub actiunea unor forte date, mobilul M ajunge in punctual M'1,
deplasarea reala fiind ![]()
![]() 1. deplasarile posibile sunt
1. deplasarile posibile sunt ![]() 1,
1, ![]() 1 etc, deplasari ce nu sunt continute in planul
tangent la suprafata. Consideram ecuatia suprafetei f(x,y,z,t)=0, proiectiile deplasarii reale
1 etc, deplasari ce nu sunt continute in planul
tangent la suprafata. Consideram ecuatia suprafetei f(x,y,z,t)=0, proiectiile deplasarii reale ![]() satisfac relatia:
satisfac relatia:
![]() (12)
(12)
In acest caz, deplasarea reala este una din deplasarile posibile, deplasarii compatibile cu legatura.
Deplasarea virtuala este una
din cele mai importante notiuni cu care opereaza Mecanica analitica. Pentru a
definii aceasta notiune se imagineaza, ca pentru un moment, suprafata S din
fig.2 ar ramane fixa. In acest caz, deplasarile infinitesimale ![]() ,
,![]() , etc, tangente la suprafata, se numesc deplasari virtuale si
se noteaza:
, etc, tangente la suprafata, se numesc deplasari virtuale si
se noteaza:
![]()
![]()
![]()
![]()
![]() .
.
Conditia de a fi tangente la suprafata S se exprima prin relatia:
![]()
![]()
![]() sau
sau ![]() (13)
(13)
Comparand relatiile (12) si (13) rezulta ca, in cazul legaturilor reonome , deplasarea reala (sau posibila) nu se gaseste printre deplasarile virtuale.
In cazul legaturilor scleronome,
f(x,y,z)=0, ![]() , si relatiile (11) si (13) au aceeasi forma. In aceste
conditii, deplasarea virtuala reprezinta una din deplasarile posibile.
, si relatiile (11) si (13) au aceeasi forma. In aceste
conditii, deplasarea virtuala reprezinta una din deplasarile posibile.
In concluzie, in cazul legaturilor
scleronome, deplasarea virtuala ![]()
![]() are urmatoarele
proprietati:
are urmatoarele
proprietati:
-este fictiva (imaginara);
-este posibila (compatibila cu legaturile);
-se produce in afara timpului (considerat un parametru arbitrar, constant);
-este infinitesimala.
Din punct de vedere matematic, prin ![]() se intelege un
operator diferential, la fel ca si
se intelege un
operator diferential, la fel ca si ![]() cu singura deosebire
ca
cu singura deosebire
ca ![]() nu opereaza asura
timpului t.
nu opereaza asura
timpului t.
In cazul unui sistem de puncte materiale Mi(i=1÷n), avand q1.q2,...,qj,...,qk coordonate generalizate, se poate scrie:
![]() i=
i=![]() i (q1,q2,...qk,t)
i (q1,q2,...qk,t)
![]() i=
i=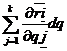 j
j![]() (14)
(14)
![]() i=
i=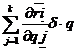 j (15)
j (15)
Unde ![]() I reprezinta vectorul de pozitie al unui punct
material Mi, iar
I reprezinta vectorul de pozitie al unui punct
material Mi, iar ![]() i si
i si ![]() i reprezinta deplasarea reala si deplasarea
virtuala ale acestui punct.
i reprezinta deplasarea reala si deplasarea
virtuala ale acestui punct.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |