Starea plana de tensiuni
Se considera ca in figura 1 un corp de forma unei placi cu grosimea constanta solicitata de un sistem de forte in echilibru actionand toate in planul median al placii. In aceasta situatie se poate admite ca tensiunile care apar in orice punct din corp sunt paralele cu planul placii, iar solicitarea placii este identica in toate planele paralele cu planul median.

O astfel de solicitare produce ceea ce se numeste stare plana a tensiunii. Daca placa ar fi fixata intre doi pereti rigizi, care sa-i impiedice deformatiile transversale, astfel ca deformatiile sa se produca numai in plane paralele cu planul median, s-ar putea vorbi de o stare plana de deformatii.
Cu ajutorul a trei plan perpendiculare pe planul placii, se izoleaza o prisma triunghiulara avand ca baza triunghiul dreptunghic OBC. Pe fetele elementului detasat vor actiona atat tensiuni normale σ cat si tensiuni tangentiale t. Raportand elementul la un sistem de axe rectangular xOy, tensiunile normale vor purta indicele axei cu care sunt paralele, iar tensiunile tangentiale vor avea doi indici, primul este indicele directiei proprii, iar al doilea, indicele directiei normale la planul in care acestea actioneaza.
Pa planul BC, facand unghiul a cu planul vertical OC, ambele tensiuni vor purta indicele a
Nontand cu dA aria suprafetei inclinate BC a elementului, ariile suprafetelor OB si OC vor fi dA sin a si dA cos a
Elementul detasat din placa va fi in echilibru sub actiunea fortelor care-l actioneaza, ca si placa. Se scrie o prima ecuatie de echilibru prin suma de momente fata de punctul D, unde rezultantele celor trei tensiuni σ se intersecteaza:
![]()
Rezulta:
txy tyx
adica legea paritatii sau dualitatii tensiunilor tangentiale.
Se scriu in continuare inca doua ecuatii de echilibru proiectand fortele pe directia tensiunilor σσ si τα :
a dA - σa dA cosa cosa - σy dA sina sin a txy dA sina cosa
tyx dAcosa sina
ta dA - σx dA cosa sina + σy dA dina cosa txy dA sina sina
+txy dA cosa cosa
Avand in vedere si legea paritatii (τxy = τyx) din ecuatiile obtinute pot fi exprimate tensiunile σa si τa de pe fata inclinata a elementului, in functie de tensiunile presupuse cunoscute, de pe fetele perpendiculare si in functie de unghiul de oblicitate a
a = σx cosa + σ sin2a txy sina cosa
ta = (σx - σy) sina cosa txy (cos2a - sin2a
Introducand unghiul dublu va rezulta,
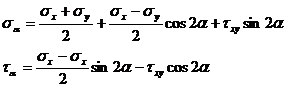 (1)
(1)
Tensiunile σa si ta, ca functii de unghiul a (1) pot sa ia valori maxime sau minime pentru anumite valori ale unghiului a. Astfel de valori ale unghiului a definesc asa zisele directii principale ale tensiunilor. Valorile maxime si minime ale tensiunilor poarta numele de tensiuni principale.
Directiile principale se obtin pe cale matematica prin anularea derivatelor relatiilor (1):
![]() (2)
(2) ![]() (3)
(3)
Relatia (2) va da:
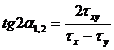 (4)
(4)
iar relatia (3)
 (5)
(5)
Ecuatiile (4) si (5) au cate doua solutii decalate intre ele cu 180o,
a a p ![]() ; (6)
; (6)
a a p ![]() (7)
(7)
Exista deci cate doua directii principale pentru fiecare din tensiunile σ si τ, directii formand intre ele un unghi drept. Dupa o directie principala tensiunea respectiva are valoarea maxima, iar dupa cea de-a doua, valoarea minima.
Din compararea relatiilor (1) si (2) se deduce,
![]() (8)
(8)
ceea ce arata ca in planele in care tensiunile normale sunt principale, tensiunile tangentiale lipsesc.
Din compararea relatiilor (4) si (5) se deduce,
tg2a tg2a
ceea ce insemneaza,
![]() sau
sau ![]() (9)
(9)
adica planele in care tensiunile tangentiale sunt maxime sau minime fac unghiuri de 45o cu planele in care tensiunile normale sunt principale.
Inlocuind in relatiile (1) unghiurile a date de relatiile (4) si (5) vor rezulta tensiunile principale sub forma,
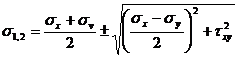 (10)
(10)
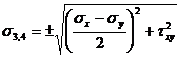 (11)
(11)
Relatiile (10) vor da,
σ1 + σ2 = σx + σy = const, (12)
ceea ce arata ca suma tensiunilor normale de pe doua plane perpendiculare, duse prin unul si acelasi punct, nu depinde de unghiul a, este un invariant.
Conform relatiilor (11) tensiunea tangentiala maxima este egala in valoare cu cea minima. Acest fapt este in concordanta cu legea dualitatii tensiunilor tengentiale.
Pe baza relatiei (10) se poate scrie,
![]() (13)
(13)
aceasta insemnand ca tensiunea tangentiala maxima este semidiferenta tensiunilor normale principale.
In fig. 2 sunt reprezentate tensiunile normale principale si directiile principale ale acestora in jurul unui punct oarecare. Considerand un element P in vecinatatea conturului, care se presupune neincarcat, pe fetele elementului vor lipsi tensiunile tangentiale. Ca urmare, directiile principale ale tensiunilor de contur vor fi normale si respectiv tangentiale la contur.

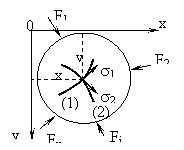
Fig. 2 Fig. 3
Pentru o stare plana de tensiuni se pot trasa o retea de linii tangente in toate punctele lor la tensiunile principale de solicitare. Acestea se numesc curbe izostatice si ele indica directia solicitarilor maxime si minime (fig. 3).
Ecuatia liniilor izostatice se obtine usor cu ajutorul relatiei (4):
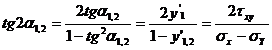
din care rezulta,
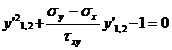
si solutiile,
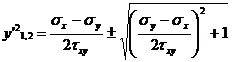 (14)
(14)
ceea ce reprezinta doua familii de curbe perpendiculare, deoarece,
![]()
Curbele tangente la tensiunile tangentiale maxime se numesc linii de lunecare. Ecuatia diferentiala a acestor linii se va obtine asemanator ca mai inainte, sub forma,
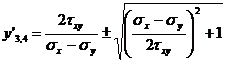 (15)
(15)
Relatiile (1) permit exprimarea tensiunilor σa si ta de pe o sectiune oarecare, intr-un punct, in functie de tensiunile principale.
Pentru aceasta trebuie, evident ca, σx = σ1, σy = σ2, txy
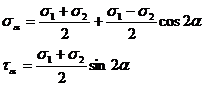 (16)
(16)
Eliminand unghiul 2a se obtine,
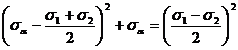 (17)
(17)
adica, in coordonate σa si τa, ecuatia unui cerc cu raza ½(σ1-σ2), cu centrul pe axa absciselor la distanta de origine 1/2( ). Aceasta poarta denumirea de cercul lui Mohr pentru starea plana de tensiuni (fig. 4).
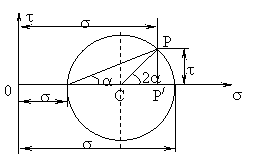
Fig. 4
Cu ajutorul reprezentarii grafice a starii plane de tensiuni prin cercul lui Mohr, se poate cu usurinta studia o serie de proprietati ale acesteia. Astfel se poate observa ca tensiunea tangentiala maxima este egala cu raza cercului, deci, cu semidiferenta tensiunilor normale principale. De asemeni, se vede ca aceasta
tensiune corespunde la un unghi de 45o facut cu directiile principale ale tensiunilor normale.
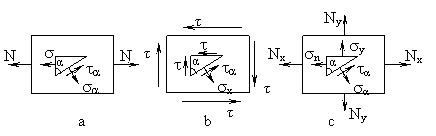
Fig. 5
Starea plana de tensiuni se poate afla intr-o serie de cazuri particulare (fig. 5):
1.Starea liniara de eforturi, cand x 0 si y
Ea se produce in barele drepte intinse sau comprimate (figura 5, a) sau in barele incovoiate.
Pe o sectiune inclinata tensiunile a si ta vor fi in acest caz,
![]()
![]()
relatiile fiind deja cunoscute de la studiul tensiunilor in sectiunea inclinata a unei bare supusa la intindere.
In fig. 6.a, este reprezentat si cercul lui Mohr pentru acest caz.
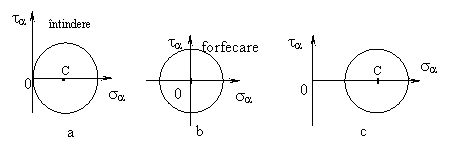
Fig. 6
2. Starea de forfecare pura, atunci cand x y=0. Aceasta se produce in barele solicitate la forfecare pura sau la torsiune. Pe o sectiune oblica, tensiunile sunt,
a txysin2a ta txycos2a
In cazul unghiului de 45o se obtine,
![]()
![]()
iar pe o sectiune perpendiculara pe aceasta (a = 135o),
txy
Rezulta ca pe sectiuni inclinate cu 45 fata de fetele elementului considerat, au loc intinderi si compresiuni pure egale ca marime (fig. 7.a.).
Cercul lui Mohr are in acest caz centrul in originea sistemului de axe (fig. 6.b).
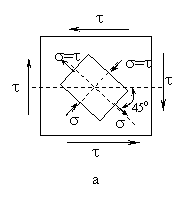
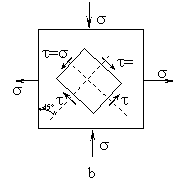
Fig. 7
3. Intindere si compresiune dupa doua directii atunci cand txy = 0. In acest caz x si y sunt tensiuni principale. Aceasta stare se produce in peretele unui rezervor solicitat la presiunea interioara a unui fluid, spre exemplu.
Pentru o sectiune oblica tensiunile a si ta au forma (16). Daca si (fig. 7.b), atunci,
a cos2a ta sin2a
Pentru a si a se obtin,
t
t
aceasta insemnand ca in sectiuni rotite cu 45 fata de fetele elementului se produc forfecari sau lunecari pure. Solicitarea de forfecare pura este deci echivalenta cu intinderea dupa o directie si compresiunea egala pe directie perpendiculara.
In fig. 6.c, este reprezentat cercul lui Mohr pentru acest caz.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |