
UNIVERSITATEA
TEHNICA "GH. ASACHI"
Facultatea Automatizari si Calculatoare
REFERAT PRACTICA
UNIVERSITATEA
TEHNICA "GH. ASACHI"
Facultatea Automatizari si Calculatoare
LUCRARE DE LICENTA
Proiectarea automata a unei structuri secventiale care
sa aiba atasat model de simulator de proces
I. INTRODUCERE
Circuitele materializate cu elemente de comutatie folosesc ca model matematic functiile de variabile binare.Deoarece circuitele realizate cu elemente binare nu pot avea decat doua stari distincte , functiile care descriu aceste circuite vor lua numai doua valori. Aceste functii bivalente de variabile binare se mai numesc si functii booleene sau functii logice si au o deosebita importanta pentru studiul circuitelor logice si al comenzilor secventiale.
Ca urmare, apare necesitatea simplificarii acestor functii logice , fapt ce va duce la reducerea complexitatii circuitelor logice descries de aceste functii , lucru foarte important in sinteza automatelor.
Studiul functiilor booleene se face in multe cazuri pe reprezentarile acestora. Exista o diversitate mare de reprezentari ale functiilor booleene utilizate in mod current.Aceste reprezentari pot fi grupate in doua mari categorii:
-reprezentarile geometrice
-reprezentarile prin coduri
Reprezentarile din prima categorie, fiind intuitive, sunt foarte utile pentru studiul functiilor booleene cu un numar redus de variabile, fara mijloace electronice de calcul. Pentru functii cu numar mare de variabile reprezentarile geometrice se complica foarte mult, devenind practice inutilizabile. Cele mai cunoscute reprezentari geometrice sunt reprezentarile hipercub, prin grafuri si reprezentarile prin digramele Euler, Venn, Veitch si Karnaugh. Existenta acestor reprezentari a permis studiul automatelor cu ajutorul functiilor booleene.
Reprezentarile din a doua categorie, desi sunt mai putin intuitive, au capatat o larga raspandire intrucat permit studiul functiilor cu un numar arbitrar de variabile si utilizarea calculatoarelor electronice. In aceasta categorie se incadreaza atat reprezentarile obisnuite cat si unele reprezentari utile in simplificarea functiilor booleene sau in sinteza automatelor.
II. SIMPLIFICAREA FUNCTIILOR BOOLEENE
Dupa cum se stie , functiile booleene pot fi scrise printr-un numar mare de expresii. Pentru a compara intre ele aceste expresii, din punctual de vedere al complexitatii lor, este necesar sa se stabileasca anumite criterii. In acest scop a fost introdusa notiunea de cost asociata unei expresii date. Pot fi alese functii cost diferite, tinand cont , de exemplu, de costul efectiv al elementelor tehnice pentru realizarea functiei booleene, sau alte criterii. Functiile cost cele mai des utilizate sunt urmatoarele:
C - numarul total de expresii cuprinse in expresie;
C - sumarul total de operatori sau de contacte, cu care se
realizeaza expresia
3. C - numarul total de intrari in schemele cu operatori care realizeaza functiile date.
Trebuie sa atragem atentia ca aceste criterii nu sunt suficiente pentru obtinerea unor reprezentari optimale ale functiilor prin scheme electrice. Spre exemplu, o expresie a unei functii booleene care contine cel mai mic numar de litere poate conduce la scheme cu numar mare de contacte decat o expresie cu un numar mai mare de litere. Numarul de elemente dintr-o reprezentare a functiei depinde nu numai de expresia de la care se pleaca, ci si de metoda de sinteza folosita . Ultimele doua criterii nu sunt potrivite pentru compararea expresiilor unei funtii date , la fel cum primul criteriunu este potrivit pentru compararea intre ele a schemelor care realizeaza functia respectiva , in consecinta , vom folosi primul criteriu pentru aprecierea complexitatii expresiilor si celelalte doua criterii pentru aprecierea complexitatii schemelor.
Operatia de trecere de la o expresie a unei functii booleene la o expreie cu un numar redus de litere se numeste simplificare.Scopul operatiei este de a obtine expresiile cu un numar minim de litere.
Un rol important in operatia de simplificare il joaca determinarea implicantilor primi si a expresiilor care contin numai implicanti primi.
Expresia unei functii booleene care este suma tuturor implicantilor sai primi va fi denumita expresie caracteristica.Oricare alta expresie care contine numai implicanti primi va fi denumita expresie redusa iar expresiile care contin un numar minim de implicanti primi se vor numi expresii minimale.
Metodele de simplificare ale functiilor booleene se pot imparti in doua categorii:
metode tabelare;
metode algebrice.
In categoria metodelor tabelare se incadreaza : metoda diagramei lui
Veitch, metoda diagramei lui Karnaugh si altele.
In continuare ne vom ocupa de metodele algebrice pentru ca sunt programabile pe calculator.
Una din metodele algebrice existente este si metoda simbolica.
Metoda simbolica presupune simplificarea functiilor in doua etape. Intr-o prima etapa se cauta expresia caracteristica, iar in a doua se cauta expresiile minimale, pornind de la expresia gasita in rpima etapa.
Minimizarea functiilor booleene se poate realiza cu ajutorul circuitelor NAND dupa cum urmeaza:
-minimizarea consta in trecerea unei expresii de la forma canonica la o forma elementara;
-regula de minimizare a functiilor scrise sub forma canonica P(forma canonica norma disjunctiva), prin diagrame Karnaugh este urmatoarea:
pentru fiecare termen P se va completa 1 in casuta corespunzatoare combinatiei respective;
se grupeaza grupuri de 1 aflati in patrate adiacente , inclusiv patratele de pe laturile extreme; numarul maxim de casute care contin 1 trebuie sa fie o putere a lui 2;
din fiecare grup se elimina variabilele care isi schimba starea;
se scrie forma minimizata a functiei ca suma a produselor variabilelor ramase din fiecare grup.
Minimizarea functiilor booleene prin metoda simbolica foloseste
reprezentarea functiilor prin symbol de marcare, permitand minimizarea sigura si a functiilor booleene de 10, 12 argumente. Simbolul de marcare este o reprezentare numerica a functiilor si deriva din reprezentarea prin tabel de adevar.
Minimizarea prin metoda simbolica se realizeaza prin intermediul listelor de adiacenta. Daca doi termeni P difera doar prin valoarea binara a unei singure variabile binare, atunci numerele de stae care corespund se numesc adiacente : in octal numerele de adiacenta pot fi 1,2,4,10,20,01,100,200,400 etc.
Primul numar de stare( se considera numerele de stare ordonate crescator in simbol de marcare) va constitui capul primei liste de adiacenta.Lista de adiacenta se formeaza din numerele de stare adiacente cu capul de lista. Pentru a nu fi luat de mai multe ori in formarea listelor de adiacenta , fiecare numar de stare adiacent cu capul de lista se bifeaza in simbolul de marcare prin subliniere.
Primul numar de stare nebifat in simbolul de marcare va fi capul celei de a doua liste de adiacente s.a.m.d pana la cuprinderea tuturor numerelor de stare in liste de adiacente.
In locul in care se treceau numerele de stare in symbol se trece valoarea in binar a capului de lista , fiecare bit fiind trecut in dreptul fiecarui argument. Dispar din componenta implicantului acele argumente care corespund diferentelor de adiacenta marcate in liste. In expresia algebrica a implicantilor esentiali argumentele intra ca atare sau negate dupa cum corespund unui bit 1 sau 0 din desfasurarea capului de lista.
III.Prezentarea limbajului Visual C
Istoria Visual C++
Odata cu acceptarea beneficiilor aduse de interfata grafica a MS Windows (GUI) programarea pentru acest mediu a devenit foarte cautata. Programarea pentru Windows este diferita de cea orientata pe tranzactii (old-style batch). O diferenta esentiala intre cele doua este ca un program rulat sub Windows proceseaza informatiile utilizatorului cu ajutorul mesajelor de la sistemul de operare, pe cand un program MS-DOS foloseste sistemul de operare pentru a furniza informatiile. Visual C++, produs de firma Microsoft, este un limbaj textual ce foloseste un program de construit interfete grafice pentru a usura munca programatorului ce are de construit interfete.
Exista limbaje concepute strict pe baza conceptelor programarii orientate pe obiecte (POO), de exemplu Simula sau Smalltalk. O alta abordare este de a adauga unor limbaje cu o popularitate bine stabilita, de exemplu Pascal si C, elementele tehnicii POO. C++ combina avantajele oferite de limbajul C( eficienta, flexibilitate si popularitate) cu avantajele oferite de tehnica POO. Desi adopta principiile POO, C++ nu impune aplicarea lor stricta ( se pot scrie programe fara elemente POO). Conceptul fundamental in C++ este clasa. Clasele sunt tipuri definite de utilizator, asigura incapsularea datelor, garanteaza initializarea datelor, gestiunea memoriei controlata de utilizator, mecanisme pentru supraincarcarea operatorilor. C++ contine de asemenea imbunatatiri ale limbajului C care nu sunt direct legate de POO, cum ar fi: tipul referinta, substitutia "in-line" a functiilor, nume de functii supraincarcate, operatori pentru gestionarea memoriei libere.
IV.EXEMPLU DE STRUCTURA SECVETIALA
Structura secventiala este prezentata intr-o aplicatie Visual C.Aceasta aplicatie constituie un exemplu de modelare software.
Figura 1. Descrierea procesului
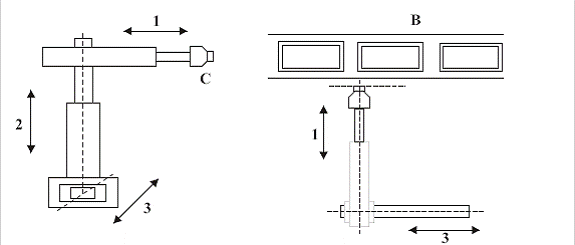
1- Deplasare orizontala brat (avans-retragere);
2- Deplasare verticala corp (ridicare - coborare);
3- Translatie orizontala corp (stanga-dreapta);
C- Cap de vopsire;
B- Banda transportoare.
BIBLIOGRAFIE:
-Corneliu Hutanu-Circuite Logice si
Comenzi numerice, editura Rotaprint,
-A.Pricop,L. Boboc-Analiza si Sinteza Structurilor Logice,editura Tehnica-info , Chisinau,2001;
-A.Pricop-Structuri Logice si
Automatizari Secventiale, editura Rotaprint,
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |