Functii diferentiabile
1. Definitie. Fie ![]() spatii vectoriale
normate finit dimensionale si
spatii vectoriale
normate finit dimensionale si ![]() ,
, ![]() multime
deschisa si
multime
deschisa si ![]() . Functia
. Functia ![]() se numeste diferentiabila in punctul
se numeste diferentiabila in punctul ![]() , daca exista
, daca exista ![]() a.i.
a.i.
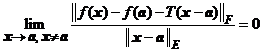 . (1)
. (1)
Aplicatia lineara si continua ![]() , daca exista, este unic determinata, se noteaza cu
, daca exista, este unic determinata, se noteaza cu
![]() . (2)
. (2)
si se citeste " derivata lui ![]() in punctul
in punctul ![]() sau diferentiala
lui
sau diferentiala
lui ![]() in punctul
in punctul ![]() ".
".
2.Lema. Fie ![]() doua spatii vectoriale normate de dimensiune
finita si
doua spatii vectoriale normate de dimensiune
finita si ![]() ,
, ![]() multime
deschisa si functia
multime
deschisa si functia ![]() . Afirmatiile urmatoare sunt echivalente:
. Afirmatiile urmatoare sunt echivalente:
Functia ![]() este diferentiabila
in
este diferentiabila
in ![]() .
.
Exista ![]() si
si ![]()
![]() functie
continua in
functie
continua in ![]() ,
, ![]() a.i. sa aiba
loc relatia
a.i. sa aiba
loc relatia
![]() . (3)
. (3)
Demonstratie. "![]() ". Deoarece
". Deoarece ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() , vom nota cu
, vom nota cu ![]() si definim
functia
si definim
functia
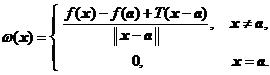 . (4)
. (4)
Este evident ca ![]() este continua in
este continua in ![]() si
si ![]() .
.
"![]() ". trivial.
". trivial.
Egalitatea (3) poate fi scrisa sub urmatoarea forma
![]() . (5)
. (5)
Intr-adevar, din definitia
functiei ![]() deducem ca in
vecinatatea
deducem ca in
vecinatatea ![]() (adica, este
posibil ca pentru orice
(adica, este
posibil ca pentru orice ![]() sa
determinam
sa
determinam ![]() a.i.
a.i. ![]() sa avem
sa avem ![]() ), avem
), avem
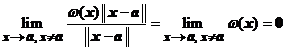 .
.
3. Observatie.
Notam cu ![]() "cresterea functiei
"cresterea functiei ![]() " si cu
" si cu ![]() "cresterea argumentului in jurul punctului
"cresterea argumentului in jurul punctului ![]() ". Atunci relatia (5) se scrie sub forma
". Atunci relatia (5) se scrie sub forma
![]() . (5')
. (5')
Forma
lineara din partea
dreapta a relatiei (5'), care reprezinta aproximarea
lineara a cresterii lui ![]() , se numeste diferentiala
lui
, se numeste diferentiala
lui ![]() in punctul
in punctul ![]() si uneori, se
noteaza cu
si uneori, se
noteaza cu ![]() :
:
![]() (6)
(6)
sau, daca notam cu ![]() , atunci formula (6) se scrie sub forma clasica
, atunci formula (6) se scrie sub forma clasica
![]() (6')
(6')
4. Definitie. Fie ![]() doua spatii vectoriale normate finit dimensionale
si
doua spatii vectoriale normate finit dimensionale
si ![]() ,
, ![]() multime
deschisa. Functia
multime
deschisa. Functia ![]() se numeste diferentiabila pe
se numeste diferentiabila pe ![]() daca este
diferentiabila in orice punct
daca este
diferentiabila in orice punct ![]() si avem
si avem ![]() definita prin
definita prin ![]() si se
citeste "derivata lui
si se
citeste "derivata lui ![]() in punctul
in punctul ![]() ". Deci
". Deci ![]() ,
, ![]() .
.
Functia ![]() daca si
numai daca
daca si
numai daca ![]() este
diferentiabila (derivabila) in orice punct din
este
diferentiabila (derivabila) in orice punct din ![]() si
si ![]() continua pe
continua pe ![]() .
.
5. Observatie.
Daca ![]() este
diferentiabila pe
este
diferentiabila pe ![]() , atunci
, atunci ![]() ia valori in
ia valori in ![]() .
.
Deci ![]() si deoarece
si deoarece ![]() se identifica
izometric cu
se identifica
izometric cu ![]() , atunci putem considera pe
, atunci putem considera pe ![]() ca o functie
definita astfel
ca o functie
definita astfel ![]() .
.
Exercitiul 1.
Fie ![]() doua spatii
vectoriale normate de dimensiune finita,
doua spatii
vectoriale normate de dimensiune finita, ![]() multime
deschisa si functia
multime
deschisa si functia ![]() . Daca
. Daca ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() , atunci
, atunci ![]() este continua in
este continua in ![]() .
.
R. Intr-adevar, daca functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() , atunci exista o intreaga vecinatate
, atunci exista o intreaga vecinatate ![]() , inclusa in
, inclusa in ![]() , a.i. sa se verifica formula (2) oricare ar fi
, a.i. sa se verifica formula (2) oricare ar fi ![]() . Trecand la norma avem
. Trecand la norma avem
![]() ,
,
de unde rezulta continuitatea lui ![]() in punctul
in punctul ![]() .
.
6. Teorema. (Operatii cu functii derivabile).
Fie ![]() ,
, ![]() spatii euclidiene
finit dimensionale (spatii Banach) si
spatii euclidiene
finit dimensionale (spatii Banach) si ![]() , multime deschisa,
, multime deschisa, ![]() si
si ![]() .
.
(1). Daca ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
(2). Daca ![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
(3). Daca ![]() ,
, ![]() functie
lineara atunci
functie
lineara atunci ![]() diferentiabila in orice punct
diferentiabila in orice punct ![]() si avem
si avem ![]() .
.
(4). Daca ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
Demonstratie. Vom observa ca proprietatile
(1) si (2) arata ca derivata este un operator (o aplicatie)
linear, adica ![]() si
si ![]() .
.
(1). Scriem ca ![]() sunt functii
diferentiabile in
sunt functii
diferentiabile in ![]() : exista aplicatiile lineara si continue
: exista aplicatiile lineara si continue ![]() si functiile
si functiile
![]() continue in
continue in ![]() ,
, ![]() a.i.
a.i.
![]() unde
unde ![]() .
.
![]() unde
unde ![]() .
.
Adunand cele doua relatii si
folosind notatiile ![]() ,
, ![]() si
si ![]() , deducem ca functia
, deducem ca functia ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
(2). Din faptul ca ![]() este functie
diferentiabila in
este functie
diferentiabila in ![]() rezulta
existenta aplicatiei lineare si continue
rezulta
existenta aplicatiei lineare si continue ![]() si a
functiei
si a
functiei ![]() continua in
continua in ![]() ,
, ![]() a.i.
a.i.
![]() unde
unde ![]() .
.
Inmultind aceasta relatie cu ![]() , deducem ca
, deducem ca ![]() este
diferentiabila in
este
diferentiabila in ![]() , si are derivata
, si are derivata ![]() .
.
(3). Din faptul ca ![]() este aplicatie
lineara putem scrie
este aplicatie
lineara putem scrie
![]()
si luand ![]() si
si ![]() , rezulta afirmatia din enunt.
, rezulta afirmatia din enunt.
(4). Datorita ipotezei putem scrie
![]() si
si![]() .
.
Daca adunam prima relatie inmultita
cu ![]() cu a doua relatie
inmultita cu
cu a doua relatie
inmultita cu ![]() si vom tine
seama de expresia lui
si vom tine
seama de expresia lui ![]() , obtinem
, obtinem
![]() ,
,
unde
![]() si
si 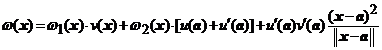 .
.
Relatia obtinuta
arata ca ![]() este
diferentiabila in
este
diferentiabila in ![]() (
(![]() aplicatie lineara si
aplicatie lineara si ![]() este vector fixat iar
este vector fixat iar ![]() aplicatie
lineara si
aplicatie
lineara si ![]() vector fixat.
vector fixat.
7. Observatie. Orice functie ![]() diferentiabila in
diferentiabila in ![]() , unde
, unde ![]() si
si ![]() sunt spatii
vectoriale finit dimensionale, este continua in
sunt spatii
vectoriale finit dimensionale, este continua in ![]() .
.
8. Teorema. (Diferetiala functiilor compuse).
Fie ![]() ,
, ![]() si
si ![]() spatii euclidiene (spatii Banach) si
multimile deschise
spatii euclidiene (spatii Banach) si
multimile deschise ![]() ,
, ![]() ,
, ![]() ,
, ![]() si
si ![]() . Daca functia
. Daca functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() este
diferentiabila in
este
diferentiabila in ![]() , atunci functia compusa
, atunci functia compusa ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem
![]() .
.
Demonstratie. Conform ipotezei, functiei compuse ![]() ,
, ![]() ii asociem
aplicatia lineara
ii asociem
aplicatia lineara ![]() ,
, ![]() .
.
Interpretam faptul ca ![]() este
diferentiabila in
este
diferentiabila in ![]() : exista
aplicatia lineara si continua
: exista
aplicatia lineara si continua ![]() si functia
si functia ![]() continua in
continua in ![]() ,
, ![]() a.i.
a.i.
![]() unde
unde ![]() .
. ![]()
Interpretam faptul ca ![]() este
diferentiabila in
este
diferentiabila in ![]() : exista
aplicatia lineara si continua
: exista
aplicatia lineara si continua ![]() si functia
si functia ![]() continua in
continua in ![]() ,
, ![]() a.i.
a.i.
![]() unde
unde ![]() .
. ![]()
Deoarece pentru orice ![]() avem
avem ![]() , inlocuind in relatia
, inlocuind in relatia ![]() valorile
valorile ![]() si
si ![]() obtinem
obtinem
![]() .
.
Daca notam ![]() si folosim
si folosim ![]() atunci putem scrie
atunci putem scrie
![]() ,
,
sau, pentru orice ![]() avem
avem
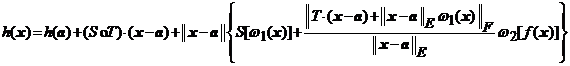 ,
,
unde ![]() . Avem
. Avem
![]() ,
, ![]()
si 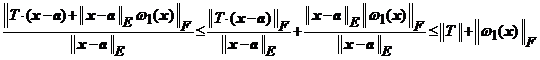 ,
,
De aici deducem ca in relatia de mai sus ultima
paranteza tinde la zero, cand ![]() si deci,
si deci,
![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() .
.
Derivate partiale
Vom considera cazurile particulare cand ![]() si
si ![]() .
.
Definitie. Fie ![]() o multime
deschisa si functia
o multime
deschisa si functia ![]() ,
, ![]() si fie punctul
si fie punctul ![]() . Daca exista
si este finita limita
. Daca exista
si este finita limita
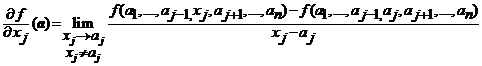 , (7)
, (7)
atunci aplicatia![]() se numeste derivata
partiala a lui
se numeste derivata
partiala a lui ![]() in raport cu
in raport cu ![]() , calculata in
punctul
, calculata in
punctul ![]() .
.
Uneori, derivata partiala ![]() se va nota cu
se va nota cu ![]() sau cu
sau cu ![]() .
.
Spunem ca functia ![]() are derivata
partiala in raport cu
are derivata
partiala in raport cu ![]() in
in ![]() daca este
derivabila partial in raport cu
daca este
derivabila partial in raport cu ![]() in orice punct din
in orice punct din ![]() .
.
Daca ![]() admite derivate
partiale in raport cu
admite derivate
partiale in raport cu ![]() in orice punct
in orice punct ![]() , atunci functia care in fiecare punct
, atunci functia care in fiecare punct ![]() are valoarea
are valoarea ![]() se va nota cu
se va nota cu ![]() si se
numeste derivata partiala
a lui
si se
numeste derivata partiala
a lui ![]() in raport cu variabila
in raport cu variabila
![]() . Daca
. Daca ![]() este derivabila
in raport cu variabila
este derivabila
in raport cu variabila ![]() in orice punct din
in orice punct din ![]() , atunci notam cu
, atunci notam cu
![]() sau
sau 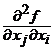 , pentru orice
, pentru orice ![]() , (8)
, (8)
derivatele partiale de
ordinul al doilea ale ![]() in raport cu
variabilele
in raport cu
variabilele ![]() si
si ![]() .
.
In cazul particular, cand ![]() si
si ![]() , notatia din formula (2) este interpretata ca in urmatoarea
, notatia din formula (2) este interpretata ca in urmatoarea
10.
Teorema. Fie ![]() ,
, ![]() multime
deschisa,
multime
deschisa, ![]() si
si ![]() . Daca functia
. Daca functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() atunci:
atunci:
exista toate derivatele
partiale ![]() ;
;
(2). ![]() ;
;
(3). ![]() ,
, ![]() ;
;
(4). ![]() ,
,
unde s-a notat ![]() .
.
11.
Teorema (Criteriul lui Schwarz). Fie ![]() ,
, ![]() ,
, ![]() multime
deschisa. Daca se verifica conditiile:
multime
deschisa. Daca se verifica conditiile:
(1).
Functia ![]() admite derivate
partiale mixte de ordinul al doilea
admite derivate
partiale mixte de ordinul al doilea ![]() si
si ![]() intr-o vecinatate
intr-o vecinatate
![]() ;
;
(2).
Derivatele ![]() si
si ![]() sunt functii
continue in punctul
sunt functii
continue in punctul ![]() .
.
Atunci are loc egalitatea ![]() .
.
Demonstratie. Fie punctul ![]() , oarecare, dar fixat, a.i.
, oarecare, dar fixat, a.i. ![]() . Definim expresia
. Definim expresia
![]() .
.
Fara a restrange generalitatea, putem presupune ![]() . Definim functia
. Definim functia ![]() , prin relatia
, prin relatia
![]() .
.
Atunci, functia ![]() este derivabila pe intervalul
este derivabila pe intervalul ![]() si au loc
relatiile:
si au loc
relatiile:
![]() si
si ![]() .
.
Asadar, functia ![]() satisface teorema lui
Lagrange pe intervalul
satisface teorema lui
Lagrange pe intervalul ![]() si deci,
exista
si deci,
exista ![]() a.i. sa avem
a.i. sa avem ![]() . Folosind relatiile de mai sus, deducem ca
. Folosind relatiile de mai sus, deducem ca ![]() se poate scrie sub
forma
se poate scrie sub
forma
![]() . (9)
. (9)
Fie acum ![]() si functia
si functia ![]() , definita prin
, definita prin 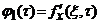 . Deoarece
. Deoarece ![]() exista in
exista in ![]() , rezulta ca functia
, rezulta ca functia ![]() este derivabila
pe
este derivabila
pe ![]() si avem
si avem ![]() .
.
Aplicand teorema lui Lagrange pe intervalul ![]() atunci exista
atunci exista ![]() a.i. sa avem
a.i. sa avem
![]() . (10)
. (10)
Comparand ultima relatie (10) cu relatia (9), deducem
![]() . (11)
. (11)
Analog, cu ajutorul functiei ![]() , deducem ca exista
, deducem ca exista ![]() a.i.
a.i.
![]() . (12)
. (12)
Fie functia ![]() . Procedand ca mai sus, rezulta ca exista
. Procedand ca mai sus, rezulta ca exista ![]() a.i.
a.i.
![]() . (13)
. (13)
Din (11) si (13) deducem egalitatea
![]() unde
unde ![]() si
si ![]() . (14)
. (14)
Din modul cum s-a construit egalitatea (14),
rezulta ca pentru fiecare punct ![]() exista doua
numere
exista doua
numere ![]() si
si ![]() cuprinse intre
cuprinse intre ![]() si
si ![]() si doua
numere
si doua
numere ![]() si
si ![]() cuprinse intre
cuprinse intre ![]() si
si ![]() a.i.
a.i.
![]() .
.
Folosind continuitatea prin siruri a
functiilor ![]() si
si ![]() in punctul
in punctul ![]() , daca
, daca ![]() si
si ![]() , cand
, cand ![]() , deducem egalitatea derivatelor mixte de ordinul al doilea
in
, deducem egalitatea derivatelor mixte de ordinul al doilea
in ![]() .
.
12. Observatie.
Daca derivatele partiale mixte de ordinul al doilea ![]() si
si ![]() exista si
sunt continue pe
exista si
sunt continue pe ![]() atunci ele sunt egale
pe
atunci ele sunt egale
pe ![]() , adica
, adica ![]() .
.
In cazul mai general, cand ![]() , putem enunta
, putem enunta
13.
Criteriul lui Schwarz.. Fie ![]() ,
, ![]() multime
deschisa si
multime
deschisa si ![]() . Daca se verifica conditiile:
. Daca se verifica conditiile:
1). Functia ![]() admite derivate partiale mixte de ordinul al
doilea
admite derivate partiale mixte de ordinul al
doilea ![]() si
si ![]() intr-o vecinatate
intr-o vecinatate
![]() ;
;
2). Derivatele ![]() si
si ![]() sunt functii
continue in punctul
sunt functii
continue in punctul ![]() .
.
Atunci are loc egalitatea
![]() si
si ![]() .
.
14. Observatie.
O teorema asemanatoare criteriului lui Schwarz ramane valabila si pentru
derivatele partiale de ordin superior; daca mai multe derivate
partiale mixte, in care variabilele in raport cu care se efectueaza
derivarea intervin de acelasi numar de ori, exista si sunt
continue pe ![]() atunci ele sunt egale
pe
atunci ele sunt egale
pe ![]() .
.
De exemplu, daca derivatele
partiale mixte de ordinul al treilea ![]() si
si ![]() exista si
sunt continue pe
exista si
sunt continue pe ![]() atunci are loc
egalitatea
atunci are loc
egalitatea
![]() .
.
15.
Teorema.(Criteriul lui Young). Fie ![]() ,
, ![]() multime
deschisa si
multime
deschisa si ![]() . Daca exista derivatele partiale
. Daca exista derivatele partiale ![]()
![]() si acestea sunt
functii diferentiabile in
si acestea sunt
functii diferentiabile in ![]() , atunci exista toate derivatele partiale de
ordinul al doilea in
, atunci exista toate derivatele partiale de
ordinul al doilea in ![]() , iar derivatele partiale mixte sunt egale
, iar derivatele partiale mixte sunt egale ![]() ,
,
![]() si
si ![]() .
.
Diferentiala functiilor compuse de doua variabile
Vom analiza cazul functiilor de
doua variabile. Fie ![]() si
si ![]() doua multimi
deschise din plan si functiile
doua multimi
deschise din plan si functiile ![]() ,
, ![]() si
si ![]() ,
, ![]() . Fie functia reala
. Fie functia reala ![]() ,
, ![]() . Atunci, putem considera functia compusa
. Atunci, putem considera functia compusa
![]() ,
,
definita pentru orice ![]() , cu valori reale.
, cu valori reale.
Figura 1. Compunerea functiilor de doua variabile.
16.
Propozitie. Daca
functiile ![]() si
si ![]() ,
, ![]() sunt
diferentiabile pe
sunt
diferentiabile pe ![]() , iar functia
, iar functia ![]() este
diferentiabila pe
este
diferentiabila pe ![]() , atunci functia compusa
, atunci functia compusa ![]() este
diferentiabila pe
este
diferentiabila pe ![]() si avem
si avem
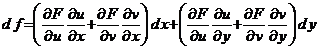 . (15)
. (15)
Demonstratie. Intr-adevar, din formula diferentialei putem scrie
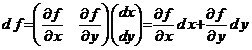
si daca
inlocuim derivatele partiale ![]() si
si ![]() cu expresiile
cu expresiile
![]()
![]() ,
,
atunci se obtine relatia cautata.
17. Observatie.
Diferentialele functiilor ![]() si
si ![]() conserva forma prin
operatia de compunere a functiilor, in schimb, existenta
derivatelor partiale ale acestor functii poate sa nu fie
conservata prin aceasta operatie.
conserva forma prin
operatia de compunere a functiilor, in schimb, existenta
derivatelor partiale ale acestor functii poate sa nu fie
conservata prin aceasta operatie.
De exemplu, fie functiile
![]()
si functia
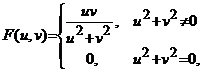
![]() .
.
Alegem ![]() si punctul
corespunzator
si punctul
corespunzator ![]() . Functiile
. Functiile ![]() si
si ![]() sunt
difrentiabile pe
sunt
difrentiabile pe ![]() si deci in punctul
si deci in punctul
![]() , iar functia
, iar functia ![]() are derivate
partiale in
are derivate
partiale in ![]() (dar nu este
diferentiabila in acest punct):
(dar nu este
diferentiabila in acest punct):
![]() .
.
Functia compusa ![]() , definita prin expresia
, definita prin expresia
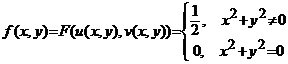 pentru
pentru ![]() ,
,
nu are derivate partiale in origine, deoarece functia
![]() , nu are limita cand
, nu are limita cand ![]() .
.
Analog, functia ![]() , nu are limita cand
, nu are limita cand ![]() .
.
Asadar, functia compusa ![]() nu are derivate
partiale in
nu are derivate
partiale in ![]() .
.
Pentru a arata ca
diferentialele functiilor ![]() si
si ![]() au aceeasi
forma, sa desfacem parantezele in formula (15), dand factor comun pe
au aceeasi
forma, sa desfacem parantezele in formula (15), dand factor comun pe ![]() si
si ![]() . Avem
. Avem
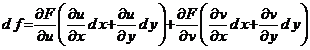 . (16)
. (16)
si deoarece avem
![]() si
si![]() ,
,
rezulta ca
![]() se scrie formal cu
ajutorul relatiei
se scrie formal cu
ajutorul relatiei
![]() . (17)
. (17)
Pe de alta parte avem
![]() . (18)
. (18)
Comparand relatiile (17) si (18)
deducem ca diferentiabilele functiilor ![]() si
si ![]() au aceeasi
forma si aceasta constitue invarianta
diferentialei intai fata
de operatia de compunere a functiilor.
au aceeasi
forma si aceasta constitue invarianta
diferentialei intai fata
de operatia de compunere a functiilor.
Desigur, aceasta invarianta a diferentialei este formala (comparativ cu invarianta diferentiabilitatii fata de compunerea functiilor).
Intr-adevar, relatia (17) se scrie
![]() ,
,
de unde, observam ca in
aceasta formula ![]() si
si ![]() sunt in fapt diferentialele functiilor
sunt in fapt diferentialele functiilor ![]() si
si ![]() , definite pentru orice
, definite pentru orice ![]() . Pe de alta parte, relatia (18) se scrie complet
prin formula
. Pe de alta parte, relatia (18) se scrie complet
prin formula
![]() ,
,
in care ![]() si
si ![]() sunt
diferentialele variabilelor
sunt
diferentialele variabilelor ![]() .
.
O alta proprietate de invarianta prin operatia de compunere a functiilor este existenta si continuitatea derivatelor partiale. Acest rezultat este dat de urmatoarea
18.
Propozitie. Daca
functiile ![]() si
si ![]() , au derivate partiale continue in orice
, au derivate partiale continue in orice ![]() , iar functia
, iar functia ![]() are derivate
partiale continue pe
are derivate
partiale continue pe ![]() , atunci functia compusa
, atunci functia compusa
![]() ,
,
are derivate partiale
continue pe ![]() .
.
Demonstratie. Deoarece functiile ![]() ,
, ![]() si
si ![]() au derivate
partiale continue, atunci aceste functii sunt diferentiabile
(si implicit continue). Asadar, functia compusa este
diferentiabila si are derivatele partiale definite de
formulele:
au derivate
partiale continue, atunci aceste functii sunt diferentiabile
(si implicit continue). Asadar, functia compusa este
diferentiabila si are derivatele partiale definite de
formulele:
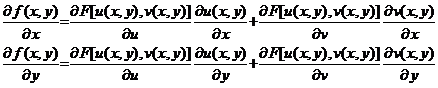 ; (19)
; (19)
Functiile care apar in
membrul drept al acestor relatii sunt continue, prin ipoteza, cum
sunt derivatele partiale ale functiilor ![]() si
si ![]() sau reprezentand
compunere de functii continue. Deci, derivatele partiale
sau reprezentand
compunere de functii continue. Deci, derivatele partiale ![]() si
si ![]() sunt functii
continue pe
sunt functii
continue pe ![]() .
.
Exercitiul 2. Aratati ca functia ![]() , unde
, unde ![]() este de clasa
este de clasa ![]() pe un anumit domeniu
pe un anumit domeniu ![]() , verifica ecuatia diferentiala
, verifica ecuatia diferentiala 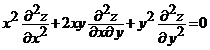 .
.
Indicatie. Consideram functia ![]() si functia
compusa
si functia
compusa ![]() . Atunci
. Atunci
![]() .
.
Calculam derivatele
partiale ale functiei ![]() . Avem
. Avem
![]() ;
;
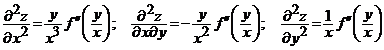 .
.
Exercitiul 3. Aratati ca fiecare din
functiile ![]() , respectiv
, respectiv ![]() , unde
, unde ![]() este de clasa
este de clasa ![]() pe un anumit domeniu
pe un anumit domeniu ![]() , verifica ecuatia diferentiala
, verifica ecuatia diferentiala
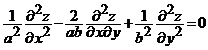 .
.
Solutie. Derivam functia ca produs dintre
functiile ![]() respectiv
respectiv ![]() si functia
compusa
si functia
compusa ![]() , unde
, unde ![]() : in primul caz, avem
: in primul caz, avem
![]() ;
;
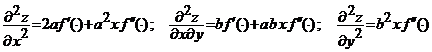 .
.
1 Definitie. Fie ![]() si
si ![]() doua spatii
vectoriale finit dimensionale si
doua spatii
vectoriale finit dimensionale si ![]() o multime
deschisa si
o multime
deschisa si ![]() . Functia
. Functia ![]() este de doua ori diferentiabila in
punctul
este de doua ori diferentiabila in
punctul ![]() daca sunt
verificate conditiile:
daca sunt
verificate conditiile:
(1). functia ![]() este
diferentiabila pe o vecinatate deschisa
este
diferentiabila pe o vecinatate deschisa ![]() ,
, ![]() .
.
(2). aplicatia derivata ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
In aceste conditii, avem ![]() si se va numi derivata a doua a lui
si se va numi derivata a doua a lui ![]() in
in ![]() (se mai foloseste
notatia
(se mai foloseste
notatia ![]() ) si avem
) si avem ![]() , adica
, adica ![]() este aplicatie
bilineara:
este aplicatie
bilineara: ![]() .
.
Functia ![]() este de doua ori diferentiabila pe
este de doua ori diferentiabila pe ![]() daca este de doua
ori diferentiabila in
orice punct
daca este de doua
ori diferentiabila in
orice punct ![]() .
.
Are loc diagrama:
|
|
|
|
|
![]()
![]()
![]()
|
derivatele partiale de ordinul doi exista in |
|
|
|
|
|
|
![]()
|
|
20. Propozitie.
Daca functiile ![]() si
si ![]() ,
, ![]() sunt
diferentiabile de doua ori intr-o vecinatate a punctul
sunt
diferentiabile de doua ori intr-o vecinatate a punctul ![]() , iar functia
, iar functia ![]() este de doua ori diferentiabila
intr-o vecinatate a punctului
corespunzator
este de doua ori diferentiabila
intr-o vecinatate a punctului
corespunzator ![]() , atunci functia compusa
, atunci functia compusa
![]()
este diferentiabila de doua ori in punctul ![]() si avem
si avem
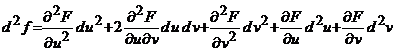 , (20)
, (20)
unde derivatele partiale ale functiei ![]() sunt calculate in
sunt calculate in ![]() , iar diferentialele functiilor
, iar diferentialele functiilor ![]() si
si ![]() sunt calculate in
punctul
sunt calculate in
punctul ![]() .
.
Demonsteratie. Deoarece functiile ![]() si
si ![]() sunt
diferentiabile de doua ori intr-o vecinatate
sunt
diferentiabile de doua ori intr-o vecinatate ![]() , atunci exista
, atunci exista ![]() si
si ![]() si acestea sunt
diferentiabile in
si acestea sunt
diferentiabile in ![]() . Functia compusa are derivate partiale de
ordinul intai si au loc relatiile (19). In membrul drept al
relatiilor (19) apar numai functii diferentiabile. Atunci,
functiile compuse
. Functia compusa are derivate partiale de
ordinul intai si au loc relatiile (19). In membrul drept al
relatiilor (19) apar numai functii diferentiabile. Atunci,
functiile compuse
![]() si
si ![]() ,
,
sunt diferentiabile in ![]() si deci
functiile
si deci
functiile ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() , ceea ce arata ca functia compusa
, ceea ce arata ca functia compusa ![]() este de doua ori diferentiabila in
este de doua ori diferentiabila in ![]() . Asadar, functia compusa
. Asadar, functia compusa ![]() are toate derivatele partiale
de ordinul al doilea si, potrivit criteriului lui Young, derivatele
partiale mixte sunt egale in
are toate derivatele partiale
de ordinul al doilea si, potrivit criteriului lui Young, derivatele
partiale mixte sunt egale in ![]() .
.
Atunci, putem scrie
![]() .
.
Folosind relatiile:
![]() si
si ![]() ;
;
![]() ;
;
![]() ,
,
deducem relatia (20).
21. Observatie. Formula (20) se scrie, formal, cu ajutorul operatorului de derivare astfel:
![]() . (21)
. (21)
22. Observatie. Deoarece ![]() este
diferentiabila de doua ori intr-o vecinatate
este
diferentiabila de doua ori intr-o vecinatate ![]() a punctului
corespunzator
a punctului
corespunzator ![]() , ea are derivatele partiale
, ea are derivatele partiale ![]() si
si ![]() diferentiabile pe
diferentiabile pe
![]() . Daca functia este diferentiabila de
doua ori numai in
. Daca functia este diferentiabila de
doua ori numai in ![]() , atunci deducem ca functia compusa are
derivate partiale de ordinul intai numai in
, atunci deducem ca functia compusa are
derivate partiale de ordinul intai numai in ![]() , deci
, deci ![]() nu este de doua
ori diferentiabila.
nu este de doua
ori diferentiabila.
23. Observatie. Formula diferentialei de ordinul al doilea a functiei compuse se poate obtine din egalitatea
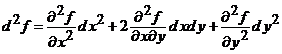 , (22)
, (22)
in care substituim formulele derivatelor partiale de ordinul al doilea ale functiei compuse, definite prin:
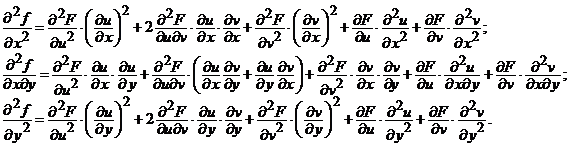 (23)
(23)
24.
Observatie. Comparand formula (20)
cu diferentiala de ordinul al doilea al functiei ![]() ,
,
![]() , (24)
, (24)
observam
ca ![]() si
si ![]() difera prin
termenul
difera prin
termenul 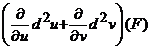 ; astfel, putem vorbi de noninvarianta
diferentialei de ordinul al doilea.
; astfel, putem vorbi de noninvarianta
diferentialei de ordinul al doilea.
Matricea lui Jacobi[1]. Derivatele partiale pentru functii compuse.
25.
Definitie. Fie ![]() si
si ![]()
![]() o multime
deschisa,
o multime
deschisa, ![]() si functia
si functia ![]() ,
, ![]() , despre care presupunem ca este diferentiabila
in
, despre care presupunem ca este diferentiabila
in ![]() . Notam cu
. Notam cu ![]() aplicatia
lineara si continua
aplicatia
lineara si continua ![]() (retinem ca
(retinem ca ![]() este bine definit,
intrucat
este bine definit,
intrucat ![]() poate fi definit in
orice punct din
poate fi definit in
orice punct din ![]() ). Matricea asociata lui
). Matricea asociata lui ![]() (relativ la bazele
canonice din
(relativ la bazele
canonice din ![]() si
si ![]() ) se numeste matricea
Jacobi (matricea jacobiana)
asociata functiei
) se numeste matricea
Jacobi (matricea jacobiana)
asociata functiei ![]() in punctul
in punctul ![]() sau diferentiala lui
sau diferentiala lui ![]() in punctul
in punctul ![]() si se
noteaza cu
si se
noteaza cu ![]() , sau cu
, sau cu
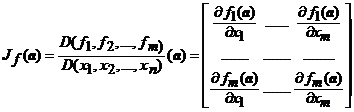 . (25)
. (25)
26. Observatie.
A determina aplicatia lineara si continua ![]() revine la calculul
matricei jacobiene
revine la calculul
matricei jacobiene ![]() relativ la bazele
canonice din
relativ la bazele
canonice din ![]() si
si ![]() .
.
Fie vectorul
![]() . Atunci, ca mai inainte, notam cu
. Atunci, ca mai inainte, notam cu 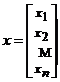 , matricea coloana care contine componentele lui
, matricea coloana care contine componentele lui ![]() . Din definitia matricei jacobiene rezulta ca
putem scrie
. Din definitia matricei jacobiene rezulta ca
putem scrie
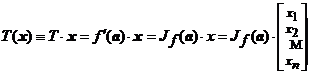 . (26)
. (26)
27.
Corolar. Fie ![]() si
si ![]() multimi deschise,
multimi deschise,
![]() ,
, ![]() si punctul
si punctul ![]() . Consideram functiile
. Consideram functiile ![]() . Daca functia
. Daca functia ![]() este diferentiabila
in punctul
este diferentiabila
in punctul ![]() si functia
si functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() , atunci functia compusa
, atunci functia compusa ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem
![]() . (27)
. (27)
Demonstratie. Vom observa ca aplicatiile
lineare ![]() si
si ![]() exista si
are loc compunerea
exista si
are loc compunerea ![]() . Functia
. Functia ![]() este o aplicatie
lineara si continua. Atunci, matricea jacobiana
asociata functiei
este o aplicatie
lineara si continua. Atunci, matricea jacobiana
asociata functiei ![]() in punctul
in punctul ![]() , notata
, notata ![]() , este egala cu produsul matricelor
, este egala cu produsul matricelor ![]() si
si ![]() .
.
28.
Propozitie. Fie ![]() ,
, ![]() multime
deschisa,
multime
deschisa, ![]() si
si ![]() . Notam cu
. Notam cu ![]() si
si ![]() ,
, ![]() . Atunci proprietatile urmatoare sunt
echivalente:
. Atunci proprietatile urmatoare sunt
echivalente:
functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() (respectiv
(respectiv ![]() );
);
functiile
coordonate ![]() sunt diferentiabile
in
sunt diferentiabile
in ![]() (respectiv
(respectiv ![]() ).
).
2 Corolar. (Derivatele partiale pentru functii
compuse). Fie multimile deschise ![]() si
si ![]() si compunerea
functiilor
si compunerea
functiilor ![]() . Daca
. Daca ![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() este
diferentiabila in
este
diferentiabila in ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem
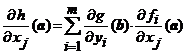 ,
,![]() , (28)
, (28)
unde ![]() si
si ![]() .
.
Demonstratie. In formula (28) derivatele partiale
sunt considerate ca numere si deci in locul aplicatiei lineare ![]() luam
luam ![]() si atunci in (28)
derivatele partiale se inmultesc. Sa observam ca din
modul cum sunt definite functiile
si atunci in (28)
derivatele partiale se inmultesc. Sa observam ca din
modul cum sunt definite functiile ![]() si
si ![]() , ele au cate o singura componenta si deci
matricile jacobiene asociate au o singura linie. Scriind dezvoltat
relatia
, ele au cate o singura componenta si deci
matricile jacobiene asociate au o singura linie. Scriind dezvoltat
relatia ![]() avem
avem
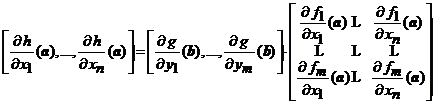 , (29)
, (29)
de unde, se deduce relatia (8).
30. Observatie.
Fie ![]() . Daca exista derivatele partiale
. Daca exista derivatele partiale ![]() si
si ![]() intr-un punct, nu
rezulta ca
intr-un punct, nu
rezulta ca ![]() este continua
si diferentiabila in acel punct. Dar daca aceste derivate
partiale exista si sunt continue intr-o vecinatate a
punctului repectiv, atunci
este continua
si diferentiabila in acel punct. Dar daca aceste derivate
partiale exista si sunt continue intr-o vecinatate a
punctului repectiv, atunci ![]() este
diferentiabila in acel punct.
este
diferentiabila in acel punct.
De exemplu, functia ![]() ,
, 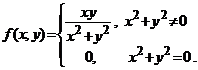 nu este continua
in origine si in consecinta, nu este diferentiabila in origine, desi are derivatele partiale egale cu zero
in origine.
nu este continua
in origine si in consecinta, nu este diferentiabila in origine, desi are derivatele partiale egale cu zero
in origine.
Exercitiul
4. Fie functia ![]() , unde
, unde ![]() , definita prin
, definita prin
![]() .
.
(1). Scrieti functiile coordonate
ale lui ![]() . (R.
. (R. ![]() ).
).
(2). Determinati derivatele partiale de ordinul intai ale functiilor coordonate.
R.
![]()
![]() .
.
(3). Scrieti matricea
lui Jacobi asociata functiei ![]() in punctul
in punctul ![]() .
.
R. 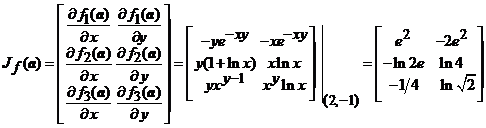 .
.
Exercitiul
5. Fie functia ![]() , definita prin formula
, definita prin formula ![]() ,
, ![]() si functia
si functia ![]() , definita prin
, definita prin ![]() .
.
(1). Determinati functia
compusa ![]() ,
, ![]() .
.
(2). Aratati ca functia
compusa ![]() este
diferentiabila in
este
diferentiabila in ![]() ; calculati
; calculati ![]() .
.
Solutie.(1). Fie ![]() si
si ![]() functiile coordonate ale lui
functiile coordonate ale lui ![]() .
.
Atunci, punand ![]() si
si ![]() obtinem
functia compusa
obtinem
functia compusa ![]() . Deci, putem scrie,
. Deci, putem scrie,
![]() , oricare ar fi
, oricare ar fi ![]() .
.
(2). Functia
![]() este
diferentiabila in orice punct
este
diferentiabila in orice punct ![]() (
(![]() este functie elementara). In particular, functia
este functie elementara). In particular, functia
![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() si, dupa un
calcul simplu, obtinem
si, dupa un
calcul simplu, obtinem
![]() ,
,
unde ![]() .
.
Altfel. Observam ca functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() si functia
si functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() si, potrivit
corolarului 1, avem
si, potrivit
corolarului 1, avem
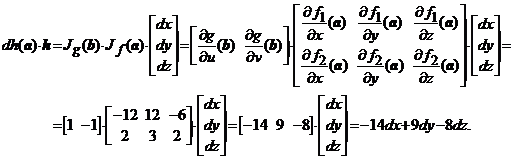
Functii omogene. Teorema lui Euler pentru functii omogene. Teorema lui Lagrange.
31.
Definitie. Multimea
![]() se numeste con deschis in
se numeste con deschis in ![]() avand varful in
originea
avand varful in
originea ![]() daca si
numai daca
daca si
numai daca ![]() , atunci si
, atunci si ![]() , pentru orice
, pentru orice ![]() .
.
Din definitie, observam ca
multimea ![]() este un con avand varful in originea
este un con avand varful in originea ![]() , daca odata cu orice punct
, daca odata cu orice punct ![]() din multimea
din multimea ![]() atunci intreaga
semidreapta care uneste punctul
atunci intreaga
semidreapta care uneste punctul ![]() cu originea
cu originea ![]() este
continuta in
este
continuta in ![]() .
.
Fie ![]() un con deschis cu varful in
un con deschis cu varful in ![]() . Functia
. Functia ![]() se numeste omogena de grad
se numeste omogena de grad ![]() , daca si numai daca
, daca si numai daca
![]() ,
, ![]() si
si ![]() . (30)
. (30)
sau echivalent,
![]() ,
, ![]() si
si ![]() .
.
32. Observatie.
Functia omogena este definita in tot conul ![]() cu exceptia varfului
conului.
cu exceptia varfului
conului.
Exemple:1).Functia ![]() , unde
, unde ![]() , este omogena de gradul
, este omogena de gradul ![]() .
.
2). Functia ![]() si
si ![]() , este omogena de grad
, este omogena de grad ![]() .
.
3). Functia 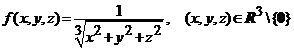 , este omogena de grad
, este omogena de grad ![]() .
.
33.
Teorema (Teorema lui Euler pentru functii
omogene). Fie ![]() un con deschis cu varful in
un con deschis cu varful in ![]() . Daca functia
. Daca functia ![]() este omogena de grad
este omogena de grad ![]() si
diferentiabila in punctul
si
diferentiabila in punctul ![]() (evident
(evident ![]() ) atunci are loc relatia
) atunci are loc relatia
![]() . (31)
. (31)
Demonstratie. Fie functia ![]() , definita prin
, definita prin ![]() . Atunci
. Atunci ![]() este derivabila
pe
este derivabila
pe ![]() si folosind formula de derivare a functiilor
compuse avem
si folosind formula de derivare a functiilor
compuse avem
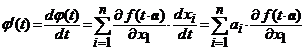 ,
, ![]() .
.
Alegand ![]() , obtinem
, obtinem 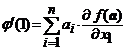 . Pe de alta
parte, daca tinem seama ca
. Pe de alta
parte, daca tinem seama ca ![]() este omogena de
grad
este omogena de
grad ![]() , prin derivarea functiei
, prin derivarea functiei ![]() obtinem:
obtinem:
![]() .
.
Daca functia ![]() este omogena de grad
este omogena de grad ![]() si diferentiabila in orice punct
si diferentiabila in orice punct ![]() ,
, ![]() , atunci are loc relatia
, atunci are loc relatia
![]() . (32)
. (32)
Relatia (32) ne permite sa demonstram urmatoarea
34. Teorema (Reciproca teoremei lui Euler).
Fie ![]() un con deschis cu varful in
un con deschis cu varful in ![]() . Daca functia
. Daca functia ![]() este diferentiabila
in orice punct
este diferentiabila
in orice punct ![]() ,
, ![]() si verifica (32),
si verifica (32),
![]() ,
,
atunci ![]() este o functie omogena
de grad
este o functie omogena
de grad ![]() pe
pe ![]() .
.
Demonstratie. Fie ![]() , un punct oarecare din conul
, un punct oarecare din conul ![]() . Atunci
. Atunci ![]() si functia
si functia ![]() , definita prin
, definita prin ![]() ,
, ![]() este derivabila
pentru orice
este derivabila
pentru orice ![]() . Avem
. Avem
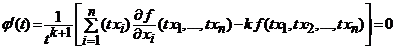 ,
, ![]() ,
,
deci ![]() este
este ![]() . Asadar,
. Asadar, ![]() , adica
, adica
![]() ,
, ![]() ,
,
care arata ca ![]() este omogena pe
este omogena pe ![]() .
.
35.
Teorema cresterilor finite.
Fie ![]() si functia
si functia ![]() . Daca
. Daca ![]() este continua pe
este continua pe ![]() si
diferentiabila pe
si
diferentiabila pe ![]() , atunci exista
, atunci exista ![]() astfel incat
astfel incat
![]() . (33)
. (33)
Demonstratie. Fie ![]() ,
, ![]() , unde functii reale de variabila reala
definite prin
, unde functii reale de variabila reala
definite prin ![]() , sunt functiile coordonate ale lui
, sunt functiile coordonate ale lui ![]() . Din ipoteza deducem ca aceste functii sunt
continue pe
. Din ipoteza deducem ca aceste functii sunt
continue pe ![]() si derivabile pe
si derivabile pe ![]() . In consecinta, functia
. In consecinta, functia ![]() , definita prin
, definita prin
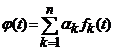 ,
, ![]() , unde
, unde ![]() ,
,
satisface conditiile teoremei lui
Lagrange pe ![]() . Asadar, exista
. Asadar, exista ![]() a.i.
a.i. ![]()
Pe de alta parte, avem: 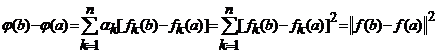 si
si
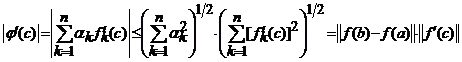 .
.
Inlocuind aceste relatii in formula lui Lagrange, dupa
simplificarea cu ![]() , obtinem (33).
, obtinem (33).
36.
Lema. Fie ![]() un interval deschis,
un interval deschis,![]() un spatiu vectorial normat,
un spatiu vectorial normat,![]() ,
, ![]() diferentiabila in
diferentiabila in ![]() si
si ![]() . Atunci
. Atunci
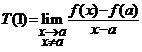 .
.
Demonstratie. Din definitia diferentialei, avem
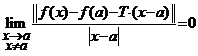 . Deoarece
. Deoarece ![]() atunci
atunci ![]() si deci,
si deci, 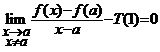 .
.
37.
Teorema cresterilor finite.
Fie ![]() , un interval inchis al axei reale,
, un interval inchis al axei reale, ![]() un spatiu
vectorial normat si functiile
un spatiu
vectorial normat si functiile ![]() si
si ![]() . Presupunem ca sunt verificate conditiile:
. Presupunem ca sunt verificate conditiile:
(1). functiile ![]() sunt continue pe
sunt continue pe ![]() ;
;
(2). functiile ![]() sunt
diferentiabile pe
sunt
diferentiabile pe ![]() ;
;
(3). ![]() ;
;
Atunci are loc inegalitatea
![]() . (34)
. (34)
38.
Corolar. Fie ![]() ,
, ![]() spatiu vectorial
normat si functia
spatiu vectorial
normat si functia ![]() . Daca
. Daca ![]() este continua pe
este continua pe ![]() , diferentiabila pe
, diferentiabila pe ![]() si
si ![]() , unde
, unde ![]() , atunci
, atunci
![]() . (35)
. (35)
Demonstratie. Alegem functia ![]() , definita prin
, definita prin ![]() . Atunci, din ipoteza, rezulta ca
. Atunci, din ipoteza, rezulta ca ![]() si din teorema
cresterilor finite, obtinem (35).
si din teorema
cresterilor finite, obtinem (35).
3
Corolar. Fie ![]() spatii vectoriale
normat,
spatii vectoriale
normat, ![]() o multime
deschisa si convexa si functia
o multime
deschisa si convexa si functia ![]() diferentiabila pe
diferentiabila pe ![]() . Atunci, oricare ar fi
. Atunci, oricare ar fi ![]() , are loc inegalitatea:
, are loc inegalitatea:
![]() . (36)
. (36)
Demonstratie. Fie ![]() , unde
, unde ![]() este multime
convexa. Atunci
este multime
convexa. Atunci ![]() contine segmentul
contine segmentul
![]() .
.
Consideram functia ![]() ,
, ![]() si functia
compusa
si functia
compusa ![]() . Atunci
. Atunci ![]() este
diferentiabila pe
este
diferentiabila pe ![]() si avem
si avem ![]() . Folosind observatia de mai jos obtinem:
. Folosind observatia de mai jos obtinem:
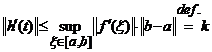 , unde
, unde ![]() .
.
Potrivit corolarului 38, avem ![]() , de unde se obtine inegalitatea (36).
, de unde se obtine inegalitatea (36).
40. Observatie.
Fie ![]() ,
, ![]() aplicatii lineare
si continue. Atunci
aplicatii lineare
si continue. Atunci ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |