Pentru graful G=(X,U), ![]() complet simetric si
fara bucle, elementele matricei
complet simetric si
fara bucle, elementele matricei ![]() cu proprietatile:
cu proprietatile:
a) ![]() ;
;
b) ![]()
reprezinta lungimile arcelor corespunzatoare ale grafului.
Sa se proiecteze un algoritm care sa execute operatiile:
Sa
genereze matricea ![]() a ponderilor minimale
pe linii si pe coloane a matricei
a ponderilor minimale
pe linii si pe coloane a matricei ![]() .
.
Utilizand matricea ![]() anterior generata sa
se genereze un circuit hamiltonian minimal
anterior generata sa
se genereze un circuit hamiltonian minimal ![]() asociat lui G si sa se
precizeze
asociat lui G si sa se
precizeze ![]() .
.
Pentru algoritmul proiectat sa se scrie un program corespunzator.
Sa se exemplifice textul temei pentru fiecare din cazurile urmatoare in parte, stiind ca elementele matricei A care intervine reprezinta lungimea arcelor corespunzatoare ale grafului considerat.
a) G=(X,U), ![]()

b) G=(X,U), ![]()
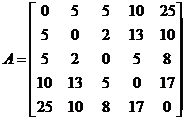
Descrierea algoritmului
1. Elementele ![]() si
si ![]() cu verificarea
proprietatilor din enunt fiind precizate, generarea elementelor matricei
cu verificarea
proprietatilor din enunt fiind precizate, generarea elementelor matricei ![]() se face astfel:
se face astfel:
pentru a nu se
produce confuzii, elementele diagonalei principale ![]() vor fi marcate
distinct "*"
vor fi marcate
distinct "*"
oricarui element ![]() , i<j I se asociaza numarul natural
, i<j I se asociaza numarul natural ![]() reprezentand numarul
elementelor matricei A aflate pe linia i si coloana j,
reprezentand numarul
elementelor matricei A aflate pe linia i si coloana j, ![]() care sunt strict mai
mici decat
care sunt strict mai
mici decat ![]() ;
; ![]()
La sfarsitul prelucrarii, tinand seama ca matricea e simetrica ![]()
![]() , se va obtine
, se va obtine ![]() a ponderilor naturale
minimale pe liniile si coloanele corespunzatoare elementelor matricii
a ponderilor naturale
minimale pe liniile si coloanele corespunzatoare elementelor matricii ![]() precizate.
precizate.
2.Pentru generarea unui circuit hamiltonian ![]() de lungime minima
de lungime minima ![]() se aplica algoritmul
descris la tema 7 considerand matricea B anterior generata. In acest sens la
sfarsitul prelucrarii se va obtine multimimea
se aplica algoritmul
descris la tema 7 considerand matricea B anterior generata. In acest sens la
sfarsitul prelucrarii se va obtine multimimea ![]() a elementelor
esential minimale si va fi precizat eventual un varf de
articulatie minima corespunzator grafului. Pentru fiecare element al
multimii
a elementelor
esential minimale si va fi precizat eventual un varf de
articulatie minima corespunzator grafului. Pentru fiecare element al
multimii ![]() generata se scriu
grafurile permutare
generata se scriu
grafurile permutare ![]() de valoare minima
de valoare minima ![]() .
.
Daca ![]() , atunci oricare din grafurile permutare distincte dintre
cele anterior generate care au aceleasi valori minime
, atunci oricare din grafurile permutare distincte dintre
cele anterior generate care au aceleasi valori minime ![]() (calculate cu
elementele matricei B) vor reprezenta circuitele hamiltoniene
(calculate cu
elementele matricei B) vor reprezenta circuitele hamiltoniene ![]() avand lungimea minima
avand lungimea minima ![]() (calculate cu
elementele matricei A) corespunzatoare grafului G considerat.
(calculate cu
elementele matricei A) corespunzatoare grafului G considerat.
Daca pentru orice element ![]() se defineste numarul
natural
se defineste numarul
natural ![]() ca reprezentand
numarul de elemente aflate pe linia I si coloana j in matricea A, elemente ce sunt mai mari
decat
ca reprezentand
numarul de elemente aflate pe linia I si coloana j in matricea A, elemente ce sunt mai mari
decat ![]() , atunci la sfarsitul prelucrarii se va obtine matricea
, atunci la sfarsitul prelucrarii se va obtine matricea ![]() a ponderilor maximale
pe linii si coloane corespunzatoare elementelor matricei
a ponderilor maximale
pe linii si coloane corespunzatoare elementelor matricei ![]() asociata grafului G.
asociata grafului G.
Utilizand algoritmul anterior
descris aplicat matricei ![]() astfel generata se va
obtine un circuit hamiltonian
astfel generata se va
obtine un circuit hamiltonian ![]() de lungime maxima
de lungime maxima ![]() corespunzatoare
grafului G.
corespunzatoare
grafului G.
Cazuri particulare
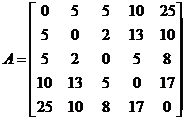
|
|
n |
v=(1,2,3,4,5) |
||||||
|
S: | ||||||||
|
S: |
v1=varf de articulatie
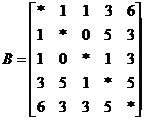
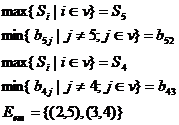
S = (11, 9, 14, 17)
![]()
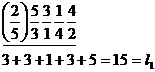
![]()
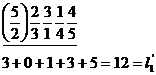
![]()
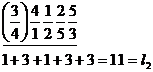
![]()
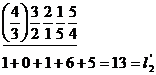
min=![]() =11
=11
![]()
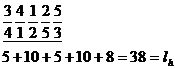
/* 8.c */
#include <stdio.h>
#include 'citire.h'
#include 'mtrxutil.h'
#include '7core.h'
#include 'citire.c'
#include 'mtrxutil.c'
#include '7core.c'
int main(void)
/* citire.h */
#ifndef __citire__
#define __citire__
#include <stdio.h>
#include <stdlib.h>
#define debug 1
#include 'mtrxutil.h'
int Citire(matrice *);
int CitireSimetrica(matrice *);
#endif
/* mtrxutil.h */
#ifndef __mtrxutil__
#define __mtrxutil__
#define MAXN 100
typedef struct slinielinie;
typedef struct smatricematrice;
/* source, dest */
void CopyMatrix(matrice *,matrice *);
int LungimeDrum(int *,int, matrice *);
int VerificaSimetrie(matrice *);
void MatriceaMare(matrice *,matrice *);
void PonderiMinimale(matrice *,matrice *);
void Tiparire(matrice *);
void ExtremalaInferioara(matrice *,matrice *);
int Egal(matrice *,matrice *);
#endif
/* 7core.h */
#ifndef __7__
#define __7__
#include 'citire.h'
typedef struct sEem Eem;
typedef struct sciclu ciclu;
typedef struct sbest best;
void Rezolvare7(matrice * a, Eem * b);
void PrintEem(Eem * e, const char *s);
void AfiseazaSolutii(best * sol);
void Cicluri(Eem * e, int n, matrice * a,best *solutii,int);
#endif
/* citire.c */
#include 'citire.h'
int Citire(matrice *a)
}
}
return(0);
int CitireSimetrica(matrice *a)
return(0);
/*mtrxutil.c*/
#include <stdio.h>
#include 'mtrxutil.h'
void CopyMatrix(matrice *a,matrice *b)
int Egal(matrice *a,matrice *b)
void Tiparire(matrice *a)
printf('n');
}
/* fake sqr */
#define SQR(a) ((a))
void ExtremalaInferioara(matrice *a,matrice *b)
b->a[i][j]=max;
}else
}
}
a- matrice simetrica
void PonderiMinimale(matrice *a,matrice *b)
else
}
}
void MatriceaMare(matrice *a,matrice *dest)
int LungimeDrum(int *b,int n, matrice *a)
int VerificaSimetrie(matrice *a)
/* 7core.c */
#include <stdio.h>
#include <stdlib.h>
#include 'citire.h'
#include '7core.h'
#ifndef debug
#define debug 0
#endif
Daca iau toate minimele de pe o linie , exista cazuri in care
algoritmul pare sa nu mearga (de fapt afiseaza ceva ce nu
pare corect).
Exemplu:
#define NU_TOATE_MINIMELE
int minim(int *a, int p, int n, int *v)
}
for (i = 0; i < n; i++)
}
return (a[j]);
void Rezolvare7(matrice * a, Eem * b)
}
an = n;
/* cat timp nu avem mai mic decat 3 repetam pasii */
while (an >= 3)
}
/* cautam acum toti maximii din s */
for (i = 0; i < n; i++)
if (p == k)
s[p] = s[p] - a->a[i][p] - a->a[k][p];
}
#ifdef NU_TOATE_MINIMELE
break;
#endif
}
}
}
}
}
/* verificam in care din cazurile n=1,2 suntem */
switch (an) else
}
}
break;
case 1:
b->p = 0;
for (i = 0; i < n; i++)
}
break;
default:
/* nu se poate ajunge aici (teoretic :) */
break;
}
void PrintEem(Eem * e, const char *s)
printf('n');
switch (e->p)
void AdaugaSolutie(int *b, int n, matrice * a, best * sol,int sign)
s += a->a[b[0]][b[n - 1]];
if (!((sol->solutii == NULL) || (sign * sol->best > sign * s)))
if(debug)
printf('n');
}
if ((sol->solutii != NULL) && (sign * sol->best > sign * s))
}
/* acum adaugam solutia gasita */
sol->best = s;
z = (ciclu *) malloc(sizeof(ciclu));
if (z == NULL)
for (i = 0; i < n; i++)
z->next = sol->solutii;
sol->solutii = z;
void AfiseazaSolutii(best * sol)
printf('%dn', a->a[0]+1);
}
int valid_a(int a, int x, int b, Eem * e)
break;
}
}
/* elementul x nu face parte dintr-o pereche Eem */
return (1);
int valid(int *b, int k, Eem * e, int n)
}
for (i = 1; i < k; i++)
}
if (k == n - 1)
if (!valid_a(b[k], b[0], b[1], e))
}
return (1);
void Cicluri(Eem * e, int n, matrice * a,best *solutii,int sign)
int k = 1, ok, i;
solutii->n=n;
solutii->solutii=0;
solutii->best=0;
b[0] = 0;
b[k] = -1;
while (k > 0)
printf('n');
}
ok = 0;
while ((!ok) && (b[k] < n - 1))
if (ok)
printf('n');
}
} else
} else
}
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |