Ciocnirea corpurilor
Ciocnirea reprezinta un proces mecanic in care interactia dintre corpurile care se ciocnesc dureaza un timp foarte scurt (finit).
In momentul atingerii corpurilor care se ciocnesc, viteza lor relativa se reduce la zero, iar energia cinetica relativa se transforma in energie de deformare sau alte forme de energie. Dupa ciocnire, deformatiile corpurilor se reduc, viteza relativa creste si energia cinetica relativa se restituie partial.
Daca deformatiile de dupa ciocnire dispar si energia cinetica relativa se restituie integral, fara a se transforma in alte forme de energie, ciocnirea se numeste elastica. Daca deformatiile nu se anuleaza si energia cinetica relativa nu se restituie integral corpurilor, atunci ciocnirea este neelastica. Daca in procesul de ciocnire corpurile fuzioneaza, atunci ciocnirea este total neelastica si evident in acest caz corpurile se vor misca impreuna dupa ciocnire.
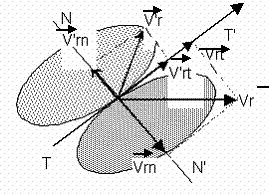 Fie doua corpuri nepunctiforme care se coicnesc
si fie TTī planul tangent (de contact) al acestora. Directia NNī perpendiculara
pe planul de contact se numeste directie sau linie de ciocnire.
Fie doua corpuri nepunctiforme care se coicnesc
si fie TTī planul tangent (de contact) al acestora. Directia NNī perpendiculara
pe planul de contact se numeste directie sau linie de ciocnire.
 Daca linia de ciocnire NNī trece in momentul
ciocnirii prin centrele de masa ale celor doua corpuri, ciocnirea se
numeste centrica, in caz
contrar ciocnirea se numeste necentrica.
Daca linia de ciocnire NNī trece in momentul
ciocnirii prin centrele de masa ale celor doua corpuri, ciocnirea se
numeste centrica, in caz
contrar ciocnirea se numeste necentrica.
Daca inainte de ciocnire corpurile se miscau dupa linia de ciocnire NNī ciocnirea se numeste frontala, in caz contrar ea se numeste oblica. Se poate spune ca daca corpurile sunt sfere omogene, ciocnirea acestora este totdeauna centrica dar in general oblica.
Daca ![]() si
si ![]() sunt vitezele corpurilor fata de Pamant
inainte de ciocnire, atunci viteza relativa de ciocnire (viteza corpului 1
fata de corpul 2) va fi:
sunt vitezele corpurilor fata de Pamant
inainte de ciocnire, atunci viteza relativa de ciocnire (viteza corpului 1
fata de corpul 2) va fi:
![]() (1.65)
(1.65)
Descompunem viteza relativa dupa doua directii perpendiculare, dupa directia liniei de ciocnire si dupa o directie perpendiculara pe aceasta continuta in planul de contact:
![]() (1.66)
(1.66)
Dupa ciocnire componenta ![]() isi schimba
semnul, deoarece inainte de ciocnire corpurile se apropie, iar dupa
ciocnire acestea se indeparteaza. Componenta vitezei relative din
planul de contact, in cazul unei
ciocniri perfect elastice, nu se modifica.
isi schimba
semnul, deoarece inainte de ciocnire corpurile se apropie, iar dupa
ciocnire acestea se indeparteaza. Componenta vitezei relative din
planul de contact, in cazul unei
ciocniri perfect elastice, nu se modifica.
In general insa, prin ciocnire,
deoarece corpurile nu sunt nici perfect elastice si nici absolut netede,
cele doua componente ale vitezei relative se modifica. Astfel,
componenta normala a vitezei relative de dupa ciocnire ![]() este in modul mai mica decat
este in modul mai mica decat ![]() , deoarece corpurile nu sunt perfect elastice. In ceea ce
priveste componenta vitezei din planul de contact, aceasta se
micsoreaza din cauza frecarii, astfel ca dupa ciocnire
, deoarece corpurile nu sunt perfect elastice. In ceea ce
priveste componenta vitezei din planul de contact, aceasta se
micsoreaza din cauza frecarii, astfel ca dupa ciocnire
![]() . (vezi figura 1.12)
. (vezi figura 1.12)
In procesul de ciocnire se exercita forte de interactiune intre corpuri, deci forte interne, dar acestea nu pot schimba impulsul total si momentul cinetic total ale sistemului mecanic. In intervalul de timp foarte scurt cat dureaza ciocnirea, variatia de impuls si variatia de moment cinetic produse de eventuale forte externe, se pot neglija in comparatie cu variatiile de impuls si de moment cinetic produse de fortele interne, care desi dureaza putin, sunt mult mai mari decat fortele obisnuite externe. De aceea impulsul si momentul cinetic ale sistemului de corpuri care se ciocnesc se conserva in procesul de ciocnire.
Ciocnirea plastica
Ciocnirea plastica este o ciocnire total neelastica a doua corpuri care se cupleaza, si care se deplaseaza cu aceeasi viteza dupa ciocnire.
Fie m1 si m2 masele corpurilor si ![]() ,
, ![]() vitezele inainte de
ciocnire. Atunci din legea conservarii impulsului rezulta:
vitezele inainte de
ciocnire. Atunci din legea conservarii impulsului rezulta:
![]() (1.67)
(1.67)
de unde obtinem viteza dupa ciocnire a corpurilor
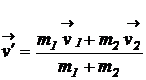 (1.68)
(1.68)
Energia cinetica pierduta, transformata in alte forme de energie (de obicei sub forma de caldura) va fi:
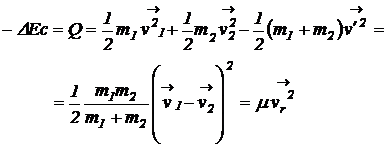 (1.69)
(1.69)
unde:
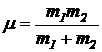 (1.70)
(1.70)
se numeste masa redusa a celor doua corpuri, iar
![]() (1.71)
(1.71)
este viteza relativa de ciocnire.
2 Ciocnirea perfect elastica
In acest caz se conserva pe langa impulsul total si energia cinetica totala. Considerand ciocnirea centrica si centrala vom avea:
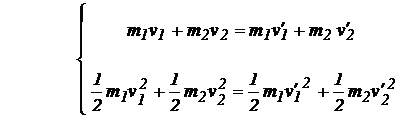 (1.72)
(1.72)
de unde:
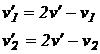 (1.73)
(1.73)
unde
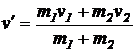 (1.74)
(1.74)
Ciocnirea cu un perete
In cazul ciocnirii centrice, perfect elastice si frontale, considerand peretele ca un corp cu masa foarte mare (m2 >> m1) atunci din (1.74) avem:
![]() (1.75))
(1.75))
Consideram
un perete in repaus adica ![]() si in acest caz din (1.75) avem ca
si in acest caz din (1.75) avem ca![]() ,
,![]() , adica corpul 1 se va intoarce inapoi cu
aceeasi viteza (in modul).
, adica corpul 1 se va intoarce inapoi cu
aceeasi viteza (in modul).
Pentru o ciocnire oblica , perfect elastica, cu un perete in repaus, ca in figura 1.13, vom avea:
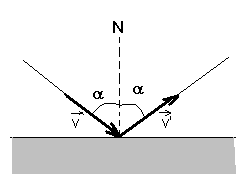
Figura 1.13 Ciocnirea oblica
![]() (1.76)
(1.76)
si deci
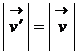 (1.77)
(1.77)
In acelasi timp se mai poate spune ca ![]() adica unghiul de
incidenta este egal cu unghiul de reflexie.
adica unghiul de
incidenta este egal cu unghiul de reflexie.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |