Determinarea pozitiei si a traiectoriei unui punct material
Traiectoria unui punct material este curba descrisa de acesta in decursul miscarii sale, adica locul geometric al pozitiilor succesive prin care trece mobilul in decursul miscarii. In mecanica clasica se considera ca traiectoria mobilului este bine determinata, iar multimea pozitiilor succesive ocupate de acesta in decursul miscarii este continua.
Pozitia
unui punct material (mobil), M, la un moment dat pe traiectoria sa este
precizata prin asa-numitul vector
de pozitie 
, un vector care isi are originea in originea reperului
ales, iar varful coincide cu punctul material studiat. Legea de miscare a
mobilului este exprimata generic prin ecuatia vectoriala:
.
Deplasarea punctului M intre doua pozitii succesive M1 si M2
de pe traiectoria sa, considerate la momentele t1 si t2,
definite prin vectorii de pozitie 
si 
, este data de vectorul
deplasare:
.
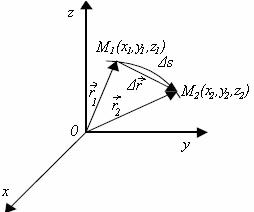
Fig. 2.1. Vectorul de pozitie si vectorul deplasare
Miscarea unui punct material poate fi descrisa intr-un sistem de coordonate tridimensional drept (cartezian) (Fig. 2.2.a), intr-un sistem de coordonate cilindrice (Fig. 2.2.b), sau intr-un sistem de coordonate sferice (Fig. 2.2.c).
Intr-un sistem de coordonate carteziene, x, y, z, se poate scrie:
.Intre coordonatele carteziene (x, y, z) si cele cilindrice (ρ, φ, z) exista urmatoarele formule de transformare:
, 
, 
, .
Formulele de trecere directa si inversa de la coordonatele carteziene (x, y, z) la cele sferice (ρ, φ, θ) sunt:
, 
, 
, 
.
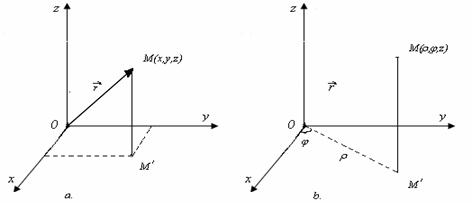
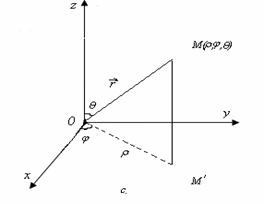
Fig. 2.2. Sisteme de coordonate: a. cartezian; b. coordonate cilindrice;
c. coordonate sferice
Miscarea punctului material este
descrisa de variatia in timp a coordonatelor sale spatiale 
, 
, 
(carteziene, cilindrice sau sferice). Ecuatiile 
, unde t = 1, 2, 3
se numesc ecuatii parametrice
ale miscarii (parametrul fiind timpul t).
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
