|
(2) Esantionarea Prelevarea la intervale de timp
prestabilite (t) numite perioade de esantionare
(1 . 2 ore) a unui numar de
esantioane (selectii) (n1) alcatuite
dintr-un numar de produse (n2) prestabilit din cadrul
lotului.
In cazul de
fata, s-a considerat:
t =1 ora;
n1= 6 esantioane;
n2 = 5 buc.
(3) Masurarea: Masurarea cu mijloace adecvate a dimensiunii
care intereseaza. Astfel, raportul dintre precizia (i) mijlocului
de masurare si toleranta dimensionala (TL)
considerata trebuie sa satisfaca relatia:
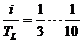 (4.7) (4.7)
In exemplul
considerat, se masoara cele cinci diametre efective din cadrul
fiecaruia din cele sase esantioane (selectii) prelevate
la intervalele de esantionare considerate (1 ora) cu ajutorul unui
micrometru la care i=0,01 mm, iar rezultatele masuratorilor
se noteaza la rubrica Date primare (x) " din tabelul 4.1.
(4) Prelucrarea datelor primare Se calculeaza urmatorii
parametri:
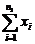 - suma valorilor masurate in cadrul fiecarui esantion; - suma valorilor masurate in cadrul fiecarui esantion;
In cazul de fata, se insumeaza cele cinci
valori ale diametrelor efective determinate, corespunzatoare
fiecarui esantion. Rezultate obtinute se noteaza in
coloana corespunzatoare din tabelul 4.1
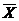 - media valorilor obtinute prin masurare din cadrul
fiecarui esantion pe baza relatiei: - media valorilor obtinute prin masurare din cadrul
fiecarui esantion pe baza relatiei:
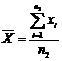 (4.8) (4.8)
Rezultatele obtinute se noteaza in
coloana 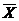 din tabelul 4.1. din tabelul 4.1.
R - amplitudinea valorilor din cadrul unui esantion
(selectii) cu ajutorul formulei:
R= xmax
- xmin
unde:
xmax reprezinta valoarea maxima din cadrul
esantionului;
xmin - valoarea minima din cadrul
esantionului.
Valorile obtinute se inscriu in coloana R din
tabelul 4.1.
(5) Calculul parametrilor statistici Se calculeaza urmatorii
parametri statistici:
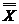 - media procesului
(media mediilor) pe baza relatiei: - media procesului
(media mediilor) pe baza relatiei:
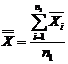 (4.10) (4.10)
In acest caz: 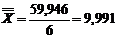
|
Esantionarea
Masurarea
Precizia de citire =
fractiune din toleranta prescrisa
|
|
Abaterea medie patratica
Tabelul 4.2. Extras din STAS 3160-84
|
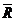 - media amplitudinilor cu ajutorul relatiei: - media amplitudinilor cu ajutorul relatiei:
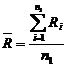 (4.11) (4.11)
In
exemplul de fata:
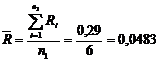 mm mm
Abaterea
medie patratica () se calculeaza cu ajutorul formulei:
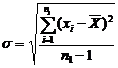 (4.12) (4.12)
In
practica, abaterea medie patratica (se
determina mai rapid pe baza formulei:
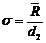 (4.13) (4.13)
unde d2 este un factor de
conversie stabilit de standarde in functie de marimea
esantionului n.
In tabelul
4.2, se prezinta un extras din STAS 3160-84
|
|
Trasarea curbei lui Gauss
Fig. 4.2.
Curba lui Gauss
|
In cazul
de fata, pentru marimea esantionului n=5, d2=2,326
si astfel abaterea medie patratica este:
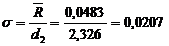 mm mm
Dispersia
valorilor (6) este in acest caz:
6
= 6 . 0,0207=0,1246 mm
(6) Trasarea curbei lui Gauss
Se
traseaza curba lui Gauss pe care se inscriu valorile parametrilor
statistici calculati precum si datele initiale (fig. 4.2).
|
|
(7) determinarea
capabilitatii si stabilitatii procesului
Capabilitatea procesului se determina cu ajutorul
relatiei (4.3). In acest caz:
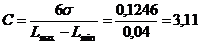
Avand in vedere
valoarea parametrului C si dispunerea curbei lui Gauss din figura
4.2, concluziile referitoare la
capabilitatea procesului (masinii) preciziei si reglajului sunt
urmatoarele:
Procesul nu are
capabilitatea necesara (nu asigura precizia prescrisa - v.
relatia (4.6)):
C=3,11>0,8
Procesul este instabil
ca precizie deoarece:
w = 6 = 0,12 > TL= 0,04
Procesul este instabil
ca reglaj:
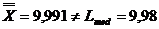
(8) Stabilirea procentului
estimat de rebut: Se calculeaza limitele repartitiei
populatiei Xmax si Xmin:
Xmax
=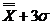 (4.14) (4.14)
Xmin
=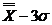 (4.15) (4.15)
In exemplul de
fata:
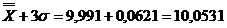
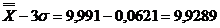
Argumentele zs
si zi functiei normale (integrale) Laplace
corespunzatoare valorilor limita superioara Lmax
si inferioara Lmin prescrise sunt:
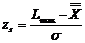 (4.16) (4.16)
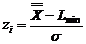 (4.17) (4.17)
In acest caz,
valorile obtinute sunt:
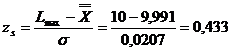
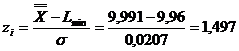
Procentele
estimate de rebut Ps si Pi
corespunzatoare limitelor superioara Lmax si
inferioara Lmin se stabilesc cu ajutorul formulelor:
|
determinarea
capabilitatii si stabilitatii procesului
Concluzii privind capabilitatea si stabilitatea
Stabilirea procentului estimat
de rebut
|
|
|
Ps
= 0,5 - (zs) (4.18)
Pi
= 0,5 - (zi) (4.19)
Din tabelul 4.8,
valorile functiei normale (integrale) Laplace (z) a
semicurbei normale pentru valorile argumentelor zs
si zi sunt:
(
zs)= 0,16640
( zi)=
0,43189
Prin urmare,
procentele estimate de rebut sunt:
Ps = 0,5 - (zs) = 0,5 - 0,16640 =
0,3336=33,36%
Pi = 0,5 - (zi) = 0,5 - 0,43189 =
0,0681=6,81%
Procentul total
de rebut se determina:
Ptotal = Ps Pi
In cazul de fata:
Ptotal = Ps Pi
Solutie Se apeleaza la un procedeu de prelucrare (strunjire de
semifinisare, rectificare de degrosare etc.) care asigura o
treapta superioara de precizie (treapta 9, stabilita pe baza
tolerantei prescrise TL = 0,04 mm la dimensiunea
nominala 10 din tabelul de tolerante fundamentale).
Se regleaza scula la cota pentru
obtinerea stabilitatii reglajului: 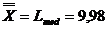
Pentru
acesta, dimensiunea optima de reglare a sculei la cota dro
este:
dro = Lmin+ 3
unde: este eroarea de reglare,
= 2 . 5 m sau = (1 . 3)
iar corespunde evident noului
proces adoptat, cu precizie mai mare (strunjire de semifinisare, rectificare
de degrosare etc.
|
| | |
Tabelul 4.8. Valorile functiei normale (integrale) Laplace
(z)
|
Controlul operativ
Esantionare
Masurare
Informatii privind stabilitatea
Limitele de control
pentru medie
pentru amplitudine
Coeficienti standardizati
|
4.3. Controlul statistic al proceselor
pentru caracteristici masurabile
Aplicarea controlului statistic pe
flux de fabricatie, pentru caracteristici
masurabile permite prin interpretarea rezultatelor, evaluarea in
orice moment a valorilor caracteristicilor de calitate ale produselor. In
functie de rezultatele controlului statistic, se pot intreprinde actiuni preventive care sa
evite aparitia neconformitatilor.
Controlul statistic pe flux de fabricatie consta in
prelevarea direct din fluxul de fabricatie a unui numar de esantioane (selectii) la anumite intervale de timp bine determinate
(1 . 8 ore). Fiecare esantion
contine un numar de produse
(n = 2 . 12 bucati) prelevate in ordinea fabricatiei.
Se masoara valorile caracteristicii de calitate controlate a
produselor prelevate si se determina: media aritmetica
a valorilor masurate si amplitudinea valorilor.
Aceste rezultate furnizeaza informatii asupra stabilitatii
reglajului si preciziei procesului (echipamentului).
Pentru a se evita destabilizarea procesului in intervalul dintre
doua esantionari, rezultatele masuratorilor nu se
pot compara cu limitele prescrise maxima (Lmax)
si minima (Lmin) pentru caracteristica
controlata ci cu limite mai stranse - limitele de control.
Conform standardelor, acestea se stabilesc conform relatiilor de mai
jos.
Limitele de control pentru medie:
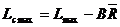 (4.21) (4.21)
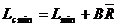 (4.22) (4.22)
Limitele de control pentru amplitudine:
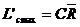 (4.23) (4.23)
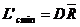 (4.24) (4.24)
In formulele 4.21 . 4.24, 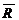 este media amplitudinilor care se calculeaza cu
formula: este media amplitudinilor care se calculeaza cu
formula:
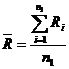 (4.25) (4.25)
unde:
Ri
este amplitudinea corespunzatoare fiecarui esantion;
n1
- numarul de esantioane considerate.
Coeficientii B, C, D
din formulele 4.21 . 4.24 sunt stabiliti de standarde (v. tabelul 4.4),
iar valorile lor depind de numarul produselor (n) din cadrul unui
esantion.
|
Tabelul 4.4. Coeficienti pentru calculul limitelor de
control (Extras din STAS
3160-84)
|
In vederea aplicarii metodei, se foloseste "fisa de control 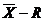 ", tabelul 4.5, parcurgandu-se mai multe etape: ", tabelul 4.5, parcurgandu-se mai multe etape:
Exemplu: Pentru produsul cutie de chibrituri, se
aplica controlul statistic in flux pentru caracteristica - numarul de bete din interiorul
cutiei.
(1) Date
initiale:
Limita
superioara: Lma x= 210 bete
Limita
inferioara: Lmin =
190 bete
Marimea
esantionului: n = 5 cutii
Perioada
de esantionare: t= 2 ore
(2) Stabilirea
limitelor de control : Pe baza formulelor 4.21 si 4.22, se determina
limita de control maxima Lcmax si
limita de control minima Lcmin pentru valoarea medie 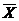 : :
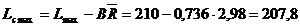
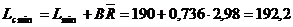
unde:
coeficientul B = 0,736 pentru marimea esantionului n
= 5 (v. tabelul 4.4);
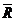 este amplitudinea medie a procesului pentru o perioada
de referinta. S-a considerat este amplitudinea medie a procesului pentru o perioada
de referinta. S-a considerat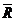 =2,98. =2,98.
Se determina de asemenea, limita de control maxima L'cmax
si limita de control minima L'cmin pentru
amplitudinea R conform formulelor 4.22 si 4.23:
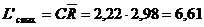 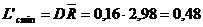
unde:
coeficientii C = 2,22, D = 0,16 pentru n = 5 (v.
tabelul 4.4).
Pe fisa de control 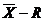 " (tabelul 4.5), se
traseaza cele patru drepte orizontale corespunzatoare limitelor
de control stabilite anterior. " (tabelul 4.5), se
traseaza cele patru drepte orizontale corespunzatoare limitelor
de control stabilite anterior.
(3) Masurarea:
Se determina
valoarea caracteristicii controlate pentru produsele din esantioanele
prelevate la intervalele de esantionare stabilite.
In exemplul de fata, se determina numarul de
bete din fiecare din cele cinci cutii ale esantioanelor prelevate
de pe fluxul de fabricatie la intervalul de doua ore. Rezultatele
se noteaza in tabelul 4.5 la rubrica - Valoarea caracteristicii
masurate X.
(4) Calculul
mediei si amplitudinii: Se calculeaza media 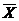 corespunzatoare
fiecarui esantion prelevat pe baza formulei: corespunzatoare
fiecarui esantion prelevat pe baza formulei:
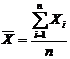 (4.26) (4.26)
Se determina amplitudinea valorilor
caracteristicii de calitate masurate corespunzatoare fiecarui
esantion:
R = Xmax - Xmin (4.27)
unde Xmax,
Xmin sunt valorile maxime si minime din fiecare
esantion prelevat.
|
Etape
Date intiale
Limite de control
pentru medie
pentru amplitudine
Trasarea limitelor de control
Masurarea
Media pe fiecare esantion
Amplitudinea pe fiecare
esantion
|
|
Rezultatele pentru exemplul
de fata au fost notate la rubricile - Suma, Media, Amplitudinea.
Valorile calculate ale mediei si amplitudinii au fost reprezentate
grafic.
Liniile centrale ale graficelor sunt 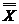 (media procesului)
si (media procesului)
si 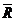 (amplitudinea medie)
si se calculeaza cu formulele de mai jos. (amplitudinea medie)
si se calculeaza cu formulele de mai jos.
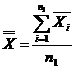 (4.28) (4.28)
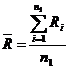 (4.29) (4.29)
Pentru exemplul de fata,
acesti parametri au valorile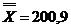 ; ; 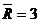
(5) Interpretarea
rezultatelor: Analiza abordeaza succesiv graficul R si 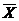 : :
I) Daca valorile amplitudinii R
se incadreaza intre limitele de control L'cmax si
L'cmin, procesul este stabil
ca precizie
Daca R > L'cmax atunci
procesul este instabil ca precizie;
In cazul in care, R < L'cmin
atunci procesul este prea precis;
utilizarea masinii (echipamentului) nu
este rationala in raport cu limitele prescrise (este
folosita neeconomic).
II) Daca valorile mediei 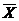 se situeaza intre cele doua limite de control
Lcmax si Lcmin, procesul
este stabil ca reglaj; se situeaza intre cele doua limite de control
Lcmax si Lcmin, procesul
este stabil ca reglaj;
In caz contrar, procesul este instabil ca reglaj.
Observatii
privind interpretarea graficului R:
a) Un proces este sub control daca
punctele sunt distribuite aleatoriu
intre limitele de control;
b) Punctele in afara limitelor indica existenta unor cauze
speciale care se cer investigate
imediat;
c) Un punct peste limita de control
superioara poate arata
ca:
limitele de control sau punctul au fost calculate gresit;
variabilitatea procesului a crescut
in acel punct accidental sau ca urmare a unei tendinte;
a fost schimbat sistemul de masurare
(aparatul) sau operatorul
d) Un punct sub limita de control inferioara poate indica:
o eroare de calcul a limitei de control sau a punctului;
schimbarea sistemului de
masurare sau a operatorului;
dispersia procesului este mai
mica (precizia a crescut);
e) O serie de sapte puncte deasupra liniei centrale sau cu valoare crescatoare poate indica:
cresterea dispersiei
datorita unor disfunctii ale procesului;
modificarea unuia din elementele
procesului;
modificarea sistemului de
masurare;
f) O serie de sapte puncte sub linia
centrala poate arata:
o scadere a
variabilitatii procesului, o imbunatatire care trebuie
conservata;
modificarea sistemului de
masurare
|
Rezultate
Liniile centrale
pentru medie
pentru amplitudine
Stabilitatea preciziei
Stabilitatea reglajului
Interpretarea graficului R si 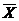
|
|
Aplicarea regulilor de interpretare
|
g) Un numar de 25 de puncte sau peste 70% se afla
in treimea centrala a zonei de control aratand ca:
exista erori de calcul sau
de reprezentare a punctelor sau limitelor de control;
esantionul are in
componenta elemente din mai multe fluxuri;
h) In mod normal, circa 2/3 din punctele graficului R se
afla in treimea centrala a domeniului delimitat de limitele de
control si 1/3 in cele doua treimi marginale.
Aceleasi
reguli de interpretare (observatii)
privind dispunerea punctelor se aplica si la analiza 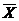 . .
Pentru exemplul de fata, se pot trage
urmatoarele concluzii:
(a) In ceea ce
priveste variatia amplitudinii R, aceasta se situeaza intre limitele de control L'cmax si L'cmin prin
urmare, procesul este stabil ca precizie. In intervalul orar 12 - 14
(esantioanele 3, 4), se observa chiar o crestere a preciziei (scadere a
variabilitatii procesului).
(b) Analizand
valorile 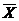 , se observa ca exista tendinta de apropiere de limita
maxima de control si chiar de depasire (cazul
esantionului nr. 5). Solutia consta in reducerea intervalului
de timp la care se realizeaza reglajul si reglarea masinii mai
aproape de limita minima de control pentru a utiliza mai eficient campul
de toleranta permis , se observa ca exista tendinta de apropiere de limita
maxima de control si chiar de depasire (cazul
esantionului nr. 5). Solutia consta in reducerea intervalului
de timp la care se realizeaza reglajul si reglarea masinii mai
aproape de limita minima de control pentru a utiliza mai eficient campul
de toleranta permis
Alte formule de
calcul pentru limitele de control
◘ pentru medie 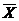 : :
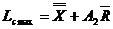 (4.30) (4.30)
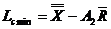 (4.31) (4.31)
◘ pentru amplitudine R:
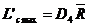 (4.32) (4.32) 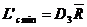 (4.33) (4.33)
Coeficientii
din formulele 4.31 - 4.33 se stabilesc pe baza marimii esantionului
n.
|
| | |
Tabelul
4.6. Coeficienti standardizati pentru calculul limitelor de control
|
4.4. CONTROLUL STATISTIC al proceselor PENTRU
CARACTERISTICI EXPRIMATE PRIN ATRIBUTE
Controlul
statistic pentru caracteristici exprimate prin atribute se
poate aplica in cazul oricarui tip de proces la care caracteristicile
pot avea doua valori
corespunzatoare celor doua stari: acceptat/neacceptat,
admis/respins, prezent/absent, trece/ nu trece etc.
Pentru
realizarea controlului, se determina ca si in cazul celui pentru
caracteristici masurabile, pozitiile
liniei centrale si limitelor de control superioare si inferioare.
Se
utilizeaza mai multe metode
pentru determinarea liniei centrale
si a limitelor de control:
proportia
de unitati neconforme (p);
numarul
de unitati neconforme (np);
numarul
de neconformitati (c);
numarul
de neconformitati pe unitate de produs (u).
Fiecareia
dintre aceste metode, ii corespund formule
specifice pentru determinarea liniei centrale si a limitelor de control.
In functie de metoda adoptata, se
pot controla:
□ esantioane de marime constanta (n) sau
□ esantioane de marime variabila (n1, n2, . . ,
nk),
k fiind numarul de esantioane.
Analiza
stabilitatii procesului se efectueaza dupa aceleasi
reguli (observatii) ca si la controlul statistic pentru
caracteristici masurabile.
In
continuare, se prezinta comparativ, exemple de aplicare a doua
metode de control statistic mentionate anterior: Metoda "p"- proportia
de unitati neconforme si
Metoda "c"- numarul de neconformitati.
Exemplul 1 Se aplica controlul statistic pentru caracteristici exprimate
prin atribute utilizand Metoda "p",
in cazul fabricatiei unui circuit integrat (BI 004).
Se controleaza zilnic, la un interval
de o ora un esantion de marime constanta n = 500 buc. Proportia de
unitati neconforme constatate pe
parcursul unei zile de lucru (doua schimburi) a fost notata in
tabelul 4.6.
Linia centrala si limitele de control se determina cu
ajutorul urmatoarelor formule:
linia
centrala:
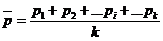 (4.30) (4.30)
unde:
pi
reprezinta proportia de unitati neconforme constatate
in cazul esantionul i;
k
- numarul de esantioane.
limita
de control superioara pentru proportia de unitati
neconforme:
 (4.31) (4.31)
|
Caracteristici exprimate prin
atribute
Metode pentru determinarea liniei
centrale si limitelor de control
Aceleasi reguli de interpretare
a rezultatelor
Comparatie intre doua
metode
Formule de calcul pentru
Linia centrala
Limitele de control
|
|
Reprezentarea grafica
Concluzii si solutii de
imbunatatire
Tema: Utilizand
graficul in Excel (tab. 4.6), cum ar trebui stabilite limitele de control
pentru perioada urmatoare pentru a conserva imbunatatirea
din intervalul 13-19
Formule de calcul pentru
Linia centrala
Limitele de control
|
limita de control inferioara:
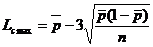 (4.32) (4.32)
In exemplul de fata, parametrii determinati cu ajutorul
formulelor 4.30 - 4.32 au valorile:
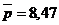
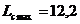
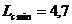
Au fost trasate linia
centrala si limitele de control pe graficul din tabelul 4.6. De
asemenea, a fost trasat graficul proportiei
de unitati neconforme (pi) pentru fiecare
esantion.
Concluzii:
Numarul de neconformitati se incadreaza
in limitele de control cu exceptia esantioanelor 5 (ora 12) si
14 (ora 21), la care s-a depasit limita de control superioara.
In general, se observa ca numarul de neconformitati
se situeaza sub linia centrala ceea ce conduce la concluzia ca
procesul de fabricatie decurge in bune conditii,
depasirea limitei de control in cazul celor doua
esantioane avand caracter accidental (indisciplina
tehnologica, schimbarea operatorului, a sistemului de control etc.). In
intervalul orar 13-19, se observa o scadere a
variabilitatii procesului - o imbunatatire care
trebuie conservata.
Exemplul 2 Se aplica controlul statistic pentru caracteristici exprimate
prin atribute utilizand Metoda "c",
in cazul fabricatiei aceluiasi circuit integrat (BI 004).
Se controleaza zilnic, la un interval
de o ora un esantion de marime constanta n = 500 buc. Numarul de
neconformitati constatate pe intreg intervalul monitorizat a fost
notat in tabelul 4.7.
Linia
centrala si limitele de control se determina cu ajutorul
urmatoarelor formule:
linia centrala:
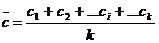 (4.33) (4.33)
unde:
ci
reprezinta numarul de neconformitati constatate in
cazul esantionul i;
k
- numarul de esantioane.
limita
de control superioara pentru numarul de
neconformitati:
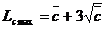 (4.34) (4.34)
limita
de control inferioara:
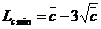 (4.35) (4.35)
|
|
Parametrii
determinati cu ajutorul formulelor 4.33 - 4.35 au valorile:
cmed
Lcmax
Lcmin
Au fost trasate linia
centrala si limitele de control pe graficul din tabelul 4.6. De
asemenea, a fost trasat graficul numarului de neconformitati (ci)
pentru fiecare esantion.
Concluzii: Numarul de neconformitati se incadreaza
in limitele de control cu exceptia esantioanelor corespunzatoare
intervalului orar 12 - 15, in care s-a depasit limita de control
superioara. Instabilitatea din acest interval nu are caracter
accidental. Ea poate fi determinata de actiunea cumulata a mai
multor elemente ale sistemelor tehnologice.
Inainte si dupa acest interval,
procesul are stabilitate, variabila
monitorizata (c) avand valori situate chiar sub linia centrala. In
intervalul orar 18 - 24, se constata o crestere a
stabilitatii care ar trebui conservata, in perioada
urmatoare prin retrasarea limitelor de control
|
Reprezentarea grafica
Concluzii si solutii de
imbunatatire
Tema: Utilizand
graficul in Excel (tab. 4.7), cum ar trebui stabilite limitele de control
pentru perioada urmatoare pentru a conserva imbunatatirea
din intervalul 18-24
|
| | |
Control statistic pe baza de
AQL
Definitie
Aplicabilitate
Plan de verificare
Riscuri ale controlului statistic al
produsului
Solutii pentru reducerea
riscurilor
Fig. 4.3.
Curba
operativa
|
4.5. CONTROLUL STATISTIC al produsului (CSP)
4.5.1. Caracteristici CSP
Controlul statistic al produsului se mai numeste si controlul
statistic la receptia loturilor de produse pe baza nivelului de calitate
acceptabil (Acceptable Quality Level - AQL).
AQL reprezinta procentul maxim de
produse neconforme sau numarul maxim de neconformitati
la o suta de unitati de produs pentru care lotul se considera acceptabil.
In Romania, controlul statistic
pe baza de AQL este reglementat de standardele SR ISO 2859 - 0
si SR ISO 2859 - 3.
Se aplica la receptia
furnizor-client - inainte de livrare sau la receptia
produselor:
indiferent daca clientul este
intern sau extern;
atat in cazul caracteristicilor masurabile (1) cat si in cazul celor exprimate prin atribute (2).
In ambele cazuri (1) si (2), este necesara elaborarea unui plan
de verificare care consta din:
q
planul de esantionare
q
regulile necesare pentru decizia de acceptare sau respingere in
functie de nivelul calitatii lotului.
Planul de verificare de multe ori imbraca forma unei proceduri
ce cuprinde scopul, domeniul de aplicare, definitii,
continutul, responsabilitatile, formularele tip utilizate
etc.
Controlul statistic presupune inspectia unui esantion - numar
de n produse din cadrul unui lot N. Intrucat n << N, iar concluziile
se refera la intreg lotul de produse N, exista
urmatoarele riscuri:
- riscul furnizorului ()
- de a se respinge lotul desi la un control integral, acesta ar
putea avea o calitate acceptabila;
- riscul clientului () - de a se
accepta lotul desi la un control integral, acesta ar putea avea o
calitate neacceptabila.
Riscurile si
si pot fi diminuate sau reduse la zero daca:
- se intreprind masuri
pentru stabilizarea procesului ale carui iesiri constituie
produsele controlate;
- se stabilesc corect
caracteristicile planului de verificare.
Se defineste fractiunea
defectiva conform relatiei:
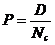 (4.33) (4.33)
unde: D este numarul
defectivelor (neconformitatilor);
Nc
este numarul de produse controlate.
|
Graficul care reprezinta
functia probabilitatii
de acceptare Pa in raport cu fractiunea
defectiva P se numeste curba operativa
(fig. 4.3) si caracterizeaza
operatia de control statistic. Odata cu cresterea
defectivelor probabilitatea de acceptare scade.
Curba operativa
prezinta patru puncte
caracteristice:
Punctul (1) de coordonate P=0%
si Pa=100%. Daca esantionul nu contine defective (P=0),
probabilitatea de acceptare este Pa=100% (Pa=1).
Punctul (2) de coordonate P=100% si Pa=0%. Daca
esantionul contine 100% defective, probabilitatea de acceptare este
Pa=0%.
Punctul (riscul furnizorului) de
coordonate P=AQL si Pa=100-%. Daca
esantionul contine o
proportie de defective P<AQL (nivel de
calitate accceptabil), probabilitatea de acceptare este Pa>100-%. In
general, se considera = 0,05 (5%) deci Pa>95%.
Se recomanda
Punctul (riscul clientului) de
coordonate P=LQ (nivel de calitate tolerata) si Pa=%.
Daca esantionul contine o proportie de defective D>LQ, probabilitatea de acceptare
este Pa<%. In general, se considera
= 0,1 (10%) si deci probabilitatea de acceptare a lotului care are
defective mai multe decat nivelul de calitate tolerat este Pa<10%.
Se recomanda = 0,05 . 0,1 deci un risc mai mare pentru
client in raport cu acela al furnizorului.
Curba operativa ideala este o curba in scara (linia
punctata, fig. 4.3). Pe baza acestei caracteristici, toate loturile vor
fi acceptate daca proportia
de defectivelor P este mai mica decat AQL, iar cele care
au P mai mare decat AQL vor fi respinse. Aceasta
curba se poate obtine numai prin controlul integral al
lotului (100%), prin urmare nu are
aplicabilitate practica.
Exista o familie de curbe operative (v. STAS 3160-84.
Procedee si curbe statistico-matematice pentru verificarea
calitatii prin atribute si masurare). Cu cat curba
operativa aleasa este situata mai spre stanga, cu atat controlul este mai sever.
4.5.2. Continutul planului de verificare
Planul de verificare trebuie sa includa urmatorii parametri,
indiferent de tipul caracteristicilor (masurabile sau atributive):
nivelul de calitate acceptabil - AQL;
nivelul de verificare - Nv;
tipul de esantionare;
gradul de severitate.
Nivelurile AQL si de
verificare Nv trebuie sa fie precizate obligatoriu in
contractul furnizor-client.
(1) Nivelul de calitate acceptabil AQL este o problema
contractuala furnizor-client. El se exprima in procente cuprinse
intre 0,01 si 10% conform tabelului 4.7:
Daca la un
produs se controleaza mai multe
caracteristici de calitate se poate proceda in mai multe moduri:
|
La cresterea fractiunii
defective, scade probabilitatea de acceptare
Patru puncte caracteristice
1. Probabilitate maxima de
acceptare
2. Probabilitate minima
de acceptare
3. Riscul furnizorului
4. Riscul clientului
Curba operativa
ideala
Familie de curbe operative
Elementele planului de
verificare
Tabelul 4.7.
Nivelurile AQL

|
|
Acelasi AQL pentru
caracteristici cu aceeasi importanta
Doua AQL pentru
neconformitati minore
si majore
Aplicare
Mai multe AQL in
functie de importanta neconformitatii
Tabelul 4.8.
Valori AQL in cazul unui autoturism
Determina
marimea esantionului
Niveluri
uzuale
daca
riscul si timpi de control sunt medii
Niveluri
speciale
daca
riscul si timpii de control sunt mari
|
Cazul 1: daca toate
caracteristicile controlate au aceeasi
importanta, se acorda aceeasi
valoare AQL tuturor caracteristicilor rezultand un singur plan
de verificare;
Cazul 2: daca unele
caracteristicile controlate au importanta
diferita, se acorda valori
diferite AQL:
□ daca unele dintre
caracteristici conduc la neconformitati
majore, acestea primesc valoare
mica AQL;
□ daca alte caracteristici
conduc la neconformitati
minore, acestea primesc valoare
mare AQL.
Mod de operare: se utilizeaza doua planuri
de verificare si lotul va fi acceptat
daca el corespunde in cazul ambelor planuri de verificare si respins daca dupa unul dintre
planuri sau dupa ambele este necorespunzator;
Cazul 3 daca produsele au importanta foarte
ridicata, se poate apela la mai
multe valori AQL in functie de
importanta neconformitatii asa cum este prezentat in
tabelul 4.8. Se
utilizeaza mai multe planuri de verificare cate valori AQL s-au
atribuit.
|
Caracteristica
|
Definirea caracteristicii
|
AQL
|
|
Critica 1
|
Pericliteaza viata soferului si a
pietonilor
|
|
|
Critica 2
|
Poate face inutilizabil autoturismul
|
|
|
Majora 1
|
Determina performantele
|
|
|
Majora 2
|
Determina fiabilitatea
|
|
|
Minora 1
|
Referitoare la confort si
aspect
|
|
|
Minora 2
|
Referitoare la unele asamblari
si acoperiri mai putin sesizabile
|
|
(2) Nivelul de verificare - Nv Cu ajutorul acestui parametru, se stabileste
marimea esantionului. El depinde
de importanta caracteristicii sau produsului controlat, metoda de control aplicata
si timpul de control necesar.
Se
utilizeaza doua categorii de niveluri de control: (a) uzuale
si (b) speciale:
(a) Nivelurile de verificare
uzuale se folosesc pentru caracteristici si produse obisnuite,
care necesita timpi de control
normali si care au mai fost controlate anterior.
Exista
trei niveluri uzuale aplicabile in
urmatoarele cazuri:
NvI -
atunci cand informatia necesara
nu trebuie sa fie foarte
certa;
NvII -
nivelul aplicat cel mai frecvent, in circa 70% din cazuri;
NvIII -
cand informatia trebuie
sa aiba un grad mai mare de
certitudine.
(b) Nivelurile de verificare speciale
(S1, S2, S3, S4) se
aplica cand nu pot fi controlate
decat esantioane reduse
si riscurile tolerabile sunt
foarte mari, timpul de verificare
este mare sau la care tipul
produselor si caracteristicilor impun un control distructiv (exemplu
industria auto).
Exemplul 1: Pentru un lot
de produse N=1201 . 3200 de
bucati, in functie de nivelul de verificare (Nv), marimea esantioanelor
stabilite este aceea precizata in tabelul
urmator:
|
|
Nv
|
NvIII
|
NvII
|
NvI
|
S1
|
S2
|
S3
|
S4
|
|
N [buc
|
|
|
|
|
|
|
|
Exemplul 2: In
cazul unui lot de 2000 de autoturisme, se pot aplica urmatoarele
niveluri de verificare:
pentru sistemele de directie si franare - NvIII;
pentru consumul de
combustibil - S2;
pentru rezistenta la
soc - S4.
(3) Tipul de
esantionare Se utilizeaza trei tipuri de esantionare: (a) simpla, (b) dubla si (c) multipla.
(a) Esantionarea simpla: Dintr-un lot de marime N,
se extrage aleatoriu, esantionul cu efectivul n care se
controleaza conform schemei din fig. 4.4:
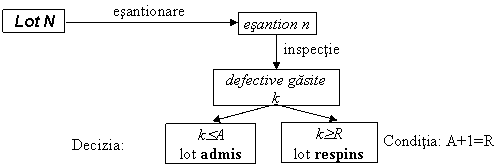
unde:
A
este numarul de acceptare - numarul maxim de
defective gasite in esantion care poate permite acceptarea lotului;
R
- numarul de respingerere - numarul minim de defective
gasite in esantion care determina respingerea lotului.
Esantionarea simpla se aplica in cazul caracteristicilor masurabile sau
in cazul caracteristicilor exprimate prin
atribute daca furnizorii sunt
instabili sau necunoscuti.
(b) Esantionarea dubla:
Se efectueaza prin prelevarea a doua esantioane (n1
si n2) conform schemei din fig. 4.5.




|
Exemplu de niveluri de verificare
- caracteristici foarte importante;
- timpi relativ mici de control
- timp mare de control
- control distructiv.
Tipuri de esantionare
Fig. 4.4.
Esantionarea simpla
Aplicabilitate
Fig. 4.5. Esantionarea dubla
|
|
Fig. 4.6.
Esantionarea multipla
Comparatie intre tipurile de
esantionari
Aplicabilitatea esantionarii duble si
multiple
Stabileste n, A, R
|
(c) Esantionarea multipla: Se realizeaza prelevand succesiv sapte esantioane conform
fig. 4.6. Controlul se bazeaza pe schema de la esantionarea
dubla.
Observatie: Efectivele esantioanelor sunt mai mici decat la
esantionarile precedente, intre ele existand relatiile
n1 n2 n7'< n1 =
n2 < n < n1 n2<n1 n2 n7
Exemplu: Pentru
un lot N = 1201 . 3200 de
bucati, efectivele esantioanelor sunt urmatoarele:
n n1 = n2 n1 n2 n7
n1 n2 n7 > n1 n2 = 160 > n
Esantionarea
dubla si multipla este
aplicabila in cazul produselor (producatorilor) de calitate foarte ridicata sau foarte
redusa, controlandu-se in mod avantajos un esantion redus.
Gradul de severitate: Cu
ajutorul acestui parametru, se stabileste marimea esantionului
si conditia de acceptare a loturilor - numerele de acceptare (A)
si respingere (R) - avand in vedere urmatorii factori: stabilitatea procesului, rezultatele controalelor anterioare
si seriozitatea furnizorilor.
Se folosesc trei grade de severitate: (a) normal, (b) sever, (c) redus.
|
|
(a) Gradul normal se aplica
la controalele unor loturi intamplatoare sau atunci cand se
controleaza pentru prima data un produs.
(b) Gradul sever (mai
pretentios decat cel normal) se caracterizeaza prin numere de
acceptare si respingere mai mici decat acelea de la gradul normal,
pentru acelasi efectiv al esantionului ns:
ns=nn As<An si Rs<Rn
(4.35)
(c) Gradul redus (mai
ingaduitor decat cel normal) are valori mai reduse (proportional)
decat gradul normal pentru efectivul esantionului si numerele de
acceptare si respingere:
nr<nn Ar<An si Rr<Rn
(4.36)
Reguli
de aplicare:
La primul control, se aplica gradul normal;
Dupa primele 10 controale cu grad normal la care loturile au fost admise, se considera
procesul stabilizat si se
trece la gradul redus;
Daca se aplica gradul redus, dar apare o respingere, se
revine la gradul normal;
Daca se aplica gradul normal si din 5 loturi de produse, 2 sunt respinse, se trece la gradul sever;
Daca se aplica gradul sever si sunt admise 5 loturi consecutive, se revine la gradul normal;
Daca se aplica gradul sever si din 10 loturi consecutive mai putin de 5 sunt admise, procesul este considerat total instabil
si verificarea este oprita.
Metoda zero acceptare A=0 Principiul de
baza al metodei este: loturile se admit daca esantionul are
zero defective (produse neconforme).
Metoda se bazeaza pe conceptul "zero
defecte"
elaborat de Philip Crosby care considera ca nu se poate opera cu
niveluri acceptabile ale calitatii, pornind de la premisa
falsa ca neconformitatile sunt inevitabile. Esenta
conceptului este: totul trebuie facut bine de prima data si
de fiecare data.
Caracteristicile metodei sunt:
controlul este mai sever decat cel
obisnuit; nu se accepta loturi cu defective in esantion;
in planul de verificare exista o
singura valoare AQL;
esantionul
este mai mic decat la controlul statistic clasic;
protejeaza mai bine clientul
(controlul clasic apara mai bine furnizorul).
Exista critici al principiului "zero
neconformitati" care sustinand ca principalul vinovat
pentru noncalitate este personalul de executie, considera ca
aplicarea sa este inumana - se ia individului dreptul de a gresi.
In realitate, problemele de fond nerezolvate care conduc la nivelul
scazut al calitatii isi afla rezolvarea in sfera managementului. Datorita avantajelor
sale, metoda este acceptata de Departamentul de stat al S.U.A. In
Romania, a fost oficializata prin STAS 12890 - 90.
|
Mod de aplicare
Tema: de
construit schema logica a regulilor de aplicare
Expresie a conceptului de
excelenta
'doing it right the first time' (DIRTFT).
Calitatea scazuta -
management necorespunzator
|
| | | |
 .com .com |
Copyright ©
2025 - Toate drepturile rezervate.
Toate documentele au caracter informativ cu scop educational. |
|
