
Algoritm pentru aflarea coeficientilor unui polinom atunci cand se cunosc radacinile polinomului
Se dau n numere reale x![]() , x
, x![]() , , x
, , x![]() , n
, n![]() . Vom construi un polinom f care are ca radacini
numerele x
. Vom construi un polinom f care are ca radacini
numerele x![]() , x
, x![]() , , x
, , x![]() .
.
In mod evident, putem aplica relatiile lui Viete, dar va propunem urmatorul algoritm:
Vom considera coeficientul dominant al polinomului ca fiind egal cu 1, de aceea vom lua urmatoarea secventa:
|
|
Plasam prima radacina pe linia urmatoare, in stanga si coboram numarul 1. In continuare vom aplica urmatorul calcul: din valoarea aflata in casuta superioara se scade produsul dintre radacina si valoarea din locatia aflata in stanga casutei superioare, conform schemei:
|
a |
b |
|||
|
x |
b - a x |
In cazul nostru se
obtine:![]()
|
- x |
Pe aceeasi linie se adauga o noua casuta, careia i se atribuie valoarea 0 si se completeaza o noua linie, folosind aceeasi regula de calcul:
|
x |
- x | ||
|
x |
- x |
x |
Procedeul continua similar:
|
x |
- x | |||
|
x |
- x |
x | ||
|
x |
- x |
x |
- x |
pana la
radacina x![]() :
:
|
x |
- x | |||||
|
x |
- x |
x | ||||
|
|
|
|
|
|
| |
|
x |
- x |
x |
- x |
(- 1)
x |
Se observa ca
ultima linie din schema algoritmului contine exact coeficientii
polinomului ce are ca radacini numerele x![]() , x
, x![]() , , x
, , x![]() .
.
Ideea algoritmului se
bazeaza pe urmatoarea recurenta: daca f = X![]() + a
+ a![]() X
X![]() + + a
+ + a![]() este polinomul de coeficient dominant 1, care are
radacinile x
este polinomul de coeficient dominant 1, care are
radacinile x![]() , x
, x![]() , , x
, , x![]() atunci g = (X
atunci g = (X![]() + a
+ a![]() X
X![]() + + a
+ + a![]() )(X - x
)(X - x![]() ) este polinomul cu radacinile x
) este polinomul cu radacinile x![]() , x
, x![]() , , x
, , x![]() .
.
Dintr-un calcul simplu
g = X![]() - x
- x![]() X
X![]() + a
+ a![]() X
X![]() - a
- a![]() x
x![]() X
X![]() + a
+ a![]() X
X![]() + + a
+ + a![]() X - a
X - a![]() x
x![]() ,
,
de unde g = X![]() + (a
+ (a![]() - x
- x![]() )X
)X![]() + (a
+ (a![]() - a
- a![]() x
x![]() )X
)X![]() + - a
+ - a![]() x
x![]() .
.
Daca scriem g = X![]() + b
+ b![]() X
X![]() + b
+ b![]() X
X![]() + +b
+ +b![]() X + b
X + b![]() si identificam coeficientii, se obtine:
si identificam coeficientii, se obtine:
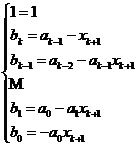
Dupa cum se observa, este vorba de calculul pe care l-am folosit in algoritm.
Pentru o mai buna intelegere a algoritmului, sa facem urmatorul exemplu:
Consideram numerele -1, 2, 2, 3 si aplicam algoritmul, obtinand:
|
| |||||
Polinomul este f = X![]() - 6X
- 6X ![]() + 9X
+ 9X![]() + 4X - 12.
+ 4X - 12.
Problema aflarii coeficientilor unui polinom atunci cand se cunosc radacinile poate fi tradusa in limbajul informaticii astfel:
Fiind
date numerele x![]() , x
, x![]() , , x
, , x![]() , n
, n![]() fixat, sa se afle un polinom care are ca radacini
aceste numere, folosind un singur vector.
fixat, sa se afle un polinom care are ca radacini
aceste numere, folosind un singur vector.
Rezolvare:
Deoarece polinomul are n
radacini, rezulta care are gradul n si prin urmare are n +
1 coeficienti. De aceea vom considera un vector v de lungime n + 1 in care
stocam valoarea 1 in prima locatie si x![]() , x
, x![]() , , x
, , x![]() in urmatoarele n locatii.
in urmatoarele n locatii.
Notam acest vector
v = (v![]() , v
, v![]() , , v
, , v![]() ).
).
|
v |
v |
v |
v |
|
v |
|
x |
x |
x |
|
x |
Singurul lucru de care
mai avem nevoie este o locatie de memorie m, in care, pentru inceput,
stocam valoarea x![]() , inlocuind-o in vectorul v cu 0:
, inlocuind-o in vectorul v cu 0:
|
m |
v |
v |
v |
v |
|
v |
|
|
x |
x |
x |
|
x |
Acum aplicam
calculul expus in prezentarea algoritmului: in locatia v![]() plasam rezultatul v
plasam rezultatul v![]() - mv
- mv![]() . Obtinem:
. Obtinem:
|
v |
v |
v |
v |
v |
|
|
- x |
x |
x |
|
x |
Stocam acum
valoarea x![]() in locatia m, inlocuind pe x
in locatia m, inlocuind pe x![]() cu 0:
cu 0:
|
m |
v |
v |
v |
v |
|
v |
|
|
x |
- x |
x |
|
x |
Pentru ca in
calculul nostru avem nevoie de valoarea din locatia anterioara, vom
calcula mai intai valoarea v![]() care este egala cu 0 - x
care este egala cu 0 - x![]() = x
= x![]() x
x![]() si apoi valoarea v
si apoi valoarea v![]() care e egala cu - x - 1
care e egala cu - x - 1![]() x
x![]() = - x
= - x![]() - x
- x![]() .
.
|
v |
v |
v |
v |
v |
|
|
- x |
x |
x |
x |
Din acelasi motiv,
la fiecare pas componentele vectorului v se calculeaza dinspre v![]() spre v
spre v![]() .
.
In final vectorul v va stoca exact coeficientii polinomului cautat.
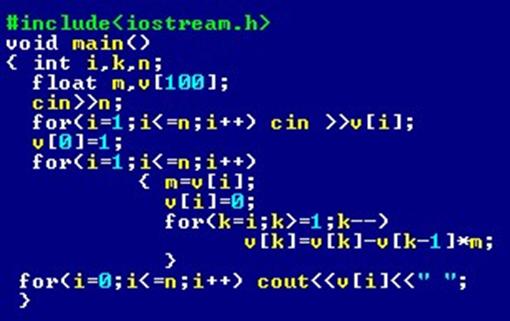
In limbajul C++ algoritmul poate fi traspus astfel:
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |