
Automatele de ordinul 2. Automatele elementare - Circuitul basculant bistabil de tip T
Structurile logice ce implementeaza automatele de ordinul 2 se caracterizeaza printr-o autonomie partiala, la limita totala, in raport cu evolutia intrarilor. O secventa binara aplicata la intrarea unei astfel de structuri va genera la iesire un raspuns partial dependent de aceasta si puternic influentat de secventele anterioare prin "starea" in care s-a aflat structura logica la inceputul secventei. La aceste circuite in paralel cu evolutia iesirilor are loc si o evolutie in spatiul starilor ce confera circuitelor autonomie sporita.
Structurari ulterioare vor oferi proprietati mai complexe sistemelor numerice, dar toate vor fi marcate de autonomia conferita de evolutia in spatiul starilor.
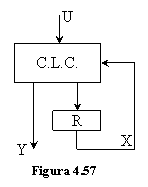 Schema
de principiu cea mai simpla a unui automat de ordinul doi, numit si
automat elementar, este data in fig.4.57 in care:
Schema
de principiu cea mai simpla a unui automat de ordinul doi, numit si
automat elementar, este data in fig.4.57 in care:
R este un registru, adica un automat de ordinul 1, denumit in mod uzual registru de stare.
CLC este un circuit logic combinational ce calculeaza functiile f si g.
U, Y, X - multimile marimilor de intrare, iesire si stare cu semnificatiile definite in paragraful 4.1.1.
1. Circuitul basculant bistabil de tip T
Structura logica cea mai simpla care materializeaza fizic un automat de ordinul 2 este aceea la care dimensiunile multimilor U, X si Y sunt minime. Intrucat evolutia in spatiul starilor este o caracteristica a automatelor de ordinul 2 rezulta ca multimea X va trebui sa aiba cel putin doua elemente. Multimea U poate avea un singur element sau doua elemente. In primul caz avem insa un generator pur, in timp ce, in al doilea caz, se poate vorbi de un control al evolutiei automatului prin intermediul intrarilor. Indiferent de varianta luata in considerare pentru multimea U, rezulta ca elementele multimilor U si respectiv X pot fi codificate cu ajutorul unei singure variabile binare.
In cazul in care multimea U are un singur element, evolutia in spatiul starilor a automatului considerat va consta intr-o tranzitie continua intre cele doua stari ale multimii X. Daca multimea U are insa doua elemente este posibila si blocarea procesului de tranzitie intr-una din cele doua stari.
Observatie:
pentru a simplifica si mai mult structura din fig.4.57 vom considera
ca informatia de la iesirea automatului se refera
nemijlocit la starea sa, deci ![]() .
.
In continuare vom considera cele doua situatii disitincte in care multimea U are unul sau doua elemente:
in cazul in care U are un singur element el poate fi
codificat cu o ![]() si
si ![]() cele doua elemente ale multimii X ce
vor fi codificate cu variabila de stare x
prin adoptarea conventiei ca x=0
cand automatul este in starea
cele doua elemente ale multimii X ce
vor fi codificate cu variabila de stare x
prin adoptarea conventiei ca x=0
cand automatul este in starea ![]() si respectiv x=1 cand automatul este in starea
si respectiv x=1 cand automatul este in starea ![]() . Schema logica
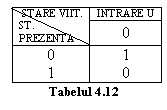
si tabelul tranzitiilor pentru un automat astfel definit sunt redate
in fig.4.58 si tab.4.12. In
aceasta structura circuitul inversor implementeaza circuitul
logic combinational din fig.4.57, iar bistabilul D indeplineste
functia unui registru pe un bit.
. Schema logica
si tabelul tranzitiilor pentru un automat astfel definit sunt redate
in fig.4.58 si tab.4.12. In
aceasta structura circuitul inversor implementeaza circuitul
logic combinational din fig.4.57, iar bistabilul D indeplineste
functia unui registru pe un bit.
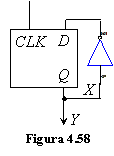
in cazul in
care multimea U are doua elemente ![]() si
si ![]() ele pot fi codificate cu o singura
variabila u care este u=0 cand
ele pot fi codificate cu o singura
variabila u care este u=0 cand ![]() este activa si u=1 cand
este activa si u=1 cand ![]() este activa. Cele doua stari se
codifica ca si in cazul precedent. In functie de circuitele
utilizate pentru implementarea circuitului logic combinational din
fig.4.57 se pot obtine diverse structuri. Trei posibile structuri de
ordinul doi si tabelele tranzitiilor ce le
corespund sunt prezentate in fig.4.59, 4.60, 4.61 si respectiv tab.4.13,
4.14, 4.15.
este activa. Cele doua stari se
codifica ca si in cazul precedent. In functie de circuitele
utilizate pentru implementarea circuitului logic combinational din
fig.4.57 se pot obtine diverse structuri. Trei posibile structuri de
ordinul doi si tabelele tranzitiilor ce le
corespund sunt prezentate in fig.4.59, 4.60, 4.61 si respectiv tab.4.13,
4.14, 4.15.
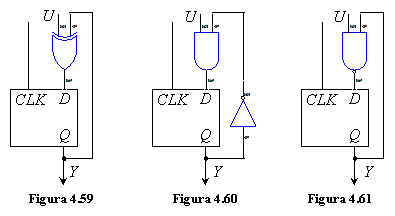
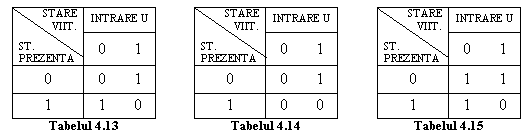

Structura din fig.4.59 este cunoscuta sub denumirea de circuit basculant bistabil de tip T simbolul sau fiind redat in fig. 4.62. Din tabelul tranzitiilor acestui bistabil se observa ca daca la intrarea T se aplica semnal logic 1 atunci el isi schimba starea la fiecare impuls de tact. Dimpotriva, daca la intrarea T se aplica semnal logic 0 starea bistabilului si deci iesirea sa, raman neschimbate. Rezulta deci ca functionarea bistabilului depinde de starea sa intrucat, de exemplu, ca sa treaca in starea complementara el trebuie sa-si cunoasca starea prezenta, adica starea in care se afla.
Structura din fig.4.58 poate fi considerata un bistabil T permanent activat.
2. Circuitul basculant bistabil JK
Bistabilul de tip D, utilizat ca element de memorare pentru CBB de tip T, constituie solutia pentru rezolvarea nedeterminarii care apare in functionarea CBB de tip RS (ce functioneaza dupa principiul master-slave) atunci cand R=S=1.
Structura RS poate fi reluata si prin introducerea unei reactii de tipul celei din fig.4.57 se obtine un circuit basculant bistabil cu doua intrari care vor accepta toate combinatiile posibile de valori. Fiind vorba de un bistabil (cu doua stari distincte) si doua intrari ce se modifica independent, s-au impus patru moduri de functionare distincte si anume: la cele trei moduri specifice automatului RS (nu modifica starea, tranzitie in starea zero si tranzitie in starea 1) s-a adaugat modul de functionare specific bistabilului de tip T, si anume, tranzitia in starea complementara.
ST.PREZ. ST.VIIT. 0 0 0 1 0 1 0 1 1 1 Tabelul 4.17 J K R S 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 1 0 1 0 1 0 0 1 0 1 1 0 1 1 0 0 1 1 0 1 0 1 1 1 1 0 1 0 Tabelul 4.18 J K 0 0 0 0 1 1 1 0 1 1 1 0 Tabelul 4.19
J
K
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
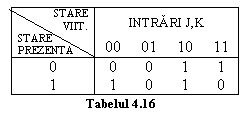
Bistabilul obtinut va fi caracterizat prin
doua stari interne 0 si 1 si prin cele patru
combinatii posibile ale celor doua intrari care poarta
denumirea de intrari J si K. Structura acestui bistabil este
prezentata in fig.4.63, iar functionarea sa este redata in
tabelul tranzitiilor 4.16. O reprezentare mai frecvent intalnita a
acestui tabel este cea din tab.4.17. Tinand cont
de faptul ca starea ![]() poate fi 0 sau 1 acest tabel a fost detaliat
sub forma 4.18.
poate fi 0 sau 1 acest tabel a fost detaliat
sub forma 4.18.
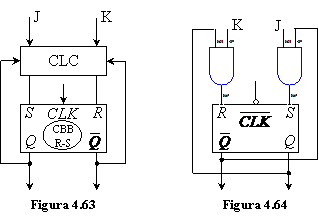
In tabelul 4.18 au fost specificate si semnalele logice pe care trebuie sa le aiba asigurate intrarile R si S din fig.4.63 astfel ca functionarea sa fie conforma celei definite pentru CBB de tip JK. Rezulta urmatoarele functii
![]() ;
; ![]()
ce trebuiesc implementate de circuitul logic combinational din fig.4.63 (fig.4.64). De mentionat ca realizarea practica a CBB de tip JK implica unele modificari in raport cu schema principiala din fig.4.64, modificari menite sa-i sporeasca performantele functionale.
Un tabel frecvent utilizat in cazul implementarii circuitelor secventiale cu bistabile JK este tabelul excitatiilor bistabilului JK care, pornind de la schema logica a acestui bistabil (fig.4.64), stabileste valorile logice ce trebuiesc aplicate la cele doua intrari J si K astfel ca tranzitia de stare sa fie cea dorita (tab.4.19).
Modul de reprezentare a unui CBB de tip JK este cel din fig.4.65.
3. Numaratoare
Aplicatia principala a circuitelor basculante bistabile o constituie circuitele numaratoare. Din analiza schemei din fig.4.59 se observa ca la fiecare impuls de tact continutul bistabilului D este rezultatul unei sume modulo 2 cu intrarea prin circuitul SAU-EXCLUSIV, adica daca intrarea U=0 starea bistabilului nu se modifica, iar daca U=1 avem o modificare de tip modulo 2. Capacitatea de numarare este limitata la 2 datorita faptului ca bistabilul are numai doua stari distincte. Rezulta prin urmare ca un CBB de tip T este un circuit de numarare binara comandat prin T=1. Pentru sporirea capacitatii de numarare se interconecteaza mai multe bistabile de tip T. In functie de acest mod de conectare se definesc doua mari categorii de numaratoare:
a) Numaratoare asincrone, la care impulsul de tact nu se aplica la acelasi moment de timp la toate automatele elementare independente de tip T, la intrarile carora se aplica constanta logica 1.
b) Numaratoare sincrone, caracterizate prin faptul ca impulsurile de tact sunt aplicate simultan tuturor bistabilelor, iar intrarile de tip T pot lua doua valori logice in functie de tranzitia realizata.
In ambele cazuri numaratorul se obtine prin interconectarea unor automate de ordinul 2 in asa fel incat sa nu se introduca o reactie suplimentara.
Exista si posibilitatea utilizarii bistabilelor de tip D, care sunt automate de ordinul 1, dar in acest caz numaratorul nu mai este o "colectie" de automate elementare interconectate, ci un automat complex cu o bucla globala introdusa peste un sistem de ordinul 1 (bistabilul D). Rezulta ca si in acest caz numaratorul este tot un automat de ordinul 2.
3.1. Numaratoare asincrone
Numaratorul asincron este tipul de numarator elementar realizat in mod uzual sub forma de circuit integrat. Dintre toate numaratoarele el are logica de functionare cea mai simpla si este cel mai usor de proiectat, dar este totusi limitat in ceea ce priveste viteza de lucru.
Avand in vedere faptul ca un asemenea circuit trebuie sa functioneze conform secventei de numarare a numerelor binare rezulta ca principiile sale de functionare pot fi concluzionate din observarea acestei secvente. Fie secventa de numarare a primelor 16 numere binare:
abcd
 0000 0110 1011
0000 0110 1011
0001 0111 1100
0010 1000 1101
0011 1001 1110
0100 1010 1111
0101
In urma analizarii ei se pot desprinde doua concluzii:
1) valoarea celui mai putin semnificativ bit, pentru noi -d, comuta la cresterea cu o unitate a oricarui numar;
2) valoarea celorlalti biti comuta ca o consecinta a tranzitiei din 1 in 0 a bitului de rang imediat inferior.
Daca vom asocia fiecarui bit un circuit basculant bistabil T (cu T=1) ce comuta pe frontul negativ al impulsului de tact si vom conecta iesirea fiecarui bistabil la intrarea de tact a bistabilului urmator, atunci aplicand impulsurile de tact bistabilului asociat celui mai putin semnificativ bit, acesta va comuta la fiecare impuls. La fiecare comutare din 1 in 0 a acestui circuit basculant bistabil frontul negativ al acestei tranzitii va provoca comutarea circuitului bistabil de ordin imediat superior respectand astfel concluzia nr.2. Acelasi fenomen va avea loc si la tranzitiile din 1 in 0 ale celorlalte circuite basculante bistabile putandu-se obtine astfel, prin conectarea in cascada a n bistabile, un numarator pe n biti.
In fig.4.66 este prezentata schema unui numarator asincron pe 4 biti, iar in fig.4.67 diagrama de timp asociata lui (neglijand intarzierile introduse de comutarea circuitelor).
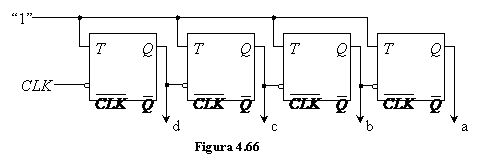
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 CLK d c b a Figura 4.67
Initial
bistabilele sunt aduse in starea 0 de catre impulsul de tact cu
numarul de ordine 0 (adica ![]() ).
Aplicarea impulsului de tact cu numarul de ordine 1 va
provoca comutarea primului bistabil (
).
Aplicarea impulsului de tact cu numarul de ordine 1 va
provoca comutarea primului bistabil (![]() ) celelalte
ramanand nemodificate intrucat, asa cum de fapt s-a precizat deja, ele
comuta pe frontul descrescator al impulsurilor de tact. Cel de-al
doilea impuls de tact va provoca comutarea lui
) celelalte
ramanand nemodificate intrucat, asa cum de fapt s-a precizat deja, ele
comuta pe frontul descrescator al impulsurilor de tact. Cel de-al
doilea impuls de tact va provoca comutarea lui ![]() din 1 in 0
ceea ce va crea conditia necesara comutarii valorii lui
din 1 in 0
ceea ce va crea conditia necesara comutarii valorii lui ![]() din 0 in
1. Inaintea aplicarii impulsurilor de tact cu
numarul de ordine 16 toate bistabilele vor fi in starea 1. Acest
impuls, al 16-lea, va determina trecerea lor in starea
0. Rezulta deci ca starile numaratorului din
figura se vor repeta dupa
din 0 in
1. Inaintea aplicarii impulsurilor de tact cu
numarul de ordine 16 toate bistabilele vor fi in starea 1. Acest
impuls, al 16-lea, va determina trecerea lor in starea
0. Rezulta deci ca starile numaratorului din
figura se vor repeta dupa ![]() impulsuri si
ca in general repetarea se va face dupa
impulsuri si
ca in general repetarea se va face dupa ![]() impulsuri
de tact, n fiind un numar egal
cu numarul bistabilelor utilizate la implementare.
impulsuri
de tact, n fiind un numar egal
cu numarul bistabilelor utilizate la implementare.
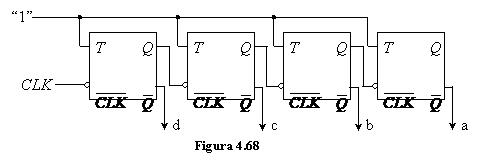 Din
studiul formelor de unda din fig.4.67 se mai poate observa ca un astfel de numarator functioneaza
si ca un divizor de frecventa. Daca vom considera ca
semnalul de tact (CLK) are frecventa f,
atunci semnalul d are frecventa
Din
studiul formelor de unda din fig.4.67 se mai poate observa ca un astfel de numarator functioneaza
si ca un divizor de frecventa. Daca vom considera ca
semnalul de tact (CLK) are frecventa f,
atunci semnalul d are frecventa ![]() , c are frecventa
, c are frecventa ![]() , etc.
, etc.
Cu ajutorul unei scheme asemanatoare cu cea precedenta (fig.4.68) se poate implementa un numarator asincron invers (primul poarta si denumirea de numarator asincron direct) care va genera numerele binare din secventa de numarare in ordine inversa.
Caracterul asincron al acestor numaratoare se datoreste faptului ca, exceptand bistabilul asociat celui mai putin semnificativ bit, celelalte bistabile nu comuta sincron, ci ca o consecinta a comutarii bistabilului de ordin imediat inferior. Deci in cazul in care tranzitia din secventa de numarare implica modificarea valorii a mai multor biti, starea finala corecta nu se stabileste sincron, ci prin comutarea succesiva a 2 pana la n bistabile. Timpul de comutare deci a unui numarator asincron este, in cel mai defavorabil caz, egal cu suma timpilor de comutare a tuturor bistabilelor din structura sa. Aceasta este deficienta principala a numaratoarelor asincrone, deficienta eliminata in cazul numaratoarelor sincrone cu pretul adaugarii unor circuite combinationale suplimentare.
Avantajul principal al acestor numaratoare consta in simplitatea schemei ce se obtine prin interconectarea directa a bistabilelor ce le compun.
3.2. Numaratoare sincrone
Se caracterizeaza prin faptul ca semnalul de sincronizare se aplica simultan la intrarea tuturor bistabilelor din structura, bascularea sau nebascularea unui bistabil fiind conditionata prin intermediul semnalului ce se aplica la intrarea T, rezulta la intrarea fiecarui T va trebui sa avem o structura combinationala ce sa decida situatiile in care bistabilul respectiv isi va modifica starea la aparitia proximului impuls de sincronizare. Structurile logice combinationale vor genera conditiile de tranzitie inaintea aplicarii impulsului de sincronizare.
Avand in vedere acest mod de aplicare a structurii combinationale va trebui analizata secventa de numarare binara.

Figura 4.69
In urma analizarii secventei de numarare binara se ajunge la ecuatiile 4.2:
![]()
![]()
![]()
![]()
![]()
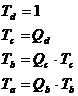 (4.2)
(4.2)
Structura care se obtine pentru numarator este cea din figura 4.70
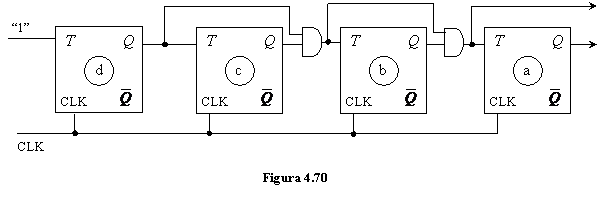
De
remarcat ca pe langa cele doua intrari J si K, numite
intrari sincrone, unele bistabile materializate fizic mai au
prevazute si intrarile asincrone ![]() si
si ![]() . Din
punct de vedere functional intrarile asincrone sunt prioritare in
raport cu cele sincrone.
. Din
punct de vedere functional intrarile asincrone sunt prioritare in
raport cu cele sincrone.
Observatie: (a) Daca se impune conditia J=K, adica se leaga impreuna cele doua intrari, se obtine un bistabil de tip T. Familiile uzuale de circuite integrate nu contin bistabile de tip T, dar acestea pot fi realizate cu bistabile JK.
(b)
Daca se conecteaza un inversor intre cele
doua intrari astfel ca ![]() se obtine din punct de vedere
functional un bistabil de tip D.
se obtine din punct de vedere
functional un bistabil de tip D.
Rezumat
In prima parte a capitolului
privitor la sistemele digitale facem o prezentare a catorva notiuni cu
privire la automatelor cu stari finite, tipuri posibile, moduri de definire
si de reprezentare ale acestora. Concret ne referim la automatele de tip
Mealysi respectiv
Urmeaza o clasificare a automatelor dupa tipul acestora. La fiecare tip de automat (de ordinul 0, 1, etc.) este prezentata o structura a acestuia, posibilitatea de a obtine un automat de un ordin folosind automate de un ordin inferior si sunt date exemple.
Dupa aceasta introducere urmeaza propriu-zis prezentarea circuitelor logice combinationale. Se incepe cu sinteza folosind porti logice NU, SI, SAU continuand cu sinteza folosind porti logice SI-NU respectiv SAU-NU. La aceasta din urma metoda sunt date si exemple de functii implementate.
Circuitul
multiplexor face obiectul paragrafului urmator fiind prezentata
schema bloc a acestuia, tabelul de functionare
si schema desfasurata a acestuia folosind
Alaturi de multiplexor sunt prezentate si circuitele decodificator si demultiplexor. Ele doua circuite sunt prezentate impreuna datorita structurii asemanatoare. La fiecare dintre ele sunt prezentate schema detaliata cu porti logice, schema bloc si tabelele de functionare. Se arata si posibilitatea de a implementa functii logice folosind decodificatoare.
Se trece la memoria fixa ROM cu prezentarea de diverse structuri precum si sinteza folosind memorii ROM. In continuare sunt abordate structurile logice
programabile ca exemplu fiind prezentata implementarea unui convertor din cod zecimal codificat binar in cod Gray folosind aceste circuite.
Ca aplicatii ale circuitelor logice combinationale sunt prezentate semisumatorul, sumatorul (la fiecare cu structura si tabel de functionare. La sumator este construit cel pe un bit dupa care este extins serie la unul pe 4 biti.
Circuitele logice ce implementeaza automate de ordinul 1 se pot clasifica astfel:
- latch-ul care constituie elementul tipic, de baza, pentru implementarea automatului de ordinul 1.
- CBB ce functioneaza dupa principiul master-slave si registrul de deplasare serie ce constituie extensii de tip serie ale elementelor tip;
-memoria RAM care constituie extensie de tip paralel;
- registrul paralel, de stocare, ce constituie o extensie de tipul serie-paralel.
Caracteristica comuna a acestor patru tipuri de structuri este aceea ca poseda capacitatea de stocare a datelor constituind celule de memorie sau retele de celule de memorie.
La nivelul acestor circuite apare o prima forma de manifestare a unei autonomii incipiente in raport cu intrarile ce nu mai determina, decat in anumite conditii, modificarea iesirilor. Aceasta autonomie in raport cu intrarile va creste insa prin introducerea unor noi reactii.
Toate tipurile de circuite logice care implementeaza automate de ordinul 1, se regasesc prezentate ca structura si functionare in cadrul primei parti a prezentului capitol. Sunt prezentate pentru fiecare circuit, pe langa schema bloc, reprezentarea acestuia precum si tabelul (tabelele) de functionare.
Dintre automatele de ordinul 2 sunt prezentate ca posibile structuri : bistabilul T cu posibilitatea de obtinere dintr-un bistabil D si tabel de functionare; bistabilul J-K cu modul de obtinere al acestuia pornind de la un bistabil RS si din nou modurile de functionare.
In finalul capitolului sunt prezentate numaratoarele sincrone si asincrone. Functionarea acestora este explicata folosind diagrame temporale. La fiecare dintre cele doua tipuri de numaratoare sunt prezentate ecuatiile in urma carora se ajunge la respectiva structura precum si schema realizata folosind bistabile T si acolo unde este cazul si porti logice.
Intrebari si probleme
1. Ce intelegeti prin automat de tip Mealy?
2.
Ce intelegeti prin automat de tip
3. Care sunt simbolurile folosite (si ce semnificatii au) la construirea organigramelor functionale?
4. Ce intelegeti prin automat de ordinul 0?Prezentati schema bloc si organigrama functionala.
5. Cum este obtinut automatul de ordinul 1? Dar unul de ordinul 2?
6. Care sunt etapele principale de parcurgere ale sintezei unui circuit combinational?
7. Care sunt etapele principale de parcurgere ale analizei unui circuit combinational?
8. Prezentati modul de obtinere al portilor NU, SI, SAU folosind doar porti SI-NU respectiv SAU-NU.
9. Prezentati schema desfasurata si tabelul de functionare al unui multiplexor cu 8 intrari de date.
10. Cum poate fi obtinut un multiplexor cu 16 intrari de date folosind doua cu 8 intrari de date si porti logice?Dar unul cu 64 de intrari de date folosind doar multiplexoare cu 8 intrari de date?
11. Care este schema desfasurata si tabelul de functionare al unui decodificator?Faceti o comparatie cu un demultiplexor.
12. Cum pot fi folosite multiplexoarele si demultiplexoarele in transmisii de date?
13. Care este schema bloc a unei memorii ROM?
14. Ce intelegeti prin structuri logice programabile? Care sunt avantajele lor?
15. Construiti un sumator pe un bit folosind un multiplexor cu 8 intrari de date. Aceiasi problema folosind un decodificator cu 4 intrari de adresa.
16. Care este diferenta dintre un sumator si un semisumator?
17. Cum poate fi obtinut un sumator pe 4 biti folosind doar sumatoare pe un bit?
18. Prezentati structura si explicati modul de functionare al unui bistabils asincron.
19. Ce imbunatatiri pot fi aduse unui bistabil RS asincron?
20. Prezentati schema bloc precum si modul de functionare al unei memorii RAM.
21. Ce intelegeti prin principiul master- slave?
22. Folosind bistabile D proiectati un registru pe 4 biti deplasare/rotire stanga/dreapta avand si posibilitatea de incarcare paralela.
23. Care este diferenta dintre un registru serie si unul paralel?
24. Prezentati structura registrului serie-paralel si explicati functionarea acestuia.
25. Ce este un circuit basculant bistabil T? Cum functioneaza?
26. Prezentati modul de functionare al unui bistabil JK.
27. Care este difereta dintre un numarator sincron si unul asincron pe 4 biti? Prezentati comparativ cele 2 structuri.
28. Proiectati folosind bistabile JK un numarator sincron modulo 10.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |