
Variabile aleatoare discrete. Legea de distributie a unei variabile aleatoare
Definitia 1: Variabila x luand in urma unei masuratori una din valorile unei suite finite sau infinite x1, x2, xk ,. se numeste variabila aleatoare discreta daca la fiecare valoare xk corespunde o probabilitate pk pentru ca variabila x ia valoarea xk.
Rezulta din definitie ca la fiecare valoare xk ii este asociata o probabilitate pk
Relatia functionala ce leaga probabilitatea pk de xk este numita legea de distributie a probabilitatilor unei variabile aleatoare discrete, sau simplu "legea de distributie" .(vezi tabelul)
Aceeasi lege de distributie poate fi data grafic, sub forma unui poligon de distributie cand se construieste intr-un sistem de coordonate punctele de coordonate (xk , pk) pe care le reunim printr-o linie franta.(vezi fig.)
Legea de distributie poate de asemenea sa fie data sub forma analitica.
Pk = f (xk)
|
Valori posibile ale variabilei aleatoare |
x1 x2 ........ .... xk .... |
|
Probabilitatea acestor valori |
p1 p2 ....... .... pk .... |
(tabel 1)
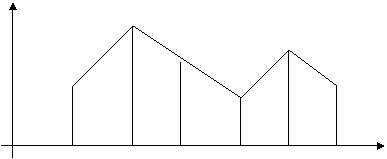
p
(fig. 1)
0 n
Faptul ca variabila aleatoare x va lua cu necesitate una din valorile sumei
x1, x2, . . . xk .
este un eveniment cert astfel ca avem intotdeauna:
![]() = 1 (VII
25)
= 1 (VII
25)
pentru o serie finita, sau:
![]() = 1 (VII
25')
= 1 (VII
25')
pentru o serie infinita.
Exemplul 1: Probabilitatea ca sa
iasa unul din numerele de pe fetele unui zar este ![]()
![]()
![]() x 1 2 3 4 5 6
x 1 2 3 4 5 6
p ![]()
![]()
![]()
![]()
![]()
![]()
Exemplul 1: Fie p probabilitatea de realizare a evenimentului A in cursul fiecarei probe in parte dintr-o serie infinita de probe. Variabila aleatoare x este numarul de ordine al experientei in cursul careia evenimentul A se realizeaza pentru prima data . Sa se gaseasca legea de distributie a variabilei aleatoare x.
Solutie:![]() Variabila aleatoare x poate sa ia oricare
valoare 1,2,3. Probabilitatea p1
pentru ca evenimentul A sa fie
realizat in cursul unei probe va fi:
Variabila aleatoare x poate sa ia oricare
valoare 1,2,3. Probabilitatea p1
pentru ca evenimentul A sa fie
realizat in cursul unei probe va fi:
P1 = P(A) = p
Probabilitatea p2 pentru ca evenimentul A sa nu fie realizat in cursul primei probe si sa se realizeze in cea de-a doua este:
P2 = P(![]() si A) = (1-p) p
si A) = (1-p) p
Probabilitatea p3 pentru ca evenimentul A sa nu fie realizat nici in prima proba si nici in cea de-a doua proba, ci numai in a treia va fi:
P3 = P(![]() si
si![]() si A) = (1-p) (1-p) p = (1-p)2 p
si A) = (1-p) (1-p) p = (1-p)2 p
si asa mai departe:
pk = (1-p)k-1p (VII 26)
Tabloul de distributie va fi:
![]() x 1 2 3 ..... k ...
x 1 2 3 ..... k ...
![]() pk p (1-p)p (1-p)2p .... (1-p)k-1
p ....
pk p (1-p)p (1-p)2p .... (1-p)k-1
p ....
Avem deci si:
![]()
![]()
![]() = 1
= 1
deoarece ![]() este o serie geometrica cu ratia (1-p)
este o serie geometrica cu ratia (1-p)
Problema studiata mai sus se aplica problemei tirului pana cand primul foc va lovi tinta.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |