Puterea unui punct fata de un cerc
Aceasta nota aduce in atentie chestiuni geometrice deloc noi,dar care adunate cu grija poate ca aduc un mic ajutor celor care se pregatesc pentru diverse concursuri scolare si un pic de bucurie tuturor celor care nu au uitat frumusetea geometriei sintetice la ale carei nestemate , prea usor parca , am renuntat in matematica de liceu.
Teorema
: Daca ![]() sunt patru puncte distincte situate pe un cerc
sunt patru puncte distincte situate pe un cerc ![]() astfel incat
astfel incat ![]() ,atunci
,atunci ![]() .
.
Demonstratie : Evident , deosebim cazurile :
1) ![]()
![]()
|
Deoarece (opuse la
varf),deducem Observatie:E util sa |
C B A |
reformulam:
daca ![]()
![]() atunci pentru orice coarda
atunci pentru orice coarda ![]() care contine punctul M
, produsul
care contine punctul M
, produsul ![]() este constant.Valoarea constanta a acestui produs
inmultita cu
este constant.Valoarea constanta a acestui produs
inmultita cu ![]() se noteaza cu
se noteaza cu ![]() si se numeste puterea
punctului interior M fata de cercul dat .
si se numeste puterea
punctului interior M fata de cercul dat .
2) ![]()
![]()
|
Din |
M |
Valoarea
constanta a acestui produs se noteaza cu ![]() si se numeste puterea
punctului exterior M fata de cerc.
si se numeste puterea
punctului exterior M fata de cerc.
Daca M este un punct fixat ne propunem acum sa determinam in functie de elemente cunoscute , expresia puterii sale fata de cerc.
1) ![]()
![]()
E suficient sa consideram coarda (AB) ca fiind diametru si deci
![]()
![]()
2) ![]()
![]()
La fel , consideram A , O , M , B coliniare ( in aceasta ordine)
astfel incat (AB) este
diametru si astfel avem : ![]()
![]() .
.
Observatie
: Daca ![]()
![]() ,
, ![]() ,iar daca MT e
tangenta la cerc, punctul T
fiind punctul de tangenta , avem
,iar daca MT e
tangenta la cerc, punctul T
fiind punctul de tangenta , avem ![]() . Asadar pentru orice punct M din planul cercului
. Asadar pentru orice punct M din planul cercului ![]() avem :
avem : ![]()
![]() .
.
În continuare va propunem unele aplicatii ( mai mult sau mai putin cunoscute,unele deosebit de frumoase).
Problema 1 . Daca ![]() si
si ![]() sunt cercul circumscris , respectiv cercul inscris
pentru un triunghi ABC , atunci
sunt cercul circumscris , respectiv cercul inscris
pentru un triunghi ABC , atunci ![]()
Solutie :
|
Notam cu D
intersectia bisectoarei |
A |
![]() , adica triunghiul BID
este isoscel cu
, adica triunghiul BID
este isoscel cu ![]() .
.
Folosind teorema sinusurilor in ![]() avem si
avem si
![]() .
.
Notam acum E
piciorul perpendicularei din I pe CA si avem : ![]() , iar din
, iar din ![]()
( dreptunghic
in E ) , deducem : 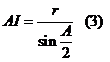 .
.
Este suficient acum
sa scriem puterea punctului I
fata de cercul ![]() si obtinem :
si obtinem : ![]() sau , folosind
relatiile (1) , (2) , (3) ,
sau , folosind
relatiile (1) , (2) , (3) , 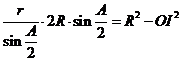 , de unde
, de unde ![]()
( Observatie : ![]() conduce acum la
inegalitatea lui Euler , anume
conduce acum la
inegalitatea lui Euler , anume ![]() . ) ■
. ) ■
Problema 2 Daca ![]() este cercul circumscris triunghiului ABC in care G si H sunt centrul de greutate , respectiv
ortocentrul , iar
este cercul circumscris triunghiului ABC in care G si H sunt centrul de greutate , respectiv
ortocentrul , iar ![]() , atunci :
, atunci : ![]()
Solutie :
|
Daca E este
mijlocul lui (BC) si
|
|
Folosind acum puterea
punctului E fata de cercul ![]() ,avem :
,avem :
![]() ,adica
,adica ![]() si ,
revenind,ajungem la :
si ,
revenind,ajungem la :
![]() . E suficient acum sa folosim un alt rezultat
cunoscut,anume teorema medianei,conform careia avem :
. E suficient acum sa folosim un alt rezultat
cunoscut,anume teorema medianei,conform careia avem :
![]() . Din acest moment urmeaza efectiv calcule
fara nici o dificultate.
. Din acest moment urmeaza efectiv calcule
fara nici o dificultate.
Observatie: Egalitatea
propusa se poate obtine si folosind,de exemplu,
relatia ![]() ( Leibniz )
,adevarata pentru orice punct M din planul triunghiului ABC.E
suficient sa luam
( Leibniz )
,adevarata pentru orice punct M din planul triunghiului ABC.E
suficient sa luam ![]()
Propunere : Daca
tot am vazut cum se calculeaza OI
, OG , incercati sa aratati ( si sa
retineti ) cum se poate ajunge si
![]() ■
■
Problema 3 Se considera doua
puncte fixe A si B pe diametrul unui semicerc , egal departate de
centru , iar M si N doua puncte variabile pe semicerc astfel
incat ![]() Sa se arate
ca produsul
Sa se arate
ca produsul ![]() este constant .
este constant .
(Admitere facultate,1986)
Solutie :
|
Consideram tot
cercul din care provine semicercul dat si notam |
|
Deducem acum ![]() ( coarde egal
departate de centru ) si astfel :
( coarde egal
departate de centru ) si astfel : ![]() Cum
Cum ![]() , ajungem
, ajungem ![]() Puterea
Puterea![]() , adica
, adica
![]() ( constant ) . ■
( constant ) . ■
Problema 4 . Se noteaza cu M , N , P mijloacele laturilor (BC),(CA),respectiv (AB) ale unui triunghi ABC. Dreptele AM , BN , CP intersecteaza cercul circumscris triunghiului ABC in Q , S , respectiv T. Sa se demonstreze inegalitatea :
![]()
(Admitere facultate,1987)
Solutie : Folosind puterea punctelor M , N , P fata
de cerc obtinem : ![]() . Suma din membrul stang al inegalitatii
propuse se poate acum scrie :
. Suma din membrul stang al inegalitatii
propuse se poate acum scrie :
![]()
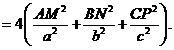 Folosim acum teorema
medianei ,adica
Folosim acum teorema
medianei ,adica
![]() si analoagele
.Urmeaza calcule imediate,grupari convenabile,folosirea in
final a inegalitatilor de tipul
si analoagele
.Urmeaza calcule imediate,grupari convenabile,folosirea in
final a inegalitatilor de tipul ![]() si concluzia
va este la indemana. ■
si concluzia
va este la indemana. ■
Problema 5 . Se considera un cerc
in care este inscris triunghiul isoscel ABC ( ![]() ). Prin A se duce o
coarda care intersecteaza ( BC ) in E si cercul in
F. Sa se arate ca AB este tangenta cercului circumscris triunghiului
BEF .
). Prin A se duce o
coarda care intersecteaza ( BC ) in E si cercul in
F. Sa se arate ca AB este tangenta cercului circumscris triunghiului
BEF .
(Mihail St.Botez)
Solutie : Deoarece ![]() este comun si
este comun si ![]() ( subantind
coarde egale ) deducem ca :
( subantind
coarde egale ) deducem ca : 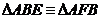 , de unde :
, de unde : ![]() sau
sau ![]() . Folosind puterea
punctului A exterior cercului circumscris triunghiului BEF obtinem ca
AB este tangenta la acest cerc. ■
. Folosind puterea
punctului A exterior cercului circumscris triunghiului BEF obtinem ca
AB este tangenta la acest cerc. ■
Problema 6 . Daca H este ortocentrul
triunghiului ABC si D , E , F sunt picioarele inaltimilor
acestuia ( ![]() ), sa se arate ca :
), sa se arate ca :![]()
Solutie : Puterea punctului H fata de cercul circumscris patrulaterului inscriptibil ABDE
( unghiuri formate de
diagonale cu laturi opuse sunt congruente - sunt chiar unghiuri drepte )
conduce la ![]() . Analog pentru alt
patrulater inscriptibil. ■
. Analog pentru alt
patrulater inscriptibil. ■
Problema 7 . Se considera doua
cercuri ![]() . Sa se determine locul geometric al punctelor din plan
care au puteri egale fata de cele doua cercuri .
. Sa se determine locul geometric al punctelor din plan
care au puteri egale fata de cele doua cercuri .
Solutie : Avem
asadar de gasit multimea punctelor M din plan pentru care ![]() ( # ) .
( # ) .
Fara a
restrange generalitatea problemei putem considera ![]() si notand
si notand ![]() , conditia ( # ) devine
, conditia ( # ) devine ![]() .
.
Avem acum alta problema ( destul de cunoscuta ) : Sa se determine locul geometric al punctelor M din plan pentru care diferenta patratelor distantelor la doua puncte fixe este constanta.
E suficient sa folosim,de exemplu ,
teorema lui Pitagora generalizata in triunghiul ![]() ( sau teorema cosinusului ? ) si obtinem imediat ,
daca N este proiectia lui M pe
( sau teorema cosinusului ? ) si obtinem imediat ,
daca N este proiectia lui M pe ![]() ,ca punctul N este fix , adica locul lui M este o
dreapta perpendiculara pe
,ca punctul N este fix , adica locul lui M este o
dreapta perpendiculara pe ![]() .■
.■
Observatii :
Locul astfel determinat se numeste axa radicala a cercurilor
( si este deci o dreapta perpendiculara pe linia centrelor ) ;
Daca ![]() , atunci axa radicala a cercurilor este chiar dreapta AB
, iar daca MN este tangenta
comuna cercurilor
, atunci axa radicala a cercurilor este chiar dreapta AB
, iar daca MN este tangenta
comuna cercurilor ![]() si
si ![]() , atunci AB intersecteaza (MN) in mijlocul
acestuia .
, atunci AB intersecteaza (MN) in mijlocul
acestuia .
Problema 8 . Se considera un triunghi
ABC si se noteaza cu ![]() mijloacele laturilor
(AC) , respectiv (AB ) , iar cu H piciorul inaltimii din A.
Sa se arate ca cercul circumscris triunghiurilor
mijloacele laturilor
(AC) , respectiv (AB ) , iar cu H piciorul inaltimii din A.
Sa se arate ca cercul circumscris triunghiurilor ![]() si
si ![]() au un punct comun I ,
iar HI intersecteaza
au un punct comun I ,
iar HI intersecteaza ![]() in mijlocul
sau.
in mijlocul
sau.
(Short list,OIM,1970)
Solutie : Consideram D ca fiind al doilea punct de
intersectie a cercurilor circumscrise triunghiurilor ![]() si
si ![]() ; deducem acum :
; deducem acum : ![]() , de unde avem ca patrulaterul
, de unde avem ca patrulaterul ![]() este inscriptibil ,
deci I este de fapt punctul D . În continuare , deoarece triunghiurile
este inscriptibil ,
deci I este de fapt punctul D . În continuare , deoarece triunghiurile ![]() si
si ![]() sunt isoscele (
sunt isoscele ( ![]() si
si ![]() - mediane
corespunzatoare ipotenuzelor . ) , iar
- mediane
corespunzatoare ipotenuzelor . ) , iar ![]() , deducem ca
, deducem ca ![]() este tangenta
comuna celor doua cercuri ( tangenta in
este tangenta
comuna celor doua cercuri ( tangenta in ![]() ) . Cum HD ( sau HI )
este axa radicala a cercurilor respective , obtinem ca HI
intersecteaza
) . Cum HD ( sau HI )
este axa radicala a cercurilor respective , obtinem ca HI
intersecteaza ![]() in mijlocul acestuia . ■
in mijlocul acestuia . ■
Problema 9. În triunghiul ABC se
noteaza ![]() . Cercurile cu centrele in A , B si C de raze
respectiv
. Cercurile cu centrele in A , B si C de raze
respectiv ![]() intersecteaza
laturile triunghiului in sase puncte ( discurile respective sunt
doua cate doua disjuncte).Demonstrati ca cele
sase puncte sunt conciclice daca si numai daca exista
egalitatile :
intersecteaza
laturile triunghiului in sase puncte ( discurile respective sunt
doua cate doua disjuncte).Demonstrati ca cele
sase puncte sunt conciclice daca si numai daca exista
egalitatile :
![]() si
si ![]() .
.
(I.V.Maftei,A.Ghioca,ONM 1983)
Solutie : Notam ![]()
![]() Presupunem ca M,N,P,Q,R,S sunt conciclice.Folosind
puterea punctului A fata de cercul ce contine cele sase
puncte avem :
Presupunem ca M,N,P,Q,R,S sunt conciclice.Folosind
puterea punctului A fata de cercul ce contine cele sase
puncte avem :
![]() , adica
, adica ![]() ;analog,cu puterea punctului C fata de acelasi
cerc,avem
;analog,cu puterea punctului C fata de acelasi
cerc,avem ![]() . Reciproc,presupunand adevarate
egalitatile
. Reciproc,presupunand adevarate
egalitatile ![]() si
si ![]() , vom arata
ca hexagonul MNPQRS este inscriptibil; vom demonstra asadar ca
mediatoarele laturilor sale sunt concurente.În primul rand,sa
observam ca mediatoarele laturilor
, vom arata
ca hexagonul MNPQRS este inscriptibil; vom demonstra asadar ca
mediatoarele laturilor sale sunt concurente.În primul rand,sa
observam ca mediatoarele laturilor![]() sunt concurente , fiind bisectoarele unghiurilor triunghiului
ABC;notam punctul de concurenta cu O si aratam ca
O este situat si pe celelalte mediatoare. Notam cu K , L , I
proiectiile lui O pe dreptele BC , CA , AB. Cum O este pe mediatoarea lui
sunt concurente , fiind bisectoarele unghiurilor triunghiului
ABC;notam punctul de concurenta cu O si aratam ca
O este situat si pe celelalte mediatoare. Notam cu K , L , I
proiectiile lui O pe dreptele BC , CA , AB. Cum O este pe mediatoarea lui ![]() ,avem :
,avem : ![]() si deoarece aceasta mediatoare este si
bisectoarea unghiului
si deoarece aceasta mediatoare este si
bisectoarea unghiului ![]() ,deducem :
,deducem : ![]() Obtinem astfel :
Obtinem astfel : ![]() si , analog ,
si , analog , ![]() .Ajungem acum la :
.Ajungem acum la : ![]() . Folosind ipoteza
. Folosind ipoteza ![]() ,deducem
,deducem ![]() si apoi
si apoi ![]() Analog,din ipoteza
Analog,din ipoteza ![]() , ajungem
, ajungem ![]() Din
Din![]() , adica
, adica ![]() sunt mediatoarele
laturilor
sunt mediatoarele
laturilor ![]() ale hexagonului .
■
ale hexagonului .
■
Problema 10.Fie ![]() tangenta comuna a
doua cercuri de centre
tangenta comuna a
doua cercuri de centre ![]() si
si ![]() , secante in A
si B . Dreapta AB intersecteaza a doua oara cercul circumscris
triunghiului
, secante in A
si B . Dreapta AB intersecteaza a doua oara cercul circumscris
triunghiului ![]() in M . Sa
se stabileasca natura patrulaterului
in M . Sa
se stabileasca natura patrulaterului ![]()
(C.Cosnita , Rev.Pitagora,1939)
Solutie : Folosim observatia 2 , Problema 7 si
astfel punctul N de intersectie dintre axa radicala a cercurilor
si tangenta comuna are proprietatea ca ![]() .Observam ca
.Observam ca ![]() si
si ![]() , asadar
, asadar ![]() . Cum insa
. Cum insa ![]() ,deducem si
,deducem si ![]() , asadar
, asadar ![]() este paralelogram.
■
este paralelogram.
■
Problema 11. În triunghiul ABC ,
bisectoarea unghiului ![]() intersecteaza
latura (BC) in D. Se considera cercul ω tangent
intersecteaza
latura (BC) in D. Se considera cercul ω tangent
(Concurs Iran , 1998)
Solutie : Notam cu ![]() .Evident,
.Evident,![]() .
.
Deoarece APDM este patrulater inscriptibil,avem imediat :
![]() . Cum insa DC este tangenta la ω
in D , deducem :
. Cum insa DC este tangenta la ω
in D , deducem : ![]() Acum , din
Acum , din
![]() ajungem la :
ajungem la : ![]() . Asadar :
. Asadar :
![]() Obtinem acum :
Obtinem acum : ![]() .
.
Asadar ![]() si astfel BC este
tangenta la cercul circumscris triunghiului APB.Deducem acum ca AP
este axa radicala a celor doua cercuri ( ω si cercul
circumscris triunghiului APB ) , care intersecteaza tangenta comuna
in punctul T. Deoarece T este pa axa radicala,el are puteri egale
fata de cele doua cercuri,adica :
si astfel BC este
tangenta la cercul circumscris triunghiului APB.Deducem acum ca AP
este axa radicala a celor doua cercuri ( ω si cercul
circumscris triunghiului APB ) , care intersecteaza tangenta comuna
in punctul T. Deoarece T este pa axa radicala,el are puteri egale
fata de cele doua cercuri,adica : ![]() , deci P se afla pe mediana din A a triunghiului APB.
■
, deci P se afla pe mediana din A a triunghiului APB.
■
Problema 12. Se considera un triunghi ABC
si ![]() astfel
incat
astfel
incat ![]() iar P un punct in interiorul triunghiului ADE.Se
noteaza
iar P un punct in interiorul triunghiului ADE.Se
noteaza ![]() Daca O este centrul cercului circumscris triunghiului
PDG , iar Q centrul cercului circumscris triunghiului PEF , sa se arate
ca
Daca O este centrul cercului circumscris triunghiului
PDG , iar Q centrul cercului circumscris triunghiului PEF , sa se arate
ca ![]()
Solutie : Deoarece cele doua cercuri se
intersecteaza in P , este suficient sa aratam ca
AP este axa lor radicala.Notam ![]() Din
Din ![]() si astfel
si astfel ![]() , adica H se
afla pe axa radicala.Cum
, adica H se
afla pe axa radicala.Cum ![]() ,concluzia este imediata. ■
,concluzia este imediata. ■
În incheiere,va propunem sa va incercati puterile cu urmatoarea problema :
Fie ABC un triunghi si in
interiorul sau doua cercuri ![]() si
si ![]() care se
intersecteaza in punctele M si N si astfel
incat
care se
intersecteaza in punctele M si N si astfel
incat ![]() este tangent dreptelor
AB si BC , iar
este tangent dreptelor
AB si BC , iar ![]() este tangent dreptelor
AC si BC. Sa se arate ca daca M si N sunt situate pe
mediana din A a triunghiului ABC , atunci ABC este triunghi isoscel. Reciproca
este adevarata ?
este tangent dreptelor
AC si BC. Sa se arate ca daca M si N sunt situate pe
mediana din A a triunghiului ABC , atunci ABC este triunghi isoscel. Reciproca
este adevarata ?
(Lucian Dragomir , G.M.)
Bibliografie :
D.M.Batinetu-Giurgiu si colectiv - Probleme date la olimpiadele de matematica pentru licee(1950-1990),Ed. Stiintifica, Bucuresti,1992
M.St.Botez - Probleme de geometrie , Ed. Tehnica , Bucuresti , 1976
A.Cota si colectiv - Matematica pentru clasa a IX a , manual , E.D.P. 1988
A.Leonte,R.Trandafir - Principii si structuri fundamentale in matematica de liceu , Ed. Albatros , Bucuresti , 1986
L.Nicolescu , V. Boskoff - Probleme practice de geometrie , Ed. Tehnica , Bucuresti , 1990
Gazeta Matematica , colectia 1983- 2006
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |