
METODA INDUCTIEI MATEMATICE COMPLETE, ANALIZA COMBINATORIE, BINOMUL LUI NEWTON, SUME
Inductie matematica
1. Inductie
a) 13 + 33 + 53 + + (2n - 1)3 = n2(2n2 - 1)
b) 12
- 22 + 32 - 42 + + (-1)n-1 n2
= ![]()
c) ![]()
d) ![]()
e) ![]()
.2. Inductie
a) x I Z a.i. 3x + 1 < 2log2(x
+ 4) ; b) ![]()
c) n ![]() ;
;
d) a, b I R, a + b > 0, a b, n ![]()
e) 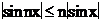 f)
f) ![]()
g) ![]()
h) ![]()
i) ![]()
j) n , ![]()
3 Inductie
a) ![]() a1
a1 ![]() an & b1
an & b1
![]() bnI R
bnI R
b) n 2, a1 an > si a1 a2 an = 1, atunci a1 + a2 + + an n
c) 2n
n2 + 1, n 5; d) n 3, nn+1 > (n + 1)n
, n ![]()
e) 32n+1
+ 2n+2 ![]() n I N* ; f) 9n+1 + 8n - 9
n I N* ; f) 9n+1 + 8n - 9 ![]() n I N*
n I N*
g) n3
+ 11n ![]() n I N*
n I N*
4 Sa se calculeze: 5. Sa se rezolve ecuatiile:
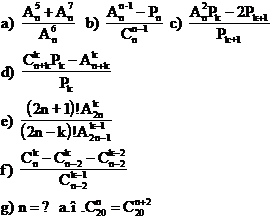
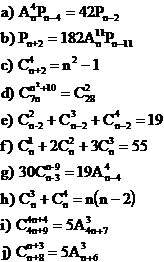
6 Sa se rezolve ecuatiile:
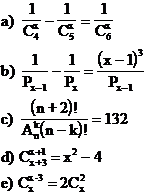
7 a) Fie f: D R, f(x) = ![]()
Daca
![]() , atunci A = ?
, atunci A = ?
b)
Sa se determine x pentru care nr. ![]() este definit; x I Z.
este definit; x I Z.
c) Sa se rezolve ecuatiile:
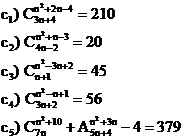
8. Rezolvati:
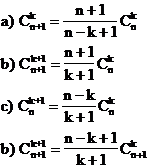
![]() este patrat
perfect
este patrat
perfect
f)
Sa se demonstreze ca n 2 avem ![]()
9. a) Sa se rezolve ecuatia: ![]()
b) 1. Sa se
rezolve ecuatia: ![]()
2. Sa se
arate ca ![]() nu se divide cu 7.
nu se divide cu 7.
3. Sa se arate ca a, b I N, a!b! divide pe (a + b)!
c) 1. Sa se rezolve in c ecuatia:
![]()
2. Sa se arate ca:
a) ![]() ; b)
; b) ![]()
c) ![]() ; d)
; d) ![]()
e) ![]() ; f)
; f) ![]()
3. Sa se arate ca pentru n par atunci:
![]()
4. Sa se calculeze, pentru n
![]()
5. Sa se
calculeze: ![]() ; 6. Sa se arate ca:
; 6. Sa se arate ca: ![]()
d) 1. Rezolvati ecuatia: ![]() , n, k I N
, n, k I N
2. Sa se arate ca numerele ![]() si
si ![]() sunt numere naturale,
sunt numere naturale,
n,p I N
10 Sa se determine:
1. a) T8
al dezvoltarii (2x + a)10 ; b) T mijloc al dezvoltarii ![]()
c) Tk
al dezvoltarii ![]() care il contine pe x0 (in care nu apare x)
care il contine pe x0 (in care nu apare x)
d)
rangul termenului din dezvoltarea 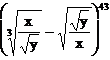 in care x si y au puteri egale
in care x si y au puteri egale
2. Se
considera dezvoltarea ![]() . Sa se determine:
. Sa se determine:
a) termenul care contine pe x5; b) termenul care contine pe a20
c) termenul in care x si a au puteri egal ; d) termenul care nu contine pe x
e) termenul care contine pe a ; f) termenul din mijloc al dezvoltarii
3. In dezvoltarea ![]() suma coeficientilor binomiali de rang par este 4096.
Sa se calculeze:
suma coeficientilor binomiali de rang par este 4096.
Sa se calculeze:
a) termenul care nu contine pe x
b) termenul care nu-l contine pe a
c) termenul in care x si a au puteri egale
d) termenul care contine pe a
e) termenul care contine pe x
4. a) Sa
se determine n, daca coeficientul binomial al termenului de rang 3 al
dezvoltarii ![]() este 190.
este 190.
b) In
dezvoltarea 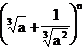 suma coeficientilor binomiali de rang impar este
egala cu 256. Sa se gaseasca termenul care contine pe
1/a.
suma coeficientilor binomiali de rang impar este
egala cu 256. Sa se gaseasca termenul care contine pe
1/a.
c)
Sa se determine m.m.p. a.i. in dezvoltarea ![]() termenii
de rang 12 si 24 sa contina pe x, respectiv pe x5
si, aceasta dezvoltare sa aiba termen liber.
termenii
de rang 12 si 24 sa contina pe x, respectiv pe x5
si, aceasta dezvoltare sa aiba termen liber.
d) Fie
dezvoltarea 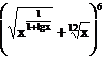 . Sa se afle x stiind ca al patrulea termen al
dezvoltarii este egal cu 200.
. Sa se afle x stiind ca al patrulea termen al
dezvoltarii este egal cu 200.
e)
Sa se determine n si x daca, in dezvoltarea 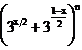 suma coeficientilor binomiali ai primilor 3 termeni este
egala cu 22, iar suma dintre termenul al treilea si termenul al
cincilea este 420.
suma coeficientilor binomiali ai primilor 3 termeni este
egala cu 22, iar suma dintre termenul al treilea si termenul al
cincilea este 420.
5. Sa se gaseasca rangul termenului cel mai mare:
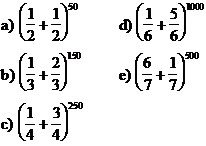
6. Fie dezvoltarea (2 + m)m, m I N, m 2. Sa se determine m astfel incat termenul:
a) T3 sa fie cel mai mare din dezvoltare
b) T10 sa fie cel mai mare din dezvoltare
c) T50 sa fie cel mai mare din dezvoltare
7. Sa se gaseasca suma coeficientilor din dezvoltarea:
|
a |
(9x2 - 6y2)50 |
d |
(5x2 - 4y2)100 |
|
|
b |
(18x - 8y)50 |
e |
(7x2 - 6y2)n |
|
|
c |
(7x3 - 6y)1000 |
f |
(9x - 6y)n |
11 1. Sa se determine termenii rationali ai dezvoltarilor urmatoare:
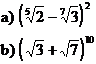
2. Sa se determine termenii rationali ai dezvoltarilor:
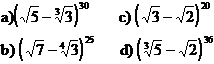
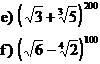
3. Sa se determine x, y, n I N daca in dezvoltarea:
a) 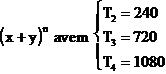 b)
b) 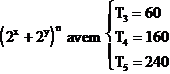
c) ![]() d)
d) 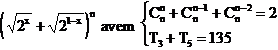
e) ![]()
4. Sa se gaseasca coeficientii lui:
a) x3 din dezvoltarea (1 + x + x2)10
b) x6 din dezvoltarea (2 - 3x + x2)6
c) x10 din dezvoltarea (1 - x + x2 - x3)10
d) x8 din dezvoltarea (1 - 2x + 3x2 - 4x3)4
5. Sa se determine coeficientii termenului care contine pe:
a) x3 in produsul (1 + x)4(1 - x)7
b) x4 in produsul (1 + x)5(1 - x)3
c) x5 in produsul (2 - 3x)4(5 - 7 x2)10
6. Sa se determine termenii care nu contine pe a, din dezvoltarea:
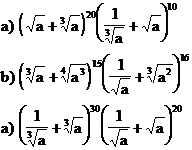
7. Sa se determine x daca in dezvoltarea:
a) ![]() avem T4 = 200
avem T4 = 200
b) ![]() avem T3 =
106
avem T3 =
106
c) 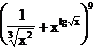 avem T3 =
36000
avem T3 =
36000
8. a) Sa se determine termenul care nu-l contine pe x din dezvoltarea:
![]()
b) Se
considera ![]() , p I N, x > 0. Sa se determine
termenul care nu contine pe x.
, p I N, x > 0. Sa se determine
termenul care nu contine pe x.
c)
Sa se determine termenii irationali ai dezvoltarii ![]()
d)
Sa se determine numarul termenilor rationali ai dezvoltarii
![]()
e) In
dezvoltarea ![]() suma
coeficientilor binomiali de rang par este egala cu 128. Sa se
determine termenul care contine pe a3.
suma
coeficientilor binomiali de rang par este egala cu 128. Sa se
determine termenul care contine pe a3.
f)
Sa se afle T10 al dezvoltarii ![]()
9. a) Sa se determine n, daca in dezvoltarea (1 + x)n coeficientii lui x5 si x12 sunt egali.
b)
Sa se arate ca n 2 si ![]() avem (1 + x)n + (1 - x)n 2n
avem (1 + x)n + (1 - x)n 2n
c)
Sa se arate ca ![]()
Progresii aritmetice si geometrice
1. Sa se scrie primii 5
termeni ai ![]() (an) daca:
(an) daca:
a) a1 = 2, r = - 3; b) a10 = 131, r = 12; c) a5 = 27, a27 = 6; d) a3 = 11, a5 = 19
Sa se scrie formula pentru (an)n
2. a) Sa se determine a1, a3, a5,
a6 ![]() pentru urmatoarea
ordine a1, - 7, a3, -1, a5, a6, 8,
pentru urmatoarea
ordine a1, - 7, a3, -1, a5, a6, 8,
b) Sa se gaseasca a1 si r daca:
![]()
![]()
c) Se da
(a + b)n, ![]() si
si ![]()
Sa
se determine x stiind ca termenul dezvoltarii care contine
pe b5 este 21, iar coeficientii binominali ai celui de-al
doilea, al treilea si al patrulea termen al dezvoltarii binomului
sunt in ![]()
3. Cunoscand suma Sn, sa se determine:
a)
primii S termeni ai ![]() , daca
, daca ![]()
b)
primul termen si ratia ![]() , daca Sn = 2n2 + 3n
, daca Sn = 2n2 + 3n
c) ratia si an, daca Sn = 3n2 + 4n
4. a) Fie (an)n , Sn = a1 + a2
+ + an, n > 0. Sa se arate ca daca
Sn = a n2
+ b n unde a, b sunt numere reale
date atunci sirul an formeaza ![]()
b) Fie Sn
= a1 + a2 + + an, n 1. Sa se arate ca Sn
= a n2 + b n + c, unde a, b, c I R atunci (an), ![]() c =
c =
c) Fie (an),
![]() . Daca am = n si an = m, m n sa se calculeze ap,
p I N*
. Daca am = n si an = m, m n sa se calculeze ap,
p I N*
d) Daca ![]() an
an ![]() , sa se calculeze ap, Sp, p I N
, sa se calculeze ap, Sp, p I N
5. a) Fie (an) n ![]() , Sk suma primilor k termeni ai sai. Daca
Sm = m si Sn = n, m n atunci: Sp = p, p I N.
, Sk suma primilor k termeni ai sai. Daca
Sm = m si Sn = n, m n atunci: Sp = p, p I N.
b) Intr-o ![]() (an)n , a1 = 1 si
(an)n , a1 = 1 si ![]() . Sa se determine progresia.
. Sa se determine progresia.
c) Fie (an)n ![]() , Sk suma primilor k termeni ai sai. Sa
se arate ca daca
, Sk suma primilor k termeni ai sai. Sa
se arate ca daca ![]() atunci
atunci ![]() , m n.
, m n.
d) Sa se gaseasca
suma primilor 20 termeni ai unei ![]() daca:
daca:
a6 + a9 + a12 + a15 = 20.
e) Intr-o progresie aritmetica avem S10 = 100, S30 = 900. Sa se determine S50.
f) Sa se rezolve ecuatiile:
1 + 7 + 13 + + x = 280
(x + 1) + (x + 4) +(x + 7) + + (x + 28) = 155
6. A. Sa se demonstreze ca numerele sunt in ![]()
a) ![]()
b) ![]()
B. Sa se demonstreze
ca daca a, b, c ![]() atunci si
numerele urmatoare sunt in
atunci si
numerele urmatoare sunt in ![]()
a) a2 - bc, b2 - ca, c2 - ab
b) b2 + c2 + bc, c2 + ac + a2, a2 + ab + b2
Sa se arate ca daca a + b + c atunci este adevarata si reciproca.
c. Sa
se demonstreze ca daca a2, b2, c2 ![]() atunci:
atunci:
a) ![]()
b) ![]() sunt in
sunt in ![]()
C.a) Fie x1, x2, , xn un sir de numere reale nenule.
Sa se arate ca acest sir este o progresie aritmetica daca si numai daca pentru n 2 avem relatia:
![]()
b) Sa
se arate ca daca lungimile laturilor unui triunghi dreptunghic sunt
in ![]() atunci ele sunt proportionale
cu numerele 3, 4, 5.
atunci ele sunt proportionale
cu numerele 3, 4, 5.
c) Fie
(an) ![]() si (bn) astfel incat a1 + a2 +
+ a10 = 155, b1 + b2 = 9. Sa se
determine progresiile, daca a1 este ratia
si (bn) astfel incat a1 + a2 +
+ a10 = 155, b1 + b2 = 9. Sa se
determine progresiile, daca a1 este ratia ![]() iar b1 este
ratia
iar b1 este
ratia ![]()
d) Fie
(an) ![]() si (bn)
si (bn)
![]() astfel incat a1
= b1, a2 = b2, a3 = b3 -
8. Sa se determine progresiile.
astfel incat a1
= b1, a2 = b2, a3 = b3 -
8. Sa se determine progresiile.
e) Sa
se arate ca daca n si k sunt numere naturale cu n k + 3 atunci ![]()
![]()
![]()
![]() nu pot fi termenii
consecutivi ai unei progresii aritmetice.
nu pot fi termenii
consecutivi ai unei progresii aritmetice.
7. A. Sa se gaseasca primul termen si ratia
unei ![]() (an)n , daca:
(an)n , daca:
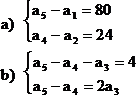
![]()
B. Sa se
scrie primii 5 termeni ai ![]() (bn) daca:
(bn) daca:
a) b1 = 3, q = - 2
b) b8 = 384, q = 2
c) b6 = 25, b8 = 9
d) b3 = 20, b9 = 1280
C. Sa se gaseasca termenii b2, b3,
b5, b6 ai ![]() urmatoare:
urmatoare: ![]() , b2, b3, 12
, b2, b3, 12![]() , b5, b6, 216
, b5, b6, 216![]()
D. Sa se
determine (bn)n ![]() date prin:
date prin:
a) b1 = 2, bn+1 = 3bn
b) b1 = 4, bn+1 = - 3bn
c) b1 = 9, bn+1 = 2bn
d) b1
= 10, bn+1 = ![]() bn
bn
E. Fie a1,
a2, a3, a4, a5 ![]() astfel incat suma
logaritmilor in baza 3 a acestor numere sa fie egala cu 2. Sa se
gaseasca aceste numere stiind ca:
astfel incat suma
logaritmilor in baza 3 a acestor numere sa fie egala cu 2. Sa se
gaseasca aceste numere stiind ca:
![]()
8. a) Suma a1 + a2 + a3 + a4
+ a5 = 62, a1, a2, a3, a4,
a5 ![]()
Daca
termenii al 5-lea, al 8-lea si al 11-lea ai acestei progresii sunt primul,
al 2-lea si al 10-lea termen pentru o progresie ˜, sa se gaseasca
primul termen al ![]()
b) Fie
a, b, c ai a + b + c = 124 astfel incat sa fie termenii consecutivi a.i. ![]() . Daca a, b, c sunt al 3-lea, al 13-lea si al
15-lea termen al
. Daca a, b, c sunt al 3-lea, al 13-lea si al
15-lea termen al ![]() , sa se determine a, b, c.
, sa se determine a, b, c.
c) Fie a1
+ a2 + + a13 = 130, a1, a2,
, a13 ![]()
Presupunem
ca termenii: al 4-lea, al 10-lea, al saptelea sunt 3 termeni
consecutivi ai unei ![]() , sa se determine primul termen al
, sa se determine primul termen al ![]()
d) Fie
(an) ![]() cu termeni pozitivi
a.i.
cu termeni pozitivi
a.i. ![]() . Sa se demonstreze ca a4, a6,
a9
. Sa se demonstreze ca a4, a6,
a9 ![]() . Sa se determine ratia.
. Sa se determine ratia.
e) Fie a1,
a2, ., a2n+2 ![]() descrescatoare.
Sa se demonstreze ca:
descrescatoare.
Sa se demonstreze ca:
![]() <
< 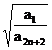
f) Fie yn
![]() a.i. suma Sn
= 2(5n - 1). Sa se determine Sn, y1, y2.
a.i. suma Sn
= 2(5n - 1). Sa se determine Sn, y1, y2.
g) Nr.
a, b, c ![]() cu ratia r iar
nr. a, b + 1, c + 6
cu ratia r iar
nr. a, b + 1, c + 6 ![]() cu ratia r + 2.
Sa se determine
cu ratia r + 2.
Sa se determine ![]()
![]()
9.A) Daca a1, a2, ., an ![]() de ratie r,
sa se calculeze:
de ratie r,
sa se calculeze:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
B) Sa se determine ![]() a1, a2,
., an a. i.
a1, a2,
., an a. i.
a) ![]()
b) ![]()
C) Daca a1,
a2, ., an ![]() de ratie r, are
loc egalitatea:
de ratie r, are
loc egalitatea:
![]()
D) Daca a0,
a1, a2, ., ak ![]() sa se calculeze:
sa se calculeze:
a) S = a2 + a4 + a6 + . + a2n
b) ![]()
c) 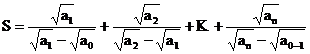
1. a) Fie a1,
a2, ., an ![]() si S1
= a1+ a2+ .+ an
si S1
= a1+ a2+ .+ an
![]() . Sa se determine, in functie de S1
si S2, produsul
. Sa se determine, in functie de S1
si S2, produsul
P = a1 a2 an.
b) Daca
a1, a2, ., an ![]() , sa se arate ca:
, sa se arate ca:
![]()
c) Fie
nr. pozitive a1, a2, ., an ![]() , p I N*.
, p I N*.
Sa se arate ca raportul sumelor:
![]() si
si
![]()
nu depinde de n.
d) Sa se rezolve ecuatia:
1 + x + x2 + . + x99 = 0
e)
Sa se determine x a.i. nr. a + x, b + x, c + x sa fie in ![]()
2. Se dau nr. a si b. Sa se determine x, y, z a.i. sa fie satisfacute simultan conditiile:
a) x, y,
z ![]() ; b) x, y + a, z
; b) x, y + a, z ![]() c) x, y + a, z + b
c) x, y + a, z + b
![]()
Caz particular: a = 4, b = 82.
3. a) Aflati x,
y a. i. ![]()
![]()
b) Aratati ca ![]()
![]()
c) Daca a, b, c ![]() atunci abcd + (b - a)4
este patrat perfect.
atunci abcd + (b - a)4
este patrat perfect.
d) Fie ![]() a1, a2,
., a5. Aflati a1 daca:
a1, a2,
., a5. Aflati a1 daca:
![]() si
si ![]()
e) Fie x, y, z ![]() . Stiind ca suma lor este 30 si ca
succesiunea x - 5, y - 4, z
. Stiind ca suma lor este 30 si ca
succesiunea x - 5, y - 4, z ![]() , sa se determine x, y, z.
, sa se determine x, y, z.
f) Fie a, b, c nr. ![]() . Stiind ca a - 2, b - 6, c - 7, d - 2
. Stiind ca a - 2, b - 6, c - 7, d - 2 ![]() , determinati a, b, c, d.
, determinati a, b, c, d.
g) Determinati egalitatea:
![]()
Calculul sumelor
I. Folosind sumele elementare (S1, S2, S3, S4)
Sa se calculeze S si sa se verifice prin inductie:
a) ![]()
b) 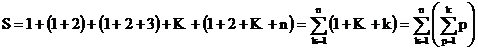
c) ![]() d)
d) ![]()
e) ![]()
f) ![]()
II. Folosind metoda desfacerii in fractii simple
1. Sa se calculeze S si sa se verifice prin inductie
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
2. a)
Sa se calculeze: ![]()
b) Sa se calculeze: ![]()
III. Folosind artificii de calcul
1. Sa se calculeze:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ;
;
d) ![]() ; e)
; e) ![]() ; f)
; f) ![]()
g) ![]() ; h)
; h) ![]() ; i)
; i) ![]()
2. Sa se calculeze sumele urmatoare:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
d) ![]() ; e)
; e) ![]() ; f)
; f) ![]()
IV. Folosind derivate pentru sume de combinari
1. Sa se calculeze sumele urmatoare:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
2. Sa se calculeze:
a) ![]() ; b)
; b) ![]()
c) ![]() ; d)
; d) ![]()
e) ![]()
f) ![]()
V. Folosind integrale pentru sume de combinari
Sa se
calculeze: a) ![]()
b) ![]() ; c)
; c) ![]()
d) ![]()
e) ![]()
VI. Folosind nr. complexe sub forma trigonometrica si identitatea a doua nr. complexe
1. Sa se calculeze:
a) ![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |