
Automatul de ordinul zero. Circuite logice combinationale
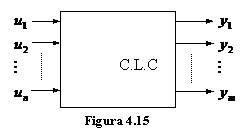
Pentru acest circuit se poate scrie setul de functii:
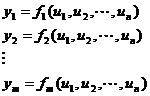
unde ![]() sunt functii logice.
sunt functii logice.
Legat de realizabilitatea fizica a circuitelor logice combinationale se pot formula doua tipuri de probleme: de sinteza si de analiza. In continuare se vor dezvolta aceste probleme.
1. Sinteza si analiza circuitelor logice combinationale
Problemele de sinteza ale circuitelor logice combinationale se definesc in modul urmator: cunoscand semnalele de iesire corespunzatoare diferitelor combinatii ale semnalelor de intrare se cere sa se stabileasca structura circuitului logic combinational.
In general, sinteza unui circuit logic combinational presupune parcurgerea urmatoarelor etape:
1) Pe baza enuntului temei de proiectare se procedeaza la completarea tabelului de adevar;
2) Se realizeaza minimizarea functiilor logice prin una din metodele cunoscute;
3) Se implementeaza functiile logice obtinute cu circuite logice;
4) Se analizeaza circuitul obtinut pentru a vedea daca corespunde conditiilor impuse initial.
In cadrul problemelor de analiza se cunoaste structura logica a circuitului combinational si se cere sa se stabileasca valorile posibile ale semnalelor de iesire pentru toate combinatiile posibile de valori ale semnalelor de intrare. Problemele de analiza se solutioneaza cautand expresiile functiilor logice corespunzatoare semnalelor de iesire pentru ca ulterior sa se poata determina valorile acestor functii pentru toate combinatiile posibile de valori ale semnalelor de intrare. Pentru a putea determina valorile acestor functii este necesar sa se gaseasca termenii canonici ai functiei. Etapele ce trebuiesc parcurse in vederea analizei unui circuit combinational sunt:
1) Pe baza structurii logice a circuitului logic combinational se determina, din aproape in aproape functiile logice ale semnalelor de iesire in forma normala;
2) Se dezvolta aceste functii logice in forma canonica;
3) Folosind tabelul de adevar se stabilesc valorile functiilor corespunzatoare semnalelor de iesire pentru toate combinatiile posibile de valori ale semnalelor de intrare;
4) O etapa neobligatorie, dar uneori interesanta, consta in stabilirea de expresii minimale ale functiilor logice in forma canonica. Aceasta etapa vizeaza realizarea unui circuit echivalent cu circuitul analizat, dar mai economic. Nu trebuie omis insa faptul ca in procesul de sinteza au putut interveni si alte criterii decat cel de economicitate (de ex. functionare fara hazard).
2. Circuite logice combinationale sintetizate cu porti logice
Sinteza circuitelor logice combinationale cu porti logice (adica cu acele circuite logice care materializeaza fizic functiile logice elementare) presupune ca etapa obligatorie minimizarea functiilor logice in forma normala disjunctiva sau conjunctiva. Operatia de implementare a functiilor logice in scheme cu porti logice constituie o problema de optimizare a carei rezolvare depinde de experienta proiectantului in conditiile existentei unor restrictii privind: numarul de porti logice intr-o capsula de circuit integrat; numarul de intrari ale fiecarei porti logice; tipul de poarta logica care asigura utilizarea numarului minim de capsule integrate; etc.
Observatie: la sinteza circuitelor logice combinationale cu mai multe variabile de iesire se poate obtine o reducere a numarului de porti logice folosite daca se identifica termeni comuni in expresiile functiilor de iesire.
2.1. Sinteza cu porti logice NU, SI, SAU
La baza sintezei circuitelor combinationale cu porti logice NU, SI, SAU sta forma normala minima disjunctiva a functiei logice, atunci cand variabilele de intrare ale circuitului combinational se aplica la intrarile unor porti logice SI, iar iesrile se culeg de la iesirile unor porti logice de tip SAU, respectiv forma normala minima conjunctiva a functiei, atunci cand variabilele de intrare ale circuitului combinational se aplica la intrarile unor porti logice SAU, iar iesirile se culeg de la iesirile unor porti logice SI. Se mai spune ca circuitele combinationale ce implementeaza functii logice in forma normala disjunctiva au pe nivelul de intrare porti logice de tip SI respectiv pe nivelul de iesire porti logice de tip SAU si respectiv invers pentru circuitele combinationale ce implementeaza functii logice in forma normala conjunctiva. Formele normale ale functiilor logice descriu structural schema logica a circuitului ce trebuie realizat.
In practica, sinteza cu porti logice NU, SI, SAU, dispuse pe doua nivele, ridica probleme numai atunci cand portile logice folosite au un numar de intrari mai mic decat cel necesar, unele sunt incarcate peste limita de sarcina admisa, respectiv unele iesiri nu pot realiza comanda tuturor circuitelor care s-ar impune conform expresiei logice.
In practica sinteza cu porti logice SI, SAU, NU este folosita arareori intrucat in familia de circuite integrate TTL, care este familia cea mai utilizata, exista o gama restransa de circuite integrate care implementeaza functiile logice SI, respectiv SAU.
Din acelasi motiv se practica sinteza utilizand portile logice SI-NU, respectiv SAU-NU.
2.2. Sinteza cu porti logice SI-NU, respectiv SAU-NU
Functiile logice NU, SI, SAU formeaza un sistem logic complet intrucat orice functie logica poate fi implementata cu circuite care materializeaza functiile logice NU, SI, SAU.
Exista si alte sisteme logice complete, dintre acestea mai frecvent utilizate fiind sistemele bazate pe functiile logice SI-NU respectiv SAU-NU. Pentru a demonstra ca si aceste functii formeaza un sistem logic complet este suficient sa demonstram ca ele pot implementa functiile logice NU, SI, SAU.
Observatii: Daca aplicam teoremele lui De Morgan pentru cele doua functii logice rezulta:
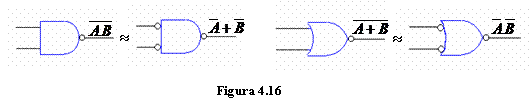
1) Un circuit SI-NU poate fi interpretat ca fiind compus dintr-un circuit SI urmat de un inversor sau ca un circuit SAU la care se aplica variabilele negate.
2) Un circuit SAU-NU poate fi interpretat ca fiind un circuit SAU urmat de un inversor sau ca un circuit SI la care se aplica variabilele negate.
Pornind de la aceste doua observatii, rezulta urmatoarele modalitati de implementare a functiilor logice NU, SI, SAU cu circuite ce materializeaza fizic functiile SI-NU, respectiv SAU-NU.
Functia logica NU poate fi implementata cu un circuit SI-NU daca la intrarile neutilizate se aplica semnalul logic "1", respectiv cu un circuit SAU-NU daca la intrarile neutilizate se aplica "0" logic. De asemenea functia NU poate fi implementata cu oricare din aceste circuite daca varibila ce trebuie negata se aplica la toate intrarile circuitului SI-NU, respectiv SAU-NU (fig. 4.17).
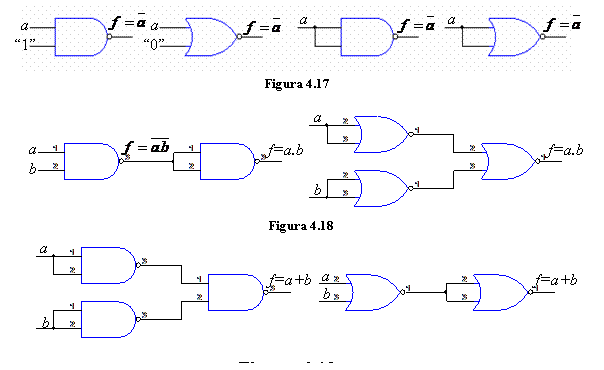
Functia logica SI poate fi implementata cu un circuit SI-NU urmat de un inversor sau cu un circuit SAU-NU la intrarile caruia se aplica varibilele negate (fig.4.18).
Functia logica SAU poate fi implementata cu un circuit SI-NU la intrarile caruia se aplica variabilele negate sau cu un circuit SAU-NU urmate de un inversor.
Rezulta deci ca orice functie logica poate fi implementata folosind numai circuite SI-NU, respectiv SAU-NU.
Pentru sinteza circuitelor logice combinationale cu circuite SI-NU se parcurg urmatoarele etape:
(a) - se obtine expresia minima a functiei in forma normala disjunctiva;
(b) - se realizeaza o schema logica cu circuite SI-NU plasate pe doua nivele;
(c) - variabilele care apar singure in suma se aplica la intrarea portii ce genereaza semnalul de iesire in forma complementata.
Exemplu:
![]() este
implementata de schema din fig. 4.20:
este
implementata de schema din fig. 4.20:
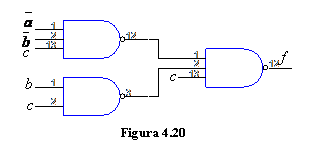
Pentru sinteza circuitelor logice combinationale cu circuite SAU-NU se parcurg urmatoarele etape:
(a) - se obtine expresia minima a functiei in forma normala conjunctiva;
(b) - se realizeaza o schema logica cu circuite SAU-NU plasate pe doua nivele;
(c) - variabilele care apar singure in produs se aplica la intrarea portii ce genereaza semnalul de iesire in forma complementata.
Exemplu:
![]() este
implementata de schema din fig.4.21:
este
implementata de schema din fig.4.21:
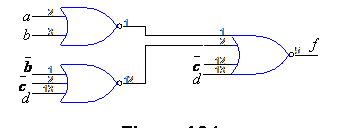
Observatie: Metodele prezentate in acest paragraf si in paragraful precedent sunt utilizate in general pentru implementarea functiilor logice simple. Pentru functii mai complicate se utilizeaza circuite integrate pe scara medie (ex. multiplexor, decodificator) sau larga (ex. memoria), circuite care realizeaza, in general, functii logice bine determinate. Pentru utilizarea lor la implementarea unor functii logice oarecare sunt necesare si porti logice.
3. Multiplexorul
Multiplexorul este un circuit logic combinational,
integrat pe scara medie, obtinut printr-o conexiune (extensie) de tip
serie a unor porti logice ce constituie elementul tipic de circuit logic
combinational. Din punct de vedere functional multiplexorul este un
selector ce conecteaza la iesire intrarea adresata. Circuitul
are in general ![]() intrari de date si "n" intrari
de adresa. Valoarea iesirii este determinata de valoarea
intrarii selectate prin adresa.
intrari de date si "n" intrari
de adresa. Valoarea iesirii este determinata de valoarea
intrarii selectate prin adresa.
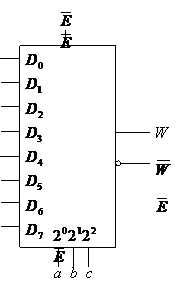
|
INTRARI |
IESIRI |
|||||||||||||
|
c |
b |
a |
|
|
|
|
|
|
|
|
|
|
W |
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
1 |
Figura 4.22
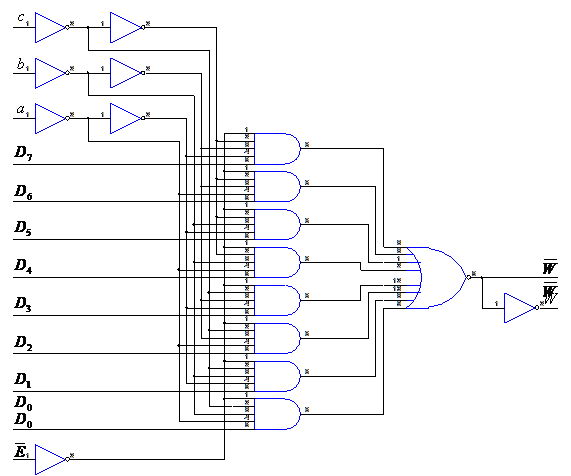
Sub
forma integrata se produc mai multe tipuri de multiplexoare dintre
care amintim multiplexorul cu 16 intrari de date si 4 intrari de
adresare, 8 intrari de date si 3 de adresare si 4 intrari
de date si 2 de adresare. In fig. 4.22 este data schema
desfasurata, schema bloc si tabelul de functionare ale
multiplexorului cu 8 intrari de date, 3 intrari de adresare, o
intrare de validare a functionarii (activa pe 0) si
doua iesiri complementare W si ![]() .
.
Functia logica pe care o implementeaza acest multiplexor este:
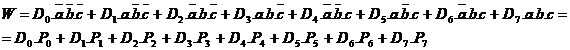 Dintre
aplicatiile posibile ale circuitelor multiplexoare amintim selectia
secventiala, conversia paralel-serie a datelor si transmisia
multiplexata a informatiilor de pe mai multe linii pe o singura
linie.
Dintre
aplicatiile posibile ale circuitelor multiplexoare amintim selectia
secventiala, conversia paralel-serie a datelor si transmisia
multiplexata a informatiilor de pe mai multe linii pe o singura
linie.
Pe langa aceste aplicatii multiplexoarele pot
fi utilizate si pentru implementarea functiilor logice. Astfel cu un
multiplexor cu ![]() intrari de date poate fi implementata
orice functie logica de "n" variabile aplicand la intrarile de
date valorile functiei, iar la intrarile de adresare cele "n"
variabile. De exemplu functia de trei variabile
intrari de date poate fi implementata
orice functie logica de "n" variabile aplicand la intrarile de
date valorile functiei, iar la intrarile de adresare cele "n"
variabile. De exemplu functia de trei variabile
![]()
este implementata de multiplexorul din fig. 4.23.
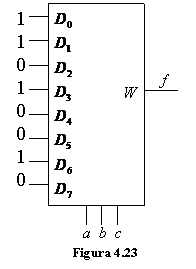
|
|
a |
b |
c |
d |
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
|
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
|
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
|
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
|
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
|
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
|
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
Figura 4.24
Un multiplexor cu ![]() intrari de date poate implementa si
functii de mai mult de "n" variabile daca se utilizeaza si
porti logice suplimentare. Pentru functii de "n+1" variabile se aleg
"n" variabile care se aplica la intrarile de adresare, iar a "n+1"
variabila se aplica in forma normala sau complementata
la unele intrari de date.
intrari de date poate implementa si
functii de mai mult de "n" variabile daca se utilizeaza si
porti logice suplimentare. Pentru functii de "n+1" variabile se aleg
"n" variabile care se aplica la intrarile de adresare, iar a "n+1"
variabila se aplica in forma normala sau complementata
la unele intrari de date.
Ex. functia ![]() definita prin tabelul si avand
reprezentarea in figura 4.24
definita prin tabelul si avand
reprezentarea in figura 4.24
Observatie: Pentru a usura determinarea functiilor de intrare din tabelul de definitie al functiei logice este recomandabil ca variabila reziduala sa fie cea mai putin semnificativa.
In general prin utilizarea circuitelor multiplexoare se
reduce numarul variabilelor de care depinde functia logica.
Astfel, daca functia de implementat depinde de "n" variabile, prin
utilizarea unui multiplexor cu ![]() intrari de date (m<n) functiile care
trebuiesc implementate cu porti logice depind de "n-m" variabile.
Implementarea functiei de "n" variabile se reduce in acest fel la
implementarea a
intrari de date (m<n) functiile care
trebuiesc implementate cu porti logice depind de "n-m" variabile.
Implementarea functiei de "n" variabile se reduce in acest fel la
implementarea a ![]() functii de "n-m" variabile.
functii de "n-m" variabile.
Pentru exemplificare se considera functia ![]() de cinci variabile la implementarea
careia se foloseste un multiplexor cu 8 intrari de date
(fig.4.25).
de cinci variabile la implementarea
careia se foloseste un multiplexor cu 8 intrari de date
(fig.4.25).
|
a |
b |
c |
d |
e |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
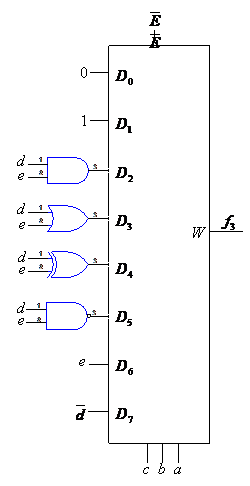
|
0 |
1 |
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
0 |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
1 |
0 |
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
0 |
Figura 4.25
4. Decodificatorul si demultiplexorul
Decodificatorul
este un circuit logic combinational, integrat pe
scara medie, obtinut printr-o extensie de tip paralel a unor
porti logice si are "n" intrari de adresare si ![]() iesiri. Din punct de vedere functional
decodificatorul activeaza una din cele
iesiri. Din punct de vedere functional
decodificatorul activeaza una din cele ![]() iesiri ale sale, functie de codul
aplicat la cele "n" intrari.
iesiri ale sale, functie de codul
aplicat la cele "n" intrari.

|
INTRARI |
IESIRI |
|||||||||
|
a |
b |
c |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
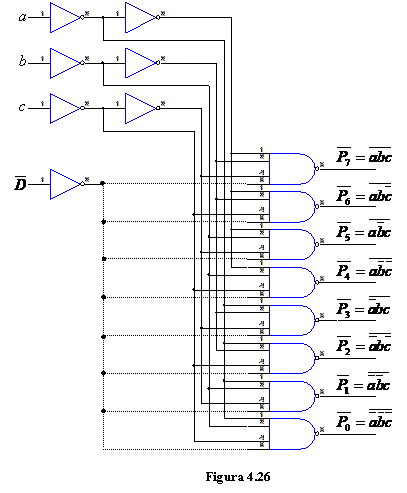
Circuitul decodificator din fig.4.26 se transforma in circuit demultiplexor daca schema se completeaza cu traseele cu linie intrerupta.
Din punct
de vedere functional demultiplexorul asigura transmiterea semnalului
aplicat la intrarea sa prin una din cele ![]() iesiri, iesire selectata prin
codul aplicat la cele "n" intrari de adresare.
iesiri, iesire selectata prin
codul aplicat la cele "n" intrari de adresare.
 Tabelul de functionare si
schema bloc ale demultiplexorului a carui schema logica
desfasurata este data in fig. 4.26
(inclusiv traseul cu linie intrerupta) sunt prezentate in fig.4.27.
Tabelul de functionare si
schema bloc ale demultiplexorului a carui schema logica
desfasurata este data in fig. 4.26
(inclusiv traseul cu linie intrerupta) sunt prezentate in fig.4.27.
|
INTRARI |
IESIRI |
||||||||||
|
a |
b |
c |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Din tabel
se observa ca demultiplexorul functioneaza ca un decodificator cu 8 iesiri daca la intrarea de
date ![]() se aplica semnal logic zero, deci practic
un demultiplexor poate fi folosit ca decodificator. Si reciproca este valabila, adica un decodificator poate fi
utilizat ca demultiplexor. In cazul de fata,
decodificatorul din fig.4.26 poate fi utilizat ca demultiplexor cu patru
iesiri (primele patru) daca intrarea cu ponderea cea mai mare se
considera ca fiind intrare de date.
se aplica semnal logic zero, deci practic
un demultiplexor poate fi folosit ca decodificator. Si reciproca este valabila, adica un decodificator poate fi
utilizat ca demultiplexor. In cazul de fata,
decodificatorul din fig.4.26 poate fi utilizat ca demultiplexor cu patru
iesiri (primele patru) daca intrarea cu ponderea cea mai mare se
considera ca fiind intrare de date.
Multiplexorul si demultiplexorul pot fi utilizate pentru transmiterea mai multor semnale pe o singura linie.
Circuitele decodificatoare sunt foarte utile la implementarea sistemelor de functii. Exemplu: sa se sintetizeze un circuit logic combinational care sa faca conversia din cod binar natural in cod Gray de trei variabile folosind un circuit decodificator cu 8 iesiri.
|
|
a |
b |
c |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |

5. Memoria fixa ROM
Memoriile
fixe ROM sunt circuite integrate pe scara larga avand schema bloc din
fig. 4.29 si fiind organizate sub forma unor cuvinte (in cazul nostru ![]() ) de lungime
data (pentru fig. 4.29 lungimea data este "m" biti).
) de lungime
data (pentru fig. 4.29 lungimea data este "m" biti).
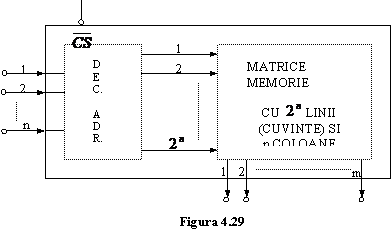
Memoria fixa are "n"
intrari de adresare, o intrare (sau mai multe) de validare (![]() ) si
"m" iesiri de date. Fiecare cuvant al memoriei este
selectat printr-o combinatie unica de valori ale variabilelor de
adresare.
) si
"m" iesiri de date. Fiecare cuvant al memoriei este
selectat printr-o combinatie unica de valori ale variabilelor de
adresare.
Cu o memorie fixa poate fi implementat un sistem de functii logice caz in care variabilele se aplica la intrarile de adresare ale memoriei, iar valoarea functiilor logice este obtinuta la iesirile memoriei. De mentionat ca fiecare functie logica este data de un bit de la iesire.
Din punct
de vedere logic o memorie cu capacitatea de ![]() cifre binare este un
selector cu "n" intrari de adresare si
cifre binare este un
selector cu "n" intrari de adresare si ![]() intrari de date reprezentate de celulele
memoriei (fig.4.30). Asa cum s-a aratat
si la prezentarea multiplexorului, o astfel de structura
realizeaza o functie logica de variabilele de adresare,
functie ale carei valori sunt specificate de intrarile de date
ale multiplexorului care, in cazul de fata, sunt impuse de
continutul celulelor de memorie.
intrari de date reprezentate de celulele
memoriei (fig.4.30). Asa cum s-a aratat
si la prezentarea multiplexorului, o astfel de structura
realizeaza o functie logica de variabilele de adresare,
functie ale carei valori sunt specificate de intrarile de date
ale multiplexorului care, in cazul de fata, sunt impuse de
continutul celulelor de memorie.
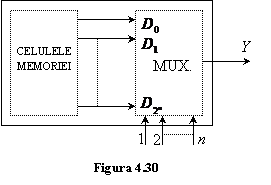
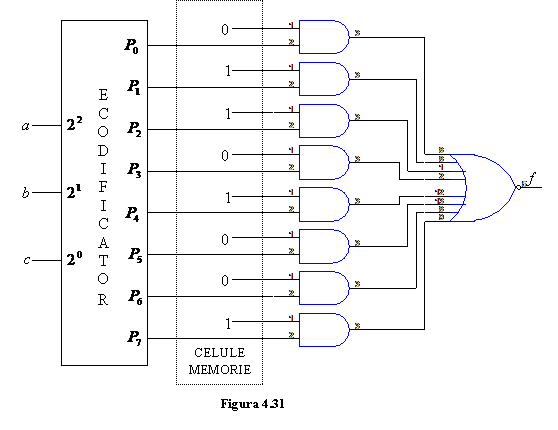
Considerand de exemplu o functie logica de trei variabile a, b, c, avand tabelul de adevar prezentat in tab.4.3, implementarea ei se poate face cu ajutorul unei memorii avand capacitatea de memorare de opt cifre binare la intrarile de adresare ale careia se
a b c f 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 Tabelul 4.3
aplica cele trei variabile: a, b si c si in care s-a inscris, la fiecare adresa, valoarea functiei corespunzatoare produsului logic standard ce corespunde adresei respective (fig.4.31).
a b c 0 0 0 0 1 0 1 0 0 1 0 0 1 1 0 1 0 0 1 1 1 0 1 1 1 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 Tabelul 4.4
![]()
![]()
![]()
![]()
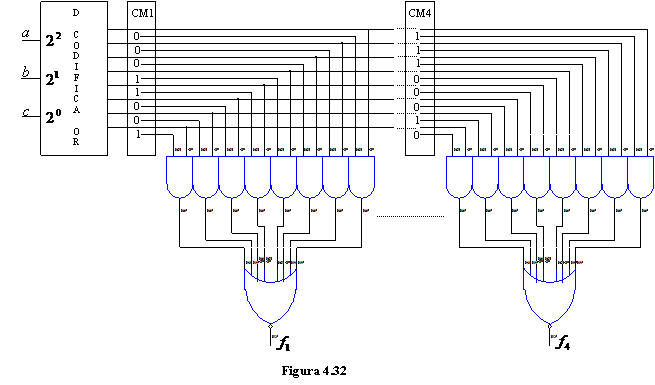
In cazul in care se urmareste implementarea unui sistem de functii logice se multiplica numarul celulelor de memorie ce sunt adresate de aceeasi iesire a decodificatorului de adresa. De exemplu in cazul in care se urmareste implementarea unui sistem de patru functii logice de trei variabile (tab.4.4) celulele de memorie se dispun matricial astfel ca o iesire a decodificatorului sa conduca la "citirea" a patru celule simultan.
De remarcat ca in cazul implementarii functiilor logice cu ajutorul memoriilor problema minimizarii acestora se pune doar in unele cazuri speciale, ce vor fi enumerate, deoarece, in mod obisnuit, in memorie se introduce chiar tabelul de definitie al functiei.
Observatie: La implementarea functiilor logice cu memorii fixe nu are importanta complexitatea functiei. Structura memoriei ce trebuie folosita este data de numarul de variabile si numarul de functii. Rezulta deci ca implementarea cu memorii fixe este recomandabila atunci cand functiile sunt complicate.
Problema care se pune la implementarea unui sistem de functii cu o memorie fixa este aceea de a folosi o memorie cat mai mica. Se cere deci sa se reduca pe cat posibil numarul variabilelor si numarul functiilor.
Reducerea numarului variabilelor de intrare este deosebit de importanta deoarece capacitatea memoriei ce trebuie utilizata se dubleaza pentru fiecare variabila de intrare. O metoda posibila de reducere a numarului de variabile consta in codificarea acestora. De exemplu 16 variabile independente ce nu se pot modifica simultan pot fi codificate cu patru variabile binare.
In mod similar numarul functiilor implementate cu o memorie fixa poate fi redus daca se foloseste un decodificator extern care sa decodifice functiile cerute din iesirile memoriei.
6. Structuri logice programabile
Structurile logice programabile sunt circuite logice combinationale capabile sa implementeze functii logice exprimate in forma normala disjunctiva. Structurile programabile contin doua matrici: o matrice de porti SI care decodifica adresa si o matrice de porti SAU care genereaza functiile logice (un SAU logic intre adresele pentru care functia ia valoarea logica 1).
Schema logica de principiu a unei structuri logice programabile cu 16 intrari si 8 iesiri avand o matrice cu 48 de porti SI cu cate 32 de intrari si o matrice cu 8 porti SAU cu cate 48 de intrari este prezentata in fig.4.33.
Structurile logice programabile se clasifica in:
a) structuri PLA atunci cand sunt programate la fabricatie prin procedee de mascare;
b) structuri FPLA in cazul in care pot fi programate de catre utilizator.
Structurile logice programabile rezolva problema codificarii variabilelor de intrare, care a fost ridicata in cazul implementarii functiilor logice cu memorii fixe, facilitand astfel implementarea unor functii logice de un numar foarte mare de variabile. Astfel, spre deosebire de memorii unde se decodifica toate adresele posibile, in cazul structurilor programabile sunt decodificate numai adresele utilizate (produsele logice pentru care functia ia valoarea logica 1). Adresele utilizate sunt specificate in formularul de programare. Pentru exemplificare, in tabelul 4.5 si in fig.4.34 sunt date formularul de programare si schema logica simplificata a unei structuri logice cu 4 intrari si 4 iesiri care realizeaza conversia din cod zecimal codificat binar in cod Gray.

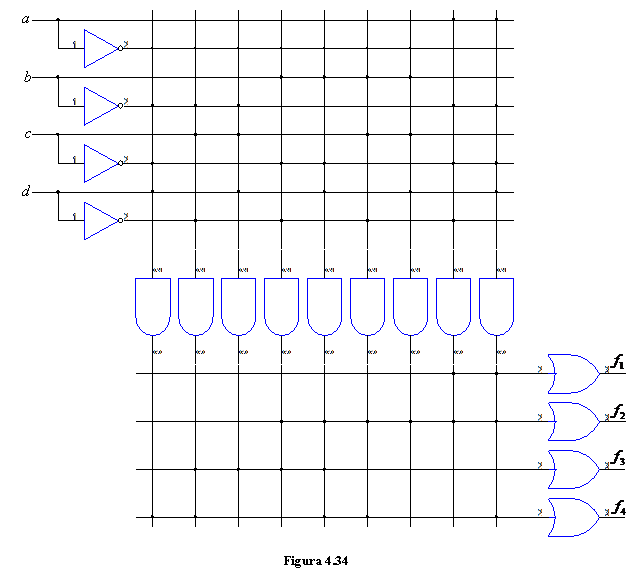
NR. ADRESA INTRARI IESIRI a b c d 1 0 0 0 0 0 0 0 0 2 0 0 0 1 0 0 0 1 3 0 0 1 0 0 0 1 1 4 0 0 1 1 0 0 1 0 5 0 1 0 0 0 1 1 0 6 0 1 0 1 0 1 1 1 7 0 1 1 0 0 1 0 1 8 0 1 1 1 0 1 0 0 9 1 0 0 0 1 1 0 0 10 1 0 0 1 1 1 0 1 Tabelul 4.5
![]()
![]()
![]()
![]()
Structura are in componenta
sa o matrice cu 9 porti SI a cate 8 intrari
si 4 porti SAU cu cate 9 intrari. Cele patru
functii ![]() si
si ![]() se obtin ca sume de produse logice.
se obtin ca sume de produse logice.
La implementarea functiilor logice cu structuri programabile se pot folosi toate metodele de minimizare cunoscute. In practica insa minimizarea nu este necesara decat atunci cand, in forma canonica, numarul de produse logice standard este mai mare decat numarul adreselor disponibile in structura programabila. Minimizarea are sens numai in cazul in care se reuseste implementarea functiilor logice cerute cu o structura programabila de dimensiuni mai mici, avand in vedere ca aceste structuri se produc in variante care difera prin numarul de intrari, numarul de iesiri si numarul de adrese (cuvinte). Cum, pentru o aplicatie data, numarul de intrari si de iesiri este dat, rezulta ca reducerea ce se poate obtine vizeaza numarul adreselor.
Pentru exemplul dat, cel al unui convertor din cod zecimal codificat binar in cod Gray se obtine urmatorul formular de programare si structura din fig. 4.35.
NR. ADRESA INTRARI IESIRI a b c d 1 1 * * * 1 1 0 0 2 * 1 * * 0 1 0 0 3 * 1 0 * 0 1 1 0 4 * 0 1 * 0 0 1 0 5 * * 1 0 0 0 0 1 6 * * 0 1 0 0 0 1 Tabelul 4.6
![]()
![]()
![]()
![]()
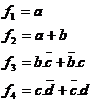
S-a obtinut o structura cu 6 adrese. Mai trebuie mentionat si faptul ca daca pentru implementare s-ar fi folosit o memorie fixa, ar fi fost utilizate 16 adrese corespunzatoare celor 16 combinatii posibil de realizat cu cele patru variabile de intrare.
7. Aplicatii ale circuitelor logice combinationale. Sumatorul
Sumatorul
se defineste ca fiind circuitul logic combinational care
asigura, direct sau indirect, efectuarea insumarii a doua numere
binare tinand cont de un eventual transport
initial. In fig. 4.39 este prezentat modul de reprezentare a unui sumator
pe "n" biti care tine cont de un eventual transport initial ![]() si genereaza, daca este cazul,
un transport final
si genereaza, daca este cazul,
un transport final ![]() .
.

Circuitul
logic combinational care asigura, direct sau indirect, insumarea a
doua numere binare cu cate un bit fara a lua in considerare
transportul de la bitul cu ponderea imediat inferioara este denumit
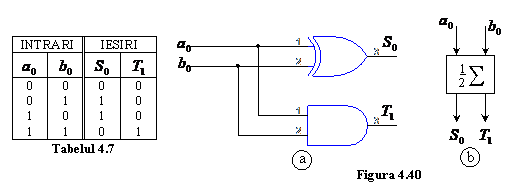
semisumator. Tabelul de adevar al unui semisumator la intrarea caruia
se aplica doua numere binare de cate un bit, ![]() si respectiv
si respectiv ![]() , este
prezentat in tab.4.7.
, este
prezentat in tab.4.7.
Din tabel
rezulta urmatoarele expresii pentru variabilele de iesire
suma (![]() ) si
transport catre bitul de rang imediat superior
) si
transport catre bitul de rang imediat superior ![]()
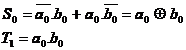 (4.1)
(4.1)
expresii ce sunt implementate de schema logica din fig.4.40a. Reprezentarea simbolica a acestei scheme este redata in fig.4.40b.
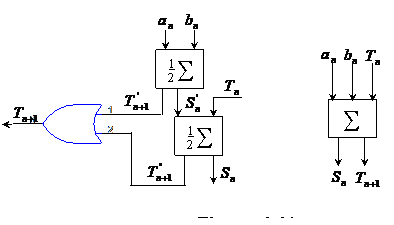
In
principiu, sumatorul complet pentru un bit oarecare de rangul n se poate realiza utilizand doua
semisumatoare conform schemei din fig.4.41, unde cu ![]() s-a notat transportul de la bitul de rang
imediat inferior, iar cu
s-a notat transportul de la bitul de rang
imediat inferior, iar cu ![]() transportul catre bitul de rang imediat
superior. Primul semisumator efectueaza o suma partiala
transportul catre bitul de rang imediat
superior. Primul semisumator efectueaza o suma partiala ![]() si un transport partial
si un transport partial ![]() in timp ce al doilea, tinand cont de transportul
in timp ce al doilea, tinand cont de transportul ![]() ,
genereaza suma
,
genereaza suma ![]() si transportul
si transportul ![]() . De remarcat ca
. De remarcat ca ![]() si
si ![]() nu pot fi simultan egale cu 1.
nu pot fi simultan egale cu 1.
In practica insa nu se foloseste aceasta solutie, ci se pleaca de la tabelul de adevar al unui sumator, expresiile variabilelor de iesire minimizandu-se cu una din metodele cunoscute (tabelul 4.8).
0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 Tabelul 4.8
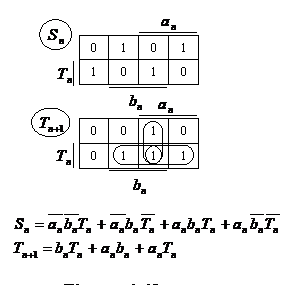
![]()
![]()
![]()
![]()
![]()
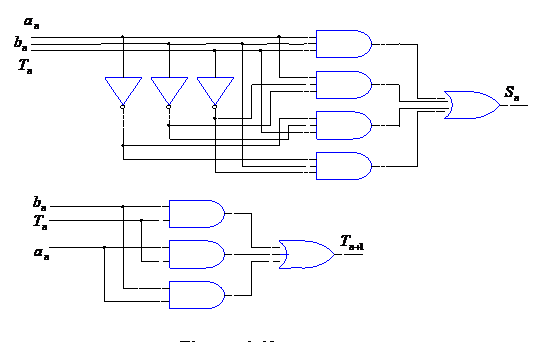
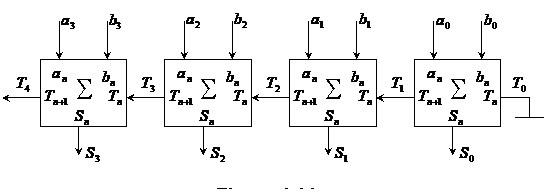
Schemele combinationale care implementeaza acest sumator sunt date in fig.4.43.In figura 4.44 este data schema unui sumator multibit obtinut prin interconectarea mai multor sumatoare.Propagarea transportului este de tip serie.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |