TRIUNGHIUL - Test 1
Calculati perimetrul unui triunghi ABC, cand:
a)AB=0,5 dam; BC=30 dm; AC=4,2m
b)AB=4 cm, BC este de doua ori mai mare decat AB, AC este cu 2 cm mai mica decat BC.
c)AB=10 m, BC este de doua ori mai mica decat AB, AC este cu 2.500 mm mai mare decat BC.
d)AB=36 dm, BC este ![]() din AB, AC este
din AB, AC este ![]() din suma primelor
doua laturi.
din suma primelor
doua laturi.
Sa se afle lungimile
laturilor unui triunghi avand perimetrul de 90 dm, stiind ca lungimea
primei laturi este ![]() din lungimea celei
de-a doua, iar a celei de a treia este
din lungimea celei
de-a doua, iar a celei de a treia este ![]() din lungimea primei.
din lungimea primei.
Lungimile laturilor unui triunghi sunt direct proportionale cu 3, 5 si 7, iar perimetrul sau este 360 cm. Aflati lungimile acestor laturi.
Sa se determine perimetrul unui triunghi isoscel, stiind ca lungimea laturilor congruente este cu 24 cm mai mare decat lungimea bazei, iar raportul dintre cele doua lungimi este 2,(3).
Calculati perimetrul unui triunghi isoscel cunoscand doua laturi de lungimi 10, respectiv 8 cm.
Sa se afle laturile unui triunghi ABC, stiind ca perimetrul lui este de 39 cm si lungimea laturii AC reprezinta 80% din lungimea laturii AB, iar lungimea laturii BC reprezinta120% din lungimea laturii AB.
Sa se determine masurile unghiurilor exterioare triunghiului ABC, stiind ca:
![]() ,
, ![]() si
si ![]() .
.
Sa se construiasca
triunghiul ABC in fiecare din cazurile: a)AB=BC=4 cm si ![]()
b)AC=5 cm, ![]() si
si ![]() c)AB=3 cm, BC=5 cm si AC=6 cm
c)AB=3 cm, BC=5 cm si AC=6 cm
d)AB=1,5 cm, BC=2 cm si
AC=2,5 cm e) AB=3 cm, BC=4 cm si ![]()
f) AB=5 cm, ![]() si
si ![]() g)AB=BC=AC=3 cm
g)AB=BC=AC=3 cm
Clasificati triunghiurile construite la problema anterioara dupa:a)laturi b)unghiuri
Sa se construiasca
un triunghi ABC cu AB=6 cm si ![]() , daca:a)BC=4
cm b)BC=3
cm
, daca:a)BC=4
cm b)BC=3
cm
Sa se arate ca triunghiurile ABC si EFD sunt congruente in urmatoarele situatii si sa se scrie si celelalte elemente congruente:
a)AB=EF, AC=DE, ![]() b)AC=DE, AB=EF, BC=DF
b)AC=DE, AB=EF, BC=DF
c)BC=DF, ![]() ,
, ![]() d)
d)![]() ,
, ![]() , BA=EF
, BA=EF
Daca AC=PM=3 cm,
AB=MN=2,5 cm, iar ![]() =1200, sa se arate ca cele doua
triunghiuri sunt congruente si sa se scrie toate celelalte elemente
congruente ale triunghiurilor.
=1200, sa se arate ca cele doua
triunghiuri sunt congruente si sa se scrie toate celelalte elemente
congruente ale triunghiurilor.
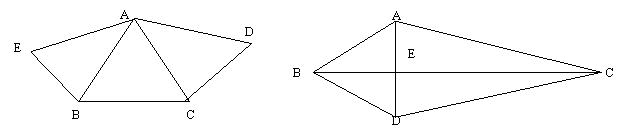 Daca
triunghiul ABC este isoscel cu [AB]s[AC],
Daca
triunghiul ABC este isoscel cu [AB]s[AC], ![]() si [BE] si
[AD], atunci triunghiul ABE este congruent cu triunghiul CAD. Sa se scrie
toate celelalte elmente congruente ale triunghiului.(fig.1)
si [BE] si
[AD], atunci triunghiul ABE este congruent cu triunghiul CAD. Sa se scrie
toate celelalte elmente congruente ale triunghiului.(fig.1)
fig.1 fig.2
Daca [AB]s[BD] si ABCsDBC, atunci:a)DABC=DDBC b)DABE=DDBE c)DACE=DDCE (fig.2)
Pe laturile unghiului XOY se considera punctele AI(OX, BI(OX, CI(OY si DI(OY astfel incat OA=3 cm, OB=5 cm, OC=3 cm si OD=5 cm. Sa se arate ca triunghiurile OAD si OCB sunt congruente.
Fie triunghiurile ABC
si MNP. AB=MP=2,5 cm, ![]() =600 si
=600 si ![]() =700. Sa se arate ca cale doua
triunghiuri sunt congruente si sa se scrie celelalte elemente
congruente ale lor.
=700. Sa se arate ca cale doua
triunghiuri sunt congruente si sa se scrie celelalte elemente
congruente ale lor.
Daca in figura de mai
jos ![]() si
si ![]() , atunci triunghiul ABD este congruent cu triunghiul CDB.
Sa se scrie celelalte elemente congruente ale triunghiurilor. (fig.3)
, atunci triunghiul ABD este congruent cu triunghiul CDB.
Sa se scrie celelalte elemente congruente ale triunghiurilor. (fig.3)

fig.3 fig.4 fig.5
Triunghiul ABC este isoscel
cu [AB]s[AC], ![]() =900 si
=900 si ![]() , atunci triunghiurile APB si AQC sunt congruente.
Sa se scrie celelalte elemente congruente ale triunghiului. (fig.4)
, atunci triunghiurile APB si AQC sunt congruente.
Sa se scrie celelalte elemente congruente ale triunghiului. (fig.4)
Daca in figura de mai jos [OM este bisectoarea unghiului AOB, atunci AM=MB. (fig.5)
 In
figura de mai jos triunghiul ABC este isoscel cu AB=AC, AN=AM, iar
In
figura de mai jos triunghiul ABC este isoscel cu AB=AC, AN=AM, iar ![]() , atunci BN=MC. (fig.6)
, atunci BN=MC. (fig.6)
fig.6 fig.7 fig.8
Daca in figura de mai sus AO=OC si DO=OB, atunci: (fig.7)
a)AD=BC b)AB=DC c)![]() d)
d)![]()
In figura de mai jos AC=BC, ![]() si
si ![]() . Aratati ca:
. Aratati ca:
a)AE=BF si ![]() b)EC=FD si
b)EC=FD si ![]() c)EB=FA si
c)EB=FA si ![]()
Se dau punctele C si D
de o parte si de alta a unei drepte d si punctele A a, BId, astfel incat CA=AD
si CB=BD. Demonstrati ca ![]() .
.
Daca in figura de mai
sus EA=CP, ED=BP si ![]() , atunci: (fig.8)
, atunci: (fig.8)
a)AD=BC si ![]() b)AB=DC c)EC=AP si
b)AB=DC c)EC=AP si ![]()
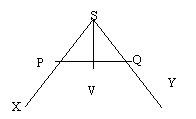 In
figura de mai jos
In
figura de mai jos ![]() , SP=SQ si
, SP=SQ si ![]() . Sa se arate ca
. Sa se arate ca
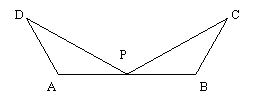 Daca
in figura de mai jos AP=BP,
Daca
in figura de mai jos AP=BP,
![]() si
si ![]() , atunci: (fig.10)
, atunci: (fig.10)
a)AD=BC si DP=CP
b)BD=AC si ![]()
In figura de mai jos ![]() fig.9
fig.10
fig.9
fig.10
si ![]() . Aratati ca
. Aratati ca ![]() si XM=XN.
si XM=XN.
Triunghiurile ABC si MNP sunt congruente si triunghiurile C'A'B' si ABC sunt congruente. Scrieti congruentele care rezulta din cele doua relatii de congruenta. Desenati figurile.
Triunghiurile ABM si
ABN sunt congruente, ![]() =900. Calculati
=900. Calculati ![]() . Contine AB bisectoarea
. Contine AB bisectoarea ![]() ?Justificati si prin desen.
?Justificati si prin desen.
Triunghiurile ABC si
MNP sunt congruente, AC=5 cm si ![]() =400. Care este lungimea segmentului [MN] si
masura unghiului ACB, daca [AB]s[NP] si [BC]s[PM]?
=400. Care este lungimea segmentului [MN] si
masura unghiului ACB, daca [AB]s[NP] si [BC]s[PM]?
Un triunghi echilateral are semiperimetrul de 24 cm. Aflati latura lui.
Lungimile laturilor unui triunghi sunt direct proportionale cu 5, 6 si 7. Aflati masurile lor stiind ca perimetrul triunghiului este de 36 cm.
Fie unghiul ROD si bisectoarea sa [OM. Daca unghiul dintre dreptele OM si RD este de 900, stabiliti ce fel de triunghi este triunghiul ROD.
Fie M mijlocul bazei triunghiului isoscel ABC (AB=AC). Aratati ca (AM este bisectoarea unghiului BAC.
In triunghiul ABC, DI[BC] astfel incat [AD]s[CD]. Daca perimetrul triunghiului ABC este de 25 cm, sa se afle latura AC.
Se da triunghiul isoscel ABC, [AB]s[AC]. Se iau punctele DI(AB) si EI(AC) astfel incat AD=DB si AE=EC. Sa se demonstreze ca [BE]s[CD].
In exteriorul triunghiului oarecare ascutit unghic MNP sunt construite triunghiurile echilaterale MNQ si MPR. Cercetati daca [QP]s[NR].
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |