
In cele ce urmeaza se intentioneaza revederea succinta a principalelor operatiuni din algebra si analiza vectoriala, strict necesare in tratarea atat teoretica cat si sub aspect aplicativ a problematicii care face obiectul de studiu al Mecanicii. Se are in vedere o anumita rigurozitate in precizarea unor aspecte de detaliu, necesara in special la elaborarea algoritmelor de calcul programabile.
1 Marimi scalare si marimi vectoriale
Pentru caracterizarea unei marimi scalare este suficienta o determinare cantitativa printr-un numar real de unitati de masura. Simbolizarea unei marimi scalare este alfanumerica. Se includ in aceasta categorie lungimea unui segment (l), masa (m), timpul (t), lucrul mecanic (L), energia cinetica (E) si potentiala (V), momentul de inertie mecanic (J), etc.
Atributele unei marimi
vectoriale sunt modulul, directia sisensul de actiune. In Mecanica, pe langa
simbolizarea cunoscuta ![]() se utilizeaza mai
frecvent o simbolizare, devenita traditionala, constand dintr-o
bara asezata deasupra notatiei alfanumerice a marimii
respective (
se utilizeaza mai
frecvent o simbolizare, devenita traditionala, constand dintr-o
bara asezata deasupra notatiei alfanumerice a marimii
respective (![]() ), neexistand posibilitatea unor confuzii. Cateva exemple de
marimi vectoriale sunt: forta
(
), neexistand posibilitatea unor confuzii. Cateva exemple de
marimi vectoriale sunt: forta
(![]() ), momentul fortei fata de un punct (
), momentul fortei fata de un punct (![]() ), vectorul de
pozitie (
), vectorul de
pozitie (![]() ), viteza (
), viteza (![]() ) si acceleratia (
) si acceleratia (![]() ) ale unui punct, viteza
unghiulara (
) ale unui punct, viteza
unghiulara (![]() ) si acceleratia unghiulara (
) si acceleratia unghiulara (![]() ) ale unui corp, impulsul
(
) ale unui corp, impulsul
(![]() ) si momentul cinetic (
) si momentul cinetic (![]() ), etc. Elementele de grafica caracteristice unui vector
oarecare
), etc. Elementele de grafica caracteristice unui vector
oarecare ![]() sunt reprezentate in
fig. 1.
sunt reprezentate in
fig. 1.
|
Fig.1 |
Modulul
vectorului, notat ![]() , este un scalar pozitiv si caracterizeaza dimensional marimea vectoriala
respectiva. Directia vectorului
este reprezentata prin dreapta suport coliniara cu vectorul continand,
evident, si punctul de aplicatie
A al acestuia; pe aceasta dreapta sensul pozitiv se atribuie
prin versorul
, este un scalar pozitiv si caracterizeaza dimensional marimea vectoriala
respectiva. Directia vectorului
este reprezentata prin dreapta suport coliniara cu vectorul continand,
evident, si punctul de aplicatie
A al acestuia; pe aceasta dreapta sensul pozitiv se atribuie
prin versorul ![]() atasat.
atasat.
Pozitia
dreptei suport si, implicit, cea
a vectorului in raport cu o directie fixa de referinta (de
obicei axa Ox) se indica prin unghiul de pozitie ![]() dintre sensurile
pozitive ale acestor directii; unghiul de pozitie este un unghi
orientat, pozitiv in sens trigonometric. Sensul
vectorului se raporteaza la versorul
dintre sensurile
pozitive ale acestor directii; unghiul de pozitie este un unghi
orientat, pozitiv in sens trigonometric. Sensul
vectorului se raporteaza la versorul ![]() ; un vector
; un vector ![]() va avea sens contrar
lui
va avea sens contrar
lui ![]() .
.
2 Definiri grafo-analitice ale vectorilor
Operatiunile cu marimi vectoriale pot fi mai usor urmarite, atat in tratarea teoretica cat si in aplicatii, apeland la reprezentari grafice, nefiind obligatorie insa desenarea la scara a vectorilor.
1 Proiectia unui vector pe o axa
Se
considera o dreapta oarecare ![]() si un vector
si un vector ![]() necoplanar cu aceasta
(fig. 2). Prin punctul A de aplicatie
al vectorului se construieste dreapta
necoplanar cu aceasta
(fig. 2). Prin punctul A de aplicatie
al vectorului se construieste dreapta ![]() iar din varful B se duce
iar din varful B se duce ![]() . Se duc apoi perpendicularele comune AA1 si B'B1. Lungimea segmentului A1B1, notata
. Se duc apoi perpendicularele comune AA1 si B'B1. Lungimea segmentului A1B1, notata ![]() , reprezinta proiectia vectorului
, reprezinta proiectia vectorului ![]() pe directia
pe directia ![]() . Astfel:
. Astfel:
![]() (1)
(1)
in
care ![]() si
si ![]() .
.
|
Fig.2 |
Se
remarca faptul ca proiectia oricarui vector pe o dreapta
este o marime scalara si
se obtine inmultind scalar vectorul respectiv cu versorul directiei
pe care se face proiectarea. Semnul proiectiei depinde de unghiul de pozitie
![]() al vectorului cu
al vectorului cu ![]() . Astfel, daca
. Astfel, daca ![]() ,
, ![]() iar pentru
iar pentru ![]() ,
, ![]() . Proiectia este nula in cazul unui vector
perpendicular pe
. Proiectia este nula in cazul unui vector
perpendicular pe ![]() (fig.3). Un vector se
proiecteaza in adevarata marime pe propria lui directie
de actiune sau pe o paralela la aceasta. In acest caz, daca
(fig.3). Un vector se
proiecteaza in adevarata marime pe propria lui directie
de actiune sau pe o paralela la aceasta. In acest caz, daca ![]() este versorul directiei
vectorului (fig. 1), se poate scrie:
este versorul directiei
vectorului (fig. 1), se poate scrie:
![]() (2)
(2)
deoarece
![]() . Proiectia
. Proiectia ![]() este negativa daca
este negativa daca
![]() si
si ![]() au sensuri opuse,
respectiv in cazul unui vector
au sensuri opuse,
respectiv in cazul unui vector ![]() .
.
|
Fig.3 |
2 Proiectii pe axele de coordonate
In
raport cu un sistem de referinta cartezian directia unui vector
este determinata prin unghiurile directoare ![]() formate de dreapta suport a vectorului cu axele de coordonate
(fig. 4).
formate de dreapta suport a vectorului cu axele de coordonate
(fig. 4).
|
Fig. 4 |
Proiectiile
unui vector ![]() pe aceste axe vor fi
date de relatiile
pe aceste axe vor fi
date de relatiile
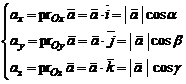 (3)
(3)
in
care ![]() sunt versorii axelor
de coordonate. Intre unghiurile directoare exista relatia:
sunt versorii axelor
de coordonate. Intre unghiurile directoare exista relatia:
![]() (4)
(4)
|
Fig. 4 |
in baza careia se poate scrie:
![]() (5)
(5)
Daca
in locul unghiurilor directoare directia vectorului se defineste prin
unghiurile ![]() si
si ![]() (fig.5), proiectiile
vectorului
(fig.5), proiectiile
vectorului ![]() pe axele de coordonate
se pot calcula cu relatiile:
pe axele de coordonate
se pot calcula cu relatiile:
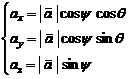 (6)
(6)
3 Expresia analitica a unui vector
|
Fig. 6 |
Un vector oarecare poate fi descompus dupa trei directii care nu sunt coplanare. In fig. 6 este ilustrata situatia in care aceste directii sunt paralele cu axele de coordonate. In baza regulii para lelogramului se poate scrie
![]() (7)
(7)
Vectorii
![]() reprezinta componentele
vectorului
reprezinta componentele
vectorului ![]() dupa directiile
axelor de coordonate. Aceste componente se proiecteaza fiecare pe cate o
axa in adevarata marime, ceea ce rezulta fiind tocmai
dupa directiile
axelor de coordonate. Aceste componente se proiecteaza fiecare pe cate o
axa in adevarata marime, ceea ce rezulta fiind tocmai ![]() , respectiv proiectiile
vectorului
, respectiv proiectiile
vectorului ![]() .
.
Legatura
intre proiectii si
componente se face prin intermediul versorilor ![]() , in baza relatiei (2):
, in baza relatiei (2):
![]() (7')
(7')
Inlocuind in (7) se obtine
![]() (8)
(8)
|
Fig. 7 |
relatie
care defineste analitic vectorul ![]() . Inlocuind in cele de mai sus vectorul
. Inlocuind in cele de mai sus vectorul ![]() prin versorul
prin versorul ![]() se constata cu usurinta
ca proiectiile pe axe ale versorului sunt tocmai cosinusurile sale
directoare:
se constata cu usurinta
ca proiectiile pe axe ale versorului sunt tocmai cosinusurile sale
directoare:
![]() (9)
(9)
Daca
un vector este continut intr-un plan, de exemplu in xOy (fig. 7), atunci ![]() si relatiile de mai sus iau forma
simplificata
si relatiile de mai sus iau forma
simplificata
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Mentionam
ca relatiile (3), (6) si (10) mai pot fi scrise inlocuind ![]() prin proiectia a. O astfel de scriere a proiectiilor este necesara atunci cand pentru acel
vector este cunoscuta numai directia de actiune, marimea si
sensul urmand sa rezulte din calcule. O valoare negativa pentru a arata ca sensul de actiune
al vectorului este invers celui considerat initial.
prin proiectia a. O astfel de scriere a proiectiilor este necesara atunci cand pentru acel
vector este cunoscuta numai directia de actiune, marimea si
sensul urmand sa rezulte din calcule. O valoare negativa pentru a arata ca sensul de actiune
al vectorului este invers celui considerat initial.
3 Operatiuni elementare cu vectori concurenti
In cazul unor vectori concurenti reprezentand marimi fizice de aceeasi natura (ca de exemplu un sistem de forte actionand simultan asupra unui punct material) se pune problema reducerii acestora, respectiv a gasirii unui singur vector rezultant, echivalent ca efect sistemului de vectori dat. Se determina atributelor vectorului rezultant, respectiv modulul, directia si sensul acestuia.
|
Fig. 8 |
Suma
![]() urmeaza regula paralelo-gramului (fig. 8)
conform careia vectorul rezultant are marimea si directia
diagonalei paralelogramului construit cu cei doi vectori ca laturi. Este usor
de constatat geometric ca:
urmeaza regula paralelo-gramului (fig. 8)
conform careia vectorul rezultant are marimea si directia
diagonalei paralelogramului construit cu cei doi vectori ca laturi. Este usor
de constatat geometric ca:
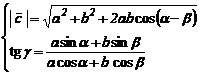 (13)
(13)
Diferenta ![]() urmeaza aceeasi
regula (fig. 9), relatiile de calcul devenind
urmeaza aceeasi
regula (fig. 9), relatiile de calcul devenind
|
Fig. 9 |
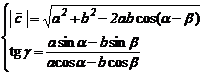 (14)
(14)
Vectorul
![]() poate fi reprezentat si prin unirea varfurilor
vectorilor
poate fi reprezentat si prin unirea varfurilor
vectorilor ![]() si
si ![]() in modul aratat
in fig. 9.
in modul aratat
in fig. 9.
In cazul unui sistem format din mai mult de doi vectori, pentru gasirea rezultantei se poate aplica succesiv regula paralelogramului. Mai eficienta este in acest caz regula poligonului care consta in construirea unei linii poligonale (plana sau tridimensionala) ale carei laturi sunt construite din vectori paraleli si egali cu cei ai sistemului dat; vectorul rezultant uneste punctul de aplicatie al primului vector al poligonului cu varful ultimului. In fig.10 s-a exemplificat metoda pentru cazul a trei vectori coplanari.
In cazul a n vectori concurenti vectorul rezultant este:
![]() (15)
(15)
Se
inmulteste scalar aceasta relatie cu ![]() versorul unei axe
versorul unei axe ![]() oarecare
oarecare
![]()
In baza relatiei (1) se poate scrie:
![]() (16)
(16)
Aceasta relatie exprima teorema proiectiilor care se enunta astfel: proiectia pe o axa a rezultantei unui sistem de vectori concurenti este egala cu suma proiectiilor acestor vectori pe axa respectiva.
Aplicand aceasta teorema relativ la axele de coordonate se obtine:
|
Fig. 10 |
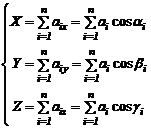 (17)
(17)
Vectorul rezultantei
![]() (18)
(18)
are modulul si unghiurile directoare date de relatiile:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
iar pentru vectorul rezultant se poare scrie
![]() (22)
(22)
4 Inmultiri vectoriale
4.1 Inmultirea unui vector cu un scalar
|
Fig. 11 |
Prin inmultirea unui vector cu un scalar se obtine un vector coliniar cu acesta (fig.11):
![]() (23)
(23)
Daca
![]() si
si ![]() reprezinta marimi
avand aceeasi natura fizica,
de exemplu doua forte, atunci scalarul l
este un factor de amplificare adimensional; daca sunt diferite, de exemplu
o forta si un moment, atunci l este un factor de transformare a carui
unitate de masura depinde de natura marimilor respective. Daca
l < 0, atunci
reprezinta marimi
avand aceeasi natura fizica,
de exemplu doua forte, atunci scalarul l
este un factor de amplificare adimensional; daca sunt diferite, de exemplu
o forta si un moment, atunci l este un factor de transformare a carui
unitate de masura depinde de natura marimilor respective. Daca
l < 0, atunci ![]() si
si ![]() au sensuri opuse. Cu exprimarile analitice
au sensuri opuse. Cu exprimarile analitice
![]() (24)
(24)
este evidenta relatia:
![]() (25)
(25)
care exprima faptul ca intre proiectiile pe axe ale vectorilor coliniari exista acelasi raport de proportionalitate. Aceasta observatie va fi necesara in Statica la stabilirea ecuatiei axei centrale a unui sistem de forte paralele. Relatia (2) confirma totodata si legatura dintre un vector si versorul directiei pe care se afla.
|
Fig. 12 |
4.2 Produsul scalar
Inmultirea scalara dintre
doi vectori ![]() si
si ![]() se exprima prin
relatia:
se exprima prin
relatia:
![]() (26)
(26)
in
care ![]() este unghiul dintere
cei doi vectori (fig.12). Pentru
este unghiul dintere
cei doi vectori (fig.12). Pentru ![]() , unde
, unde ![]() , produsul scalar ia forma:
, produsul scalar ia forma:
![]() (27)
(27)
Produsul scalar este comutativ si distributiv fata de adunare, respectiv:
Produsul scalar este nul in cazul in care cei doi vectori sunt perpendiculari unul pe celalalt. Inmultind scalar un vector cu el insusi se obtine:
![]() (29)
(29)
![]() (30)
(30)
Daca vectori sunt exprimati analitic, atunci inmultirea scalara ia forma
![]() (31)
(31)
Vom intalni produsul scalar in Statica la reducerea sistemelor de forte si in Dinamica la calculul lucrului mecanic al unei forte.
|
Fig. 13 |
4.3 Produsul vectorial
Considerand
aceiasi vectori ![]() si
si ![]() (fig. 13), produsul
vectorial se exprima prin relatia:
(fig. 13), produsul
vectorial se exprima prin relatia:
![]() (32)
(32)
![]() (33)
(33)
Directia
acestui vector este perpendiculara pe directiile vectorilor ![]() si
si ![]() , deci pe planul in care sunt continuti acestia.
Sensul vectorului
, deci pe planul in care sunt continuti acestia.
Sensul vectorului ![]() se determina
aplicand regula surubului drept. Astfel, un surub drept rotit in
sensul de la
se determina
aplicand regula surubului drept. Astfel, un surub drept rotit in
sensul de la ![]() catre
catre ![]() , acoperind unghiul a
, va avansa in sensul lui
, acoperind unghiul a
, va avansa in sensul lui ![]() .
.
Produsul vectorial nu este comutativ:
![]() (34)
(34)
![]() (35)
(35)
Un scalar care inmulteste un produs vectorial poate fi atasat oricaruia dintre cei doi vectori:
![]() (36)
(36)
Rezultatul inmultirii unui vector cu el insusi este nul:
![]() (37)
(37)
Produsele dintre versori vor avea urmatoarele rezultate:
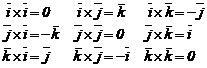 (38)
(38)
Daca
![]() si
si ![]() sunt exprimati analitic atunci
sunt exprimati analitic atunci
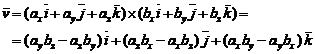 (39)
(39)
Se verifica usor ca aceste relatii reprezinta dezvoltarea unui determinant:
![]()
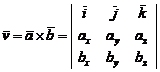 (40)
(40)
dupa versorii din prima linie. Vom intalni produsul vectorial in Statica la calculul momentului unei forte in raport cu un punct, in Cinematica la calculul vitezei si acceleratiei in miscarea de rotatie, in Dinamica la calculul momentului cinetic.
4.4 Produsul mixt
Cu
trei vectori ![]() si
si ![]() se poate forma un
produs mixt de forma:
se poate forma un
produs mixt de forma:
![]() (41)
(41)
avand ca rezultat o marime scalara. Acest produs nu este comutativ, astfel ca rocada intre doi dintre vectorii produsului modifica semnul rezultatului:
![]() (42)
(42)
![]() (43)
(43)
deoarece
![]() este perpendicular pe
planul vectorilor
este perpendicular pe
planul vectorilor ![]() si
si ![]() si deci si pe
si deci si pe ![]() . Produsul mixt mai este nul daca doi dintre vectori
sunt coliniari sau paraleli; considerand, de exemplu, coliniari vectorii
. Produsul mixt mai este nul daca doi dintre vectori
sunt coliniari sau paraleli; considerand, de exemplu, coliniari vectorii ![]() si
si ![]() se poate scrie
se poate scrie ![]() si, tinand
cont de (37), va rezulta:
si, tinand
cont de (37), va rezulta:
![]() (44)
(44)
Daca
![]() ,
, ![]() si
si ![]() sunt exprimati
analitic, produsul mixt se poate pune
sub forma unui determinant:
sunt exprimati
analitic, produsul mixt se poate pune
sub forma unui determinant:
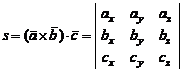 (45)
(45)
Rezultatul produsului mixt va fi egal cu valoarea determinantului.
Vom intalni produsul mixt in Statica la calculul momentelor fata de axe ca si in unele demonstratii.
4.5 Produsul vectorial dublu
Cu
vectorii ![]() ,
, ![]() si
si ![]() se poate forma un
produs vectorial dublu de forma:
se poate forma un
produs vectorial dublu de forma:
![]() (46)
(46)
avand ca rezultat un vector. Acest produs mai poate fi pus si sub forma:
![]() (47)
(47)
Produsul dublu vectorial se utilizeaza in Cinematica la calculul accelera-tiilor unui solid rigid.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |