Problema care se formuleaza este de determinare a minimului pentru o functie reala f care depinde de mai multe variabile.
Utilizand rationamentul din subparagraful 3.2.1, aplicat unui vector de n componente, x de n componente x1, x2,., xn se pot deduce conditiile de minim local, respectiv global.
Un vector x*=[x*1 x*2 . x*n]T, din An se numeste minim local al functiei f daca exista un e>0, suficient de mic, astfel incat pentru oricare vector x aflat intr-o vecinatate a lui x*, adica:
![]() (3.28)
(3.28)
f(x*) nu depaseste valoarea lui f(x):
![]() (3.29)
(3.29)
Un vector x* din An se numeste minim global (absolut) al functiei f daca
![]() (3.30)
(3.30)
pentru toti x din An
Fie domeniul D o submultime
deschisa si marginita din An. Se
noteaza granita domeniului D prin ![]() , domeniul inchis
, domeniul inchis
![]() si se considera
si se considera ![]() o submultime a lui An astfel incat
o submultime a lui An astfel incat ![]() . Un punct x* din
. Un punct x* din ![]() se considera minimul functiei f din
se considera minimul functiei f din ![]() , f(x)=f(x1,
x2,, xn) continua pe
, f(x)=f(x1,
x2,, xn) continua pe ![]() , daca
exista un e>0,
suficient de mic, astfel incat pentru oricare vector x aflat intr-o vecinatate a lui x*, adica x
apartine sferei S cu centrul in x* si de raza e
, daca
exista un e>0,
suficient de mic, astfel incat pentru oricare vector x aflat intr-o vecinatate a lui x*, adica x
apartine sferei S cu centrul in x* si de raza e
![]() (3.31)
(3.31)
are loc inegalitatea:
![]() (3.32)
(3.32)
Se presupune ca derivatele partiale in raport cu fiecare componenta a vectorului x sunt continue pe D.
Conditia necesara de minim local a unei functii f in punctul x* din D este consta in anularea tuturor derivatelor partiale ale functiei f in punctul x*:
![]() (3.33)
(3.33)
Practic, relatia (3.33) reprezinta conditia de anulare a gradientului functiei f in punctul x*.
Conditia suficienta: Daca gradientul functiei f este vectorul nul si daca matricea simetrica Q, de dimensiune n n, este pozitiv definita:
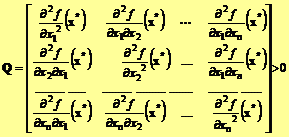 (3.34)
(3.34)
atunci x* este minimul functiei f.
Observatie - Fie Q o matrice simetrica de dimensiune 3 3:
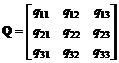 (3.35)
(3.35)
Matricea Q este pozitiv definita daca si numai daca:
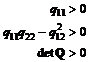 (3.36)
(3.36)
Exemplul 1
Fie o functie definita pe A2
![]() (3.37)
(3.37)
Sa se determine minimul functiei f(x,y).
Rezolvare
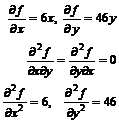 (3.38)
(3.38)
Din conditia de necesitate (3.33), aplicata functiei f(x,y), rezulta x=0, y=0. Deci, minimul functiei f(x,y) este (0,0).
Din conditia de suficienta (3.34), aplicata functiei f(x,y), rezulta matricea Q de forma:
![]() ,(3.39)
,(3.39)
a carui determinant este 276 fiind mai mare decat zero.
In concluzie, originea este minimul functiei date.
Concluzii
Daca f este o functie definita pe A3, atunci matrice Q este de forma:
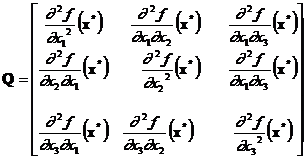
Din conditiile de necesitate si suficienta, reiese ca punctul x* este minimul functiei f daca:
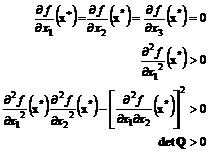 (3.40)
(3.40)
Se observa ca evaluarea minimului a fost realizata prin apelarea la metoda micilor perturbatii in punctul x pentru functia f, demonstrata prin utilizarea derivatelor partiale ale functiei f.
Se urmareste determinarea minimului unei functii supusa la anumite legaturi.
I. Formularea problemei:
Se considera o functie reala f=f(x,y) definita pe A2, in care variabila y este definita printr-o functie reala h ce depinde de variabila x:
![]() (3.41)
(3.41)
Plecand de la definitia unei curbe
se poate defini multimea ![]() , adica S(g) este multimea punctelor (x,y)
din A2 pentru care
functia g se anuleaza. Daca S(g) este o multime a punctelor x
din A2, atunci S(g) se va numi hipersuprafata din An determinata de g.
, adica S(g) este multimea punctelor (x,y)
din A2 pentru care
functia g se anuleaza. Daca S(g) este o multime a punctelor x
din A2, atunci S(g) se va numi hipersuprafata din An determinata de g.
Astfel, se defineste curba:
![]() (3.42)
(3.42)
Problema consta in determinarea minimului local (x*,y*) al functiei f de-a lungul curbei (3.41).
II. Determinarea conditiilor necesare de minim
Tinand cont de cele prezentate anterior, problema consta in determinarea punctelor (x*,y*) de pe curba (adica y*=h(x*)), astfel incat pentru un punct (x,y) de pe curba, suficient de apropiat de (x*,y*) are loc inegalitatea:
![]() . (3.43)
. (3.43)
Inlocuind
![]() (3.44)
(3.44)
in (3.43), se obtine:
![]() . (3.45)
. (3.45)
Punctul (x*,y*) se va numi minimul local al functiei f(x,y) cu legatura y-h(x)=0.
Gradientului functiei f in punctul de minim (x*,y*):
![]() . (3.59)
. (3.59)
Conditia de necesitate ca punctul (x*,y*) sa fie minimul functiei f cu legatura y-h(x)=0 reprezinta chiar conditia de anulare a gradientului functiei f in punctul de minim (x*,y*):
![]() (3.60)
(3.60)
adica:
![]() . (3.61)
. (3.61)
Concluzie:
S-a plecat de la ipoteza ca (x*,y*) este un punct de minim pentru functia f si s-a ajuns la conditia de necesitate (3.60).
III. Determinarea punctului de minim
Se ajunge la metoda multiplicatorilor Lagrange privind ecuatia
![]() din alt punct de vedere.
din alt punct de vedere.
Considerand functia
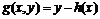 , (3.61)
, (3.61)
legatura poate fi scrisa sub forma:
![]() (3.62)
(3.62)
Pe baza relatiei (3.61) rezulta:
![]() (3.63)
(3.63)
Concluzie:
Derivata functiei g in raport cu y nu se anuleaza pe curba definita drept legatura.
Fie o functie diferentiabila
![]() (3.64)
(3.64)
atunci exista derivate partiale in fiecare punct (x,y) din A2
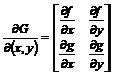 (3.65)
(3.65)
Jacobianul functiei G in punctul (x,y) este
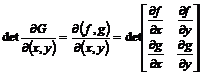 (3.66)
(3.66)
Stim ca 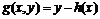 , din
(3.66) rezulta:
, din
(3.66) rezulta:
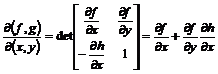 (3.67)
(3.67)
Astfel, ecuatia ![]() poate fi interpretata ca anularea Jacobianului
functiei G in punctul (x*,y*):
poate fi interpretata ca anularea Jacobianului
functiei G in punctul (x*,y*):
![]() (3.68)
(3.68)
Plecand de la relatia (3.68) se introduce sistemul:
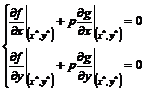 (3.69)
(3.69)
unde p se numeste multiplicator Lagrange.
Avand
in vedere ![]() , ecuatia a doua din (3.69) capata forma
, ecuatia a doua din (3.69) capata forma
![]() , (3.70)
, (3.70)
care permite determinarea multiplicatorului Lagrange in punctul de minim, p*, sub forma
![]() . (3.71)
. (3.71)
Inlocuind (3.71) in prima ecuatie a sistemului (3.69) rezulta:
![]() . (3.72)
. (3.72)
Dar, din 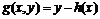
![]() , (3.73)
, (3.73)
relatia (3.72) devenind
![]() (3.74)
(3.74)
Relatia (3.74) este identica cu ![]() reprezentand conditia
de necesitate pentru minim.
reprezentand conditia
de necesitate pentru minim.
Se introduce functia:
![]() , (3.75)
, (3.75)
unde p este multiplicatorul Lagrange.
Pentru ca p in punctul (x*,y*) sa fie un punct de minim pentru functia G(x,y) trebuie ca derivatele partiale ale functiei G in raport cu (x,y) sa se anuleze in punctul (x*,y*):
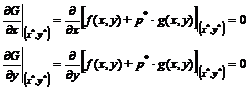 (3.76)
(3.76)
Concluzie:
Pentru ca punctul (x*,y*)
sa fie un punct de minim pentru functia f
cu legatura ![]() , este
necesara existenta unui numar p* astfel incat sa fie satisfacute urmatoarele
ecuatii:
, este
necesara existenta unui numar p* astfel incat sa fie satisfacute urmatoarele
ecuatii:
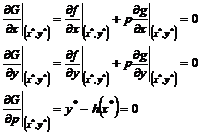 (3.77)
(3.77)
Exemplul 2:
Se da functia f definita pe A2 de forma:
![]() , (3.78)
, (3.78)
cu legatura
![]() .(3.79)
.(3.79)
Problema consta in determinarea minimului local (x*,y*) al functiei f de-a lungul curbei (3.79).
Rezolvare
Se formeaza functia:
![]() . (3.80)
. (3.80)
Pe baza conditiilor (3.77) se formeaza urmatorul sistem:
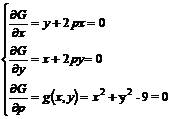 . (3.81)
. (3.81)
Din prima ecuatie a sistemului (3.81) rezulta multiplicatorul Lagrange:
![]() (3.82)
(3.82)
Inlocuind multiplicatorul p in ecuatia a doua din sistemul (3.81), rezulta:
![]() (3.83)
(3.83)
utilizand identitatea (3.83) in ecuatia curbei (3.79) se obtin solutiile:
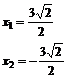 ,(3.84a)
,(3.84a)
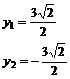 .
(3.84b)
.
(3.84b)
Solutiile (3.84ab) obtinute, inlocuite in (3.82) duc la urmatoarele valori ale multiplicatorului Lagrange
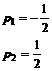 (3.85)
(3.85)
Calculul functiei in cele doua puncte conduce la aceeasi valoare a functiei in cele doua puncte de minim local determinate
![]() , (3.86)
, (3.86)
rezultand ca punctele de minim absolut sunt perechile
![]() (3.87)
(3.87)
![]() . (3.88)
. (3.88)
Se urmaresc urmatoarele:
1) formularea problemei de minim pentru functii multivariabile cu legaturi,
2) determinarea conditiilor necesare de minim,
3) rezolvarea problemei, adica determinarea punctului de minim.
Ipoteze: se da un domeniu D din An, o functie f definita pe An cu valori in A, f
(x)=f(x1,x2,,xn) continua pe domeniul inchis ![]() a lui D si functiile continue pe
a lui D si functiile continue pe ![]() , liniar
independente g1(x)=g1(x1,x2,,xn),
g2(x)=g2(x1,x2,,xn),, gm(x)=gm(x1,x2,,xn),
cu
, liniar
independente g1(x)=g1(x1,x2,,xn),
g2(x)=g2(x1,x2,,xn),, gm(x)=gm(x1,x2,,xn),
cu ![]() .
.
Se pune problema determinarii unui punct de minim
x*(x*1, x*2,, x*n) din domeniul
![]() , al functiei
f cu legaturile
, al functiei
f cu legaturile
g1(x)=0, g2(x)=0,, gm(x)=0(3.89)
Un punct x*(x*1, x*2,, x*n) din domeniul
![]() este un punct de minim local al functiei f cu legaturile (3.89), daca pentru un
numar e>0 suficient de mic exista un punct x
din
este un punct de minim local al functiei f cu legaturile (3.89), daca pentru un
numar e>0 suficient de mic exista un punct x
din ![]() situat in vecinatatea lui x*:
situat in vecinatatea lui x*:
![]() ,(3.90)
,(3.90)
astfel incat
![]() , (3.91)
, (3.91)
si
![]()
![]() (3.92)
(3.92)
In vederea determinarii punctului de minim se utilizeaza metoda multiplicatorilor Lagrange, prin care problema determinarii minimului x al functiei f cu legaturile (3.89) se inlocuieste cu problema determinarii minimului (x*,p*) al functiei:
![]() (3.93)
(3.93)
in care p=(p1,p2,,pm).
Conditiile necesare pentru determinarea minimului (x*,p*) sunt:
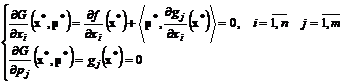 , (3.94)
, (3.94)
sau sub forma desfasurata:
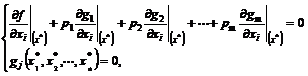 (3.95)
(3.95)
Se obtine astfel un sistem de ordinul n+m, cu n+m necunoscute x*(x*1, x*2,, x*n) si p*(p*1, p*2,, p*m), perechea (x*,p*) constituind punctul de minim local al functiei G(x,p) .
In vederea determinarii minimului absolut, se determina mai intai toate punctele de minim local. Acestea se mai pot afla pe frontiera domeniului de definitie si in punctele pentru care derivatele partiale ale functiilor f si g1, g2,, gn nu exista.
|
Politica de confidentialitate |
| |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |