Identitati trigonometrice.
Egalitatea
![]() unde U si V sunt expresii
care se obtin din expresiile analitice oarecare,
unde U si V sunt expresii
care se obtin din expresiile analitice oarecare, ![]()
![]() , prin substitutia
, prin substitutia ![]() se numeste identitate
trigonometrica (in raport cu variabila x) daca ea se verifica
pentru toate valorile admisibile ale lui x, pentru care membrul intai si
membrul al doilea se consider concomitant. Cele trei identitati
fundamentale, care leaga primele patru functii trigonometrice, sunt :
se numeste identitate
trigonometrica (in raport cu variabila x) daca ea se verifica
pentru toate valorile admisibile ale lui x, pentru care membrul intai si
membrul al doilea se consider concomitant. Cele trei identitati
fundamentale, care leaga primele patru functii trigonometrice, sunt :
![]()
![]()
Din acestea se pot deduce multe altele, dintre care mai frecvente sunt :
![]()
![]() si
si ![]()
Functiile trigonometrice exprimate cu ajutorul sinusului:
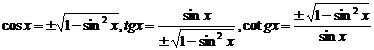
cu ajutorul cosinusului:
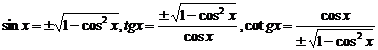
cu ajutorul tangentei:
![]()
cu ajutorul contangentei:
![]() .
.
Identitatile conditionate sunt identitatile in care arcele ce intervin sunt supuse anumitor conditii.
Exemple.
10. Daca ![]() , atunci
, atunci
![]() .
.
20.
Daca ![]() atunci
atunci
![]()
30. Daca ![]() , atunci
, atunci
![]() si o relatie analoga
pentru sinusuri.
si o relatie analoga
pentru sinusuri.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |