Metoda Newton se foloseste la rezolvarea numerica a ecuatiilor algebrice si transcendente, in cazul cind nu putem obtine solutiile ecuatiei f(x)=0 in forma analitica.
Se considera ecuatia f(x 0.
Functia f a,b]IR (functia definita pe [a, b]) , continua, f (x) 0 in acest interval si f (x) isi pastreaza semnul pe acest interval. Presupunem ca in urma unui proces de separare a radacinilor ecuatia f(x)=0 are o singura radacina x pe [a, b].
Algoritmul:
Pasul 1. Verificam daca la capetele intervalului functia ia valori de semn opus.
Pasul 2. Alegem o aproximatie initiala pe intervalul [a, b].
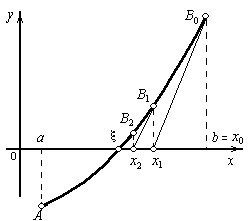
Notam prin x0, capatul intervalului, unde f²(x) > 0.
Pasul 3. Calculam x 1 punctul de intersectie al tangentei duse la graficul functiei in punctul
(x0, f(x0)) cu axa Ox.
Pentru a determina acest punct, vom scrie ecuatia dreptei tangenta la grafic in punctul de coordonate ( x0, f(x0)), si anume: y-f(x0)=f'(x0)(x -x0).
Daca in ecuatia de mai sus punem y=0, obtinem un numar x1 reprezentind abscisa punctului de intersectie al dreptei cu axa Ox:
f(x0)=-f'(x0)(x1-x0)
de unde rezulta: 
x1= -(f(x0)/f'(x0))+x0
Pasul 4. Daca f(x1 0, atunci este radacina cautata, altfel se duce tangenta in punctul (x1, f(x1)).
Pasul 5. Daca b/2/a| x0-x1|2 < e atunci oprim executia algoritmului, iar in calitate de solutie se va lua valoarea x1. In caz contrar iteram procesul pentru urmatoarea aproximare.
In cazul metodei Newton nu este necesar ca sa fie dat intervalul [а, b], care sa contina radacina ecuatiei f(x)=0, dar este suficient sa se determine prima aproximare a radacinii x = х0.
Utilizind metoda Newton este important sa tinem cont de urmatoarea regula: In calitate de prima aproximare х0 se alege acel capat al intervalului [а, b] cu solutia separata (daca acesta se cunoaste), sau alt careva punct din apropiere, pentru care f(x) are acelasi semn ca si derivata de ordinul doi f'' (х).
Numarul maxim de diviziuni al intervalului [а, b] poate fi obtinut apriori din relatia
, de unde cea mai mica valoare a lui n fiind:
|
Politica de confidentialitate |
 .com |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
