
Operatori pe clase de algebre. Varietati.
Prin operator vom intelege orice aplicatie definita pe o clasa de algebre de un anumit tip cu valori intr-o clasa de algebre de acelasi tip .
Prin K vom nota generic o clasa de algebre de un anumit tip.
In cele ce urmeaza vom pune in evidenta operatorii I, H, S, P, Ps, astfel:
Definitia 5.1.
. AII(K) daca si numai daca A este izomorfa cu o algebra de acelasi tip din K.
. AIS(K) daca si numai daca A este izomorfa cu o subalgebra a unei anumite algebre din K.
. AIH(K) daca si numai daca A este izomorfa cu imaginea printr-un morfism a unei algebre din K.
. AIP(K) daca si numai daca A este izomorfa cu un produs direct al unei familii nevide de algebre din K.
. A I Ps(K) daca si numai daca A este izomorfa cu un subprodus direct al unei familii nevide de algebre din K.
Daca O1, O2 sunt doi operatori, prin O1O2 vom nota compunerea lor (care este tot un operator).
Vom scrie O1 O2 daca si numai daca O1(K) O2(K) pentru orice clasa K de algebre.
Operatorul O se va zice idempotent daca O2 = O.
O clasa de algebre K se va zice inchisa fata de un operator O daca O (K) K
Daca notam prin O unul dintre operatorii I, S, H, P, PS definiti mai inainte, observam ca O restrictionat la clasa algebrelor de un anumit tip verifica conditiile: K O (K), K1 K2 T O (K1) O (K2) si O (O(K)) = K pentru orice clase de algebre de acelasi tip K, K1, K2, de unde concluzia ca O poate fi privit ca operator de inchidere pe clasa tuturor algebrelor de un anumit tip.
De asemenea, daca A I K observam ca orice algebra izomorfa cu A apartine lui K. Simbolic vom scrie ca O = I O; avem de asemenea si egalitatea O I = O.
Lema 5.2. Operatorii HS, SP, HP si HPS sunt operatori de inchidere pe clase algebrice de un anumit tip.
De asemenea: SH HS, PS SP, PH HP, PSH HPS si PSP = PS = PPS iar PSS = SP = SPS.
Demonstratie: Este usor de vazut ca daca compunem doi operatori ce verifica conditiile K O (K) si K1 K2 T O (K1) O (K2) obtinem un operator cu aceleasi priprietati. Mai mult (restrictionand aceasta clasa de operatori) compunerea este o operatie asociativa si pastreaza ordinea
Astfel, operatorii HS, SP, HP si HPS verifica imediat axiomele operatorilor de inchidere.
Pentru conditia de idempotenta putem folosi celelalte relatii (de exemplu daca acceptam ca SH HS, atunci (HS)2 = (HS)(HS) = H(SH)S H(HS)S = HHSS = HS iar pe de alta parte HS = (HI) (IS) (HS) (HS) = (HS)2) asa ca este suficient ca sa probam una din inegalitatile de forma SH HS (celelalte probandu-se analog).
Sa probam de exemplu
ca PH HP. Pentru aceasta
fie K o clasa de algebre de
acelasi tip si A I K.
Atunci ![]() cu Ai I H(K)
pentru orice i I I. Putem alege Bi I K si morfismele surjective
fi : Bi Ai pentru orice iII. Atunci avem morfismul surjectiv g:
cu Ai I H(K)
pentru orice i I I. Putem alege Bi I K si morfismele surjective
fi : Bi Ai pentru orice iII. Atunci avem morfismul surjectiv g:![]()
![]() definit prin g((bi)iII) = (fi(bi))iII. Cum fg :
definit prin g((bi)iII) = (fi(bi))iII. Cum fg : ![]() A este un morfism surjectiv, deducem
ca A I HP(K).g
A este un morfism surjectiv, deducem
ca A I HP(K).g
Definitia 5.3. Vom spune ca o clasa de algebre K de un anumit tip este varietate daca ea este inchisa relativ la operatorii H, S si P (adica H (K) K, S (K) K si P (K) K).
Prin V (K) vom nota cea mai mica varietate (fata de incluziune) ce contine pe K si o vom numi varietatea generata de K (daca K contine o singura algebra A sau un numar finit A1, , An atunci vom scrie V (A) sau V (A1, , An) pentru V(K)). Obtinem in felul acesta un nou operator V.
Teorema 5.4. (Tarski). V= HSP.
Demonstratie: HHSP =
SHSP = PHSP = HSP, de unde rezulta ca HSP (K) este o varietate ce contine pe K pentru orice clasa K.
Pe de alta parte, daca ![]() este o
varietate ce contine pe K,
atunci HSP ( K ) HSP (
este o
varietate ce contine pe K,
atunci HSP ( K ) HSP (![]()
![]() , adica
HSP (K) este cea mai mica
varietate ce contine pe K, de
unde HSP = V.g
, adica
HSP (K) este cea mai mica
varietate ce contine pe K, de
unde HSP = V.g
Propozitia 5.5. Fie K o clasa de algebre de un anumit tip iar A o algebra de acelasi tip.
i) A I SP (K) exista o familie de congruente (qi)iII pe A astfel incat ![]() qi DA si A qi I S (K) pentru orice i I I.
qi DA si A qi I S (K) pentru orice i I I.
ii) A IHSP
(K) exista o algebra B,
congruentele (qi)i II si q pe B astfel incat B q A q ![]() qi si B qi I S (K) pentru orice i I I. g
qi si B qi I S (K) pentru orice i I I. g
Observatie: Operatorii I, H, S si P genereaza un monoid ordonat a carui structura a fost determinata in 1972 de Pigozzi si are urmatoarea diagrama Hasse:
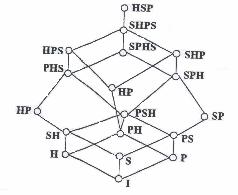
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |