
Functii reale de mai multe variabile reale
§.1.Functii reale de mai multe variabile reale
Structura topologica a spatiului Rn
Fie X . Se numeste distanta (metrica) pe X, o functie d:X X R, cu proprietatile:
x,yIX d(x,y) 0 si d(x,y)=0 x=y ;
x,yIX d(x,y) = d(y,x) ;
x,y,zIX d(x,z)![]() d(x,y) + d(y,z).
d(x,y) + d(y,z).
Perechea (X,d), cu X si d metrica pe X se numeste spatiu metric.
Pe aceeasi multimea X se pot defini diverse metrice, deci mai multe structuri de spatiu metric.
Fie (X,d) un spatiu metric, x0IX si numarul real, oarecare, r>0. Multimea
Br(x0)=
se numeste bila deschisa cu centrul x0 si raza r.
Se numeste bila inchisa cu centrul in x0 si raza r, multimea notata Br[x0] si definita prin:
Br[x0] = .
In Rn distanta
dintre doua puncte x=(x1,x2,.,xn) si y=(y1,y2,..,yn)
se poate defini
ca fiind numarul real d(x,y) = 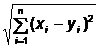 . Aceasta se numeste distanta euclidiana dintre cele
doua puncte. Se poate verifica usor ca d este o metrica pe Rn.
Pentru n=1 distanta euclidiana este d(x,y)=
. Aceasta se numeste distanta euclidiana dintre cele
doua puncte. Se poate verifica usor ca d este o metrica pe Rn.
Pentru n=1 distanta euclidiana este d(x,y)=![]() , iar pentru n=2, d(x,y)=
, iar pentru n=2, d(x,y)= ![]()
Fie (X,d) spatiu metric si x0IX.Se numeste vecinatate a lui x0, orice submultime V X, pentru care exista r >0, astfel incat Br(x0) V.
Definitia 1.6. O submultime D X se numeste deschisa daca x0ID, r > 0 astfel incat Br(x0) D ( D este vecinatate pentru fiecare punct al sau).
Pentru Rn, cu n=1, o bila deschisa cu centrul in x0IR este un interval deschis simetric fata de x0, de forma (x0-r, x0+r) ; o bila inchisa este intervalul inchis [x0-r, x0+r].
Pentru n=2, bila deschisa este un disc circular cu centrul in x0 si raza r, iar bila inchisa contine si circumferinta impreuna cu discul.
Pentru n=3, bila deschisa cu centrul in x0IR si raza r este interiorul sferei cu centrul in x0 si raza r, bila inchisa este formata din sfera si interiorul ei.
Fie (X,d) spatiu metric si A X. Un punct xIA se numeste punct interior multimii A, daca r >0 astfel incat Br(x) A.
Toate
punctele interioare multimii A formeaza interiorul lui A , care se noteaza ![]() .
.
Fie (X,d) spatiu metric si A X. Un punct xIX se numeste punct aderent multimii A, daca r > Br(x) A
Toate punctele aderente multimii A formeaza inchiderea
lui A, notata ![]() .
.
Multimea notata ![]()
![]() se numeste frontiera
( bordul) lui A.
se numeste frontiera
( bordul) lui A.
Un punct xIX, aderent multimii A, cu proprietatea
r > Br(x) A
se numeste punct de acumulare al lui A.
Multimea punctelor de acumulare pentru A se noteaza A' si se numeste multimea derivata a lui A.
O submultime A a spatiului metric (X,d) se numeste marginita daca r >0 si x0IX, astfel incat A Br(x0).
O clasa importanta de spatii metrice sunt spatiile vectoriale normate.
Fie X/K spatiu vectorial.
Functia ![]() :X R, cu proprietatile:
:X R, cu proprietatile:
![]() , xIX
si
, xIX
si ![]() x qV
x qV
![]() lIK, xIX
;
lIK, xIX
;
![]() , x,yIX.
, x,yIX.
se numeste norma pe X.
Un spatiu vectorial X impreuna cu o norma definita pe X se numeste spatiu normat.
Un
spatiu vectorial normat este un spatiu metric cu distanta
indusa de norma sa astfel: d(x,y)= ![]() , x,yIX.
, x,yIX.
Daca X= Rn, n 1, ![]() , x=(x1,x2,.,xn)IRn ; iar pentru n=1,
, x=(x1,x2,.,xn)IRn ; iar pentru n=1, ![]() , xIR; astfel Rn este
un spatiu
vectorial normat.
, xIR; astfel Rn este
un spatiu
vectorial normat.
O functie f:A Rn R, care asociaza fiecarui vector x=(x1,x2,.,xn)IRn numarul real f(x1,x2,.,xn) se numeste functie reala de n variabile reale.
Exemple.
1.f:Rn R , f(x1,x2,.,xn)=a1x1+a2x2+.+anxn, cu a1,a2,.., anIR se numeste functie liniara de n variabile reale sau functionala liniara.
2.f:A R2 R , f(x,y)=![]() este o functie reala de doua variabile reale.
Multimea maxima de definitie este A= R2
.
este o functie reala de doua variabile reale.
Multimea maxima de definitie este A= R2
.
3.Functia Cobb-Douglas f:D R2 R,f(x,y)=Axby1-b definita pe D= cu constantele A>0, bI(0,1).Ea reprezinta legatura dintre doi factori de productie x si y si volumul eficientei productiei f(x,y) pentru diferite valori ale acestor factori. De obicei, x reprezinta suma de bani cheltuita pentru forta de munca, iar y este suma de bani cheltuita pentru mijloace fixe cladiri, utilaje si mijloace de productie). Functia f masoara produsul final si de aceea se numeste functie de productie.
Limite si continuitate pentru functiile reale
Fie functia reala de n variabile reale f:A Rn R si fie a un punct de acumulare pentru A.
Numarul lIR
se numeste limita functiei f in punctul aIRn si se noteaza l=![]() , daca pentru orice vecinatate U a lui l exista o vecinatate
V a punctului a astfel incat xIV
A , f(x)IU.
, daca pentru orice vecinatate U a lui l exista o vecinatate
V a punctului a astfel incat xIV
A , f(x)IU.
Fie functia f:A Rn R, aIA un punct de acumulare pentru A si lIR. Urmatoarele afirmatii sunt echivalente:
Numarul l este limita functiei f in punctul a
Pentru e> d>0, astfel incat xIA,
x a cu proprietatea ![]() <d T f(x) - l < e
<d T f(x) - l < e
Pentru orice sir (xn)nIN de
puncte din A, xn a cu ![]() T
T ![]() .
.
Consecinta. Daca exista doua siruri (xn) si (xn') cu aceeasi limita a, astfel incat sirurile de valori ale functiei f, (f(xn))n si (f(xn'))n au limite distincte sau cel putin unul dintre aceste siruri nu este convergent, atunci functia f nu are limita in punctul a.
Exemple.1. Fie functia f :R2 R prin f(x,y) =3x-2y. Punctul a=(-1,2)
este punct de acumulare pentru R2. Vom considera un sir xn= (xn1,
xn2) R2 convergent
catre a. El este format din sirurile de numere (xn1)
si (xn2) 2.
Calculam
limita sirului ![]() =
= ![]() = -7, folosind operatiile cu siruri de numere reale.
= -7, folosind operatiile cu siruri de numere reale. ![]() .
.
Continuitatea functiilor reale
Fie functia f:A Rn R, si fie a IA. Functia f se numeste continua in punctul a IA, daca pentru orice vecinatate U a punctului f(a), exista o vecinatate a punctului aIA, astfel incat pentru orice x IV A , f(x)IU.
Functia f:A Rn R se numeste continua pe multimea A daca este continua in orice punct al multimii A.
Un punct xIA, in care functia f nu este continua se numeste punct de discontinuitate al functiei f.
Fie functia f:A Rn R si a IA.Urmatoarele afirmatii sunt echivalente
1. Functia f este continua in a IA
2. Pentru e> d>0, astfel incat xIA,
x a cu proprietatea ![]() <d T f(x) - f(a) < e
<d T f(x) - f(a) < e
3.Pentru orice sir (xn)nIN de
puncte din A, xn a cu ![]() , sirul de valori (f(xn))n este convergent si are
, sirul de valori (f(xn))n este convergent si are ![]() .
.
Daca aIA,
este in plus si punct de acumulare pentru A, atunci definitia
continuitatii coincide cu definitia limitei si deci f este
continua in a ![]() .
.
Reamintim, pentru inceput, cateva notiuni legate de derivabilitatea functiilor reale de o variabila reala, cunoscute din liceu.
Fie functia f:D R R
si x0ID D'. Spunem ca functia f are
derivata in punctul x0 ,
daca exista in ![]() ,
, ![]() (sau notata
(sau notata ![]() ).
).
Aceasta limita se numeste derivata functiei f in x0. Daca derivata f '(x0) este finita, atunci spunem ca functia f este derivabila in punctul x0. Functia f:D R R se numeste derivabila pe A D, daca este derivabila in orice punct xIA.
Daca functia f este devabila pe A D, se poate defini functia f :A R, x f (x), numita derivata functiei f.
Fie I,J R, intervale de numere reale, f:I J, g:J R. Daca f este derivabila in x0 si g este derivabila in y0=f(x0)IJ,atunci g f:I R este derivabila in x0 si
(g![]() f)(x0)=g (f(x0)) f (x0).
f)(x0)=g (f(x0)) f (x0).
Fie f:D R R. Un punct x0ID se numeste punct de minim (respectiv de maxim) local pentru f, daca exista o vecinatate a lui x0, VIV(x0), astfel incat f(x) f(x0) (respectiv f(x) f(x0)) xID V.
Un punct x0ID se numeste punct de extrem local, daca este punct de minim local sau maxim local.
Teorema lui Fermat
Fie
f:I R R, I interval. Daca x0I![]() este punct de extrem local pentru f si f este derivabila in x0
atunci f (x0)=0.
este punct de extrem local pentru f si f este derivabila in x0
atunci f (x0)=0.
Fie f:I R R,
I interval. Un punct x0I![]() , in care f este derivabila si f (x0)=0
se numeste punct critic (sau stationar) pentru f.
, in care f este derivabila si f (x0)=0
se numeste punct critic (sau stationar) pentru f.
Reciproca teoremei lui Fermat nu este in general adevarata.
Fie f:I R R, I interval, f continua pe I, x0II
astfel incat f este derivabila pe I si ![]() si este finita. Atunci f este derivabila in x0
si
si este finita. Atunci f este derivabila in x0
si
f (x0) =![]() .
.
Derivate de ordin superior ale functiilor reale de o variabila reala
Fie functia f:I R R , I este un interval deschis, f derivabila pe I si x0II.
Daca f este functie derivabila intr-o vecinatate VIV(x0) si functia derivata f este derivabila in x0, atunci derivata functiei f in punctul x0 se numeste derivata de ordinul doi a functiei f in x0 si se noteaza:
f "(x0) = ![]() (x0) (1)
(x0) (1)
Recursiv, se obtine derivata de ordinul n 2 : daca exista functia derivata de ordinul n-1 a functiei f intr-o vecinatate VIV(x0), notata f(n-1), si este derivabila in x0, atunci derivata sa in x0 se numeste derivata de ordin n a functiei f in punctul x0 si se noteaza
f (n)(x0)
= [f (n -1)] '(x0) = 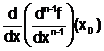 =
= ![]() (x0) (2)
(x0) (2)
Fie f,g :I R R, doua functii reale. Daca f si g sunt functii derivabile de ordinul n I N* in x0 II si a bIR, atunci:
i) functia af + bg:I R R este derivabila de ordinul n in x0 si are loc egalitatea:
(af + bg)(n)(x0) = af (n)(x0) + bg (n)(x0) (3)
ii) functia f g:I R R este derivabila de ordinul n in x0 si
(f g)(n)(x0)=![]() (4)
(4)
Daca f :I R R este derivabila pana la ordinul n+1 pe I, iar aII este un punct pentru care:
f '(a) = f '(a) =.= f (n-1)(a) = 0 si f (n)(a) (5)
i)daca n este par T a este punct de extrem local pentru f si anume:
a)daca f (n)(a) > 0 T a este punct de minim local pentru f;
b)daca f (n)(a) < 0 T a este punct de maxim local pentru f;
ii)daca n este impar atunci a nu este punct de extrem local pentru f.
Fie f : D Rk R, k
2, x0 = (![]() ,
, ![]() , .,
, ., ![]() )I D un punct fixat in D si x = (x1, x2, .,
xk)ID un punct curent. Pentru k 2, notiunea de derivata nu
mai poate fi introdusa ca in cazul k = 1.
)I D un punct fixat in D si x = (x1, x2, .,
xk)ID un punct curent. Pentru k 2, notiunea de derivata nu
mai poate fi introdusa ca in cazul k = 1.
Derivatele functiilor reale de mai multe variabile reale (derivatele partiale) se introduc cu ajutorul derivatei dupa directia unui versor.
Fie s = (s1, s2, ., sk) I Rk cu ||s|| = 1. Construim o functie g : R R
g(t) = f(x0 + ts) = f(x10 + ts1, x20 + ts2, ., xk0 + tsk), t I R, astfel incat x0 + ts I D si s I Rk. (6)
Deoarece, D Rk si x0 I Rk rezulta ca r > 0 astfel incat Br(x0) D si pentru acest r > 0 T functia g din (6) este bine definita pe intervalul (- r, r)
g: (- r, r) R, g(t) = f(x0+ts), ( ) t I (- r, r).
Functia f :D Rk R se numeste derivabila in x0ID, dupa directia versorului sIRk daca functia g : (- r, r) R, g(t) = f(x0 + ts), t I (- r, r)
este derivabila in t = 0, iar numarul
g '(0)
= ![]() =
= ![]() (7)
(7)
se numeste derivata functiei f in punctul x0 dupa directia versorului s.
Daca notam x = x0 + tsID, t I (- r, r), x0 I D, s I Rk vectorul curent, atunci t x x0 si (10) devine:
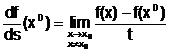 , x - x0 =
ts. (8)
, x - x0 =
ts. (8)
Fie D Rk,
x0ID. Functia f :D Rk R se numeste derivabila
partial in punctul x0 ID in raport cu variabila xi, i = ![]() , daca f este derivabila in punctul x0 I D dupa directia versorului
unitar ei =
, daca f este derivabila in punctul x0 I D dupa directia versorului
unitar ei = ![]() I Rk .
I Rk .
In acest caz, numarul notat:
![]() (x0) =
(x0) = ![]() (x0) =
(x0) =![]() (x0), i =
(x0), i = ![]()
se numeste derivata
partiala a functiei f in punctul x0, in raport xi,
i = ![]() .
.
Rezulta: ![]() (x0) =
(x0) =![]() (x0) =
(x0) =![]()
![]()
si daca notam xi = xi0
+ t, i = ![]() , daca t T xi
xi0, i =
, daca t T xi
xi0, i = ![]() si deci:
si deci:
![]() (x0) =
(x0) = ![]() =
=![]() (x0), i =
(x0), i = ![]() (9)
(9)
Functia
f : D Rk R
derivabila partial in raport cu variabila xi in fiecare
punct din multimea D se numeste derivabila partial in raport cu
variabila xi, i = ![]() pe multimea D.
pe multimea D.
Functia f se numeste derivabila partial in x0ID, daca este derivabila partial in raport cu toate variabilele sale in punctul x0.
Daca pentru fiecare i =![]() , consideram functiile partiale fi
: xi a f(x1, ., xk),
in care sunt fixate componentele x1, ., xi-1, xi+1,.,
xk ale vectorului x=(x1,.,xi,., xk)ID, atunci definitia derivatei
partiale a functiei f in raport cu componenta xi, i =
, consideram functiile partiale fi
: xi a f(x1, ., xk),
in care sunt fixate componentele x1, ., xi-1, xi+1,.,
xk ale vectorului x=(x1,.,xi,., xk)ID, atunci definitia derivatei
partiale a functiei f in raport cu componenta xi, i =![]() , este aceeasi cu definitia derivatei functiei
partiale fi, functie reala de variabila
reala xi .
, este aceeasi cu definitia derivatei functiei
partiale fi, functie reala de variabila
reala xi .
Pe baza aceste observatii, regulile de derivare de la functii de variabila reala se aplica si pentru derivatele partiale ale functiilor de mai multe variabile reale, cu mentiunea ca, pentru acestea din urma, atunci cand se calculeaza derivata partiala in raport cu variabila xi aceste reguli se aplica pentru aceasta variabila xi si se considera constante celelalte k-1 variabile.
Functia f : D Rk R, k 2, se numeste derivabila partial (de ordinul I) pe multimea D daca este derivabila partial in fiecare punct din D (in raport cu toate componentele vectorului x = (x1, ., xk) I D).
Aceasta inseamna ca
( )x = (x1, ., xk) I D si ( i = ![]() , exista derivatele partiale de ordinul intai
, exista derivatele partiale de ordinul intai ![]() (x), i =
(x), i = ![]() .
.
Se pot construi k functii, notate ![]() : D R, i =
: D R, i = ![]() , prin x a
, prin x a ![]() (x), x I D, numite functiile
derivate partiale de ordinul I ale functiei f .
(x), x I D, numite functiile
derivate partiale de ordinul I ale functiei f .
Daca
D Rk, k 2, atunci f:D R se numeste de
clasa C1 pe multimea D (se noteaza fIC1(D)), daca f este
derivabila partial pe multimea D si toate functiile derivate
partiale (de ordinul I), ![]() ,.,
,., ![]() :D R, sunt functii continue pe D.
:D R, sunt functii continue pe D.
Exemplu. Sa se calculeze derivatele partiale de ordinul I ale functiei
f(x,y)=![]() .
.
Derivatele partiale de ordinul I sunt:
![]() ;
; ![]() =
=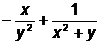 .
.
Functia f : D Rk R se numeste diferentiabila in x0ID
daca exista A=(A1,A2,.,Ak)IRk si o functie h:D R cu
proprietatea ca: ![]() , astfel incat:
, astfel incat:
f(x) - f(x0) = <A, x-x0> + ||x - x0|| h(x), x I D. (20)
Functia f se numeste diferentiabila pe multimea D daca este diferentiabila in fiecare punct din multimea D.
Daca f : D Rk R este diferentiablia in x0 I D Rk, atunci forma liniara
<A, x - x0> = A1 (x1 - x10) + A1 (x2 - x20) + . + Ak (xk - xk0) (21)
se numeste diferentiala functiei f in x0 si se noteaza:
df(x0) = <A, x - x0> = A1 (x1 - x10) + A1 (x2 - x20) + . + Ak (xk - xk0). (22)
Se poate demonstra ca diferentiala unei functii intr-un punct x0ID este unica si depinde numai de punct si de functie.
Daca f : D Rk R este diferentiabila in x0 I D, atunci:
I) f este continua in x0;
II) f este derivabila partial in x0 .
Daca f :D Rk R este diferentiabila pe multimea D, atunci f este derivabila partial pe multimea D.
Fie f :D Rk R, x0ID.
Daca f este derivabila partial pe o vecinatate VIV(x0),
V
D si toate functiile derivate partiale (de ordinul I) ![]() ,.
,.![]() sunt continue in x0 ID, atunci f este
diferentiabila in x0 ID.
sunt continue in x0 ID, atunci f este
diferentiabila in x0 ID.
Orice functie elementara este diferentiabila pe orice deschis din multimea ei de definitie.
Diferentiala functiei f este forma liniara
df(x0)(h) = (![]() h1+
h1+ ![]() h2 + . +
h2 + . + ![]() hk, h=( h1,
h2,.,hn)IRk
hk, h=( h1,
h2,.,hn)IRk
Orice aplicatie liniara L:Rk R este diferentiabila pe Rk si pentru x0IRk, dL(x0)=L.
In particular, proiectiile pri: Rk R, (x1,x2,..,xk) xi ,1 i n, sunt diferentiabile si
d pri (x0)= pri, x0IRk
Vom nota diferentialele acestor proiectii cu dxi , 1 i n.
df(x0) = ![]() dx1 +
dx1 + ![]() dx2 + . +
dx2 + . + ![]() dxk. (23)
dxk. (23)
Daca interpretam, in mod formal, functia
derivata partiala, ![]() ,( i=
,( i=![]() ) ca un produs
intre
) ca un produs
intre ![]() si f, atunci
formula (23) a diferentialei functiei f in x0 se scrie:
si f, atunci
formula (23) a diferentialei functiei f in x0 se scrie:
df(x0) = (![]() dx1 +
dx1 + ![]() dx2 + . +
dx2 + . + ![]() dxk) f(x0). (24)
dxk) f(x0). (24)
Exemplu. Sa se stabileasca expresia diferentialei de ordinul I a functiei f definita prin f(x,y)=ln(x2+y2), (x,y) intr-un punct oarecare din domeniul de definitie si in punctul x0=(1,2).
![]() ;
; ![]() ;
;
df(x,y)= ![]() +
+![]() ; iar df(1,2)=
; iar df(1,2)=![]() +
+![]() .
.
Derivate partiale si diferentiale de ordin superior ale functiilor
Fie f :D Rk R, k
2. Presupunem ca f este derivabila partial pe multimea D
si exista ![]() : D R, functiile derivate
partiale de ordinul I ale functiei f in raport cu toate componenetele
xi, in fiecare x = (x1,
., xk)ID.
: D R, functiile derivate
partiale de ordinul I ale functiei f in raport cu toate componenetele
xi, in fiecare x = (x1,
., xk)ID.
Daca toate functiile derivate partiale de
ordinul I ale functiei f, ![]() , .,
, ., ![]() sunt functii
derivabile partial pe multimea D, atunci functiile derivate
partiale ale acestora se numesc derivatele partiale de ordinul doi
ale functiei f pe D si se noteaza:
sunt functii
derivabile partial pe multimea D, atunci functiile derivate
partiale ale acestora se numesc derivatele partiale de ordinul doi
ale functiei f pe D si se noteaza:
![]() =
=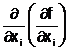 i =
i = ![]() , numite functiile derivate partiale de ordinul doi
in raport cu xi de doua ori;
, numite functiile derivate partiale de ordinul doi
in raport cu xi de doua ori;
![]() =
=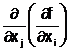 ;
;![]() =
=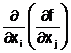 , i, j =
, i, j = ![]() , i j, numite derivatele
partiale de ordinul doi mixte ale functiei f in raport cu xi,
xj si respectiv xj, xi.
, i j, numite derivatele
partiale de ordinul doi mixte ale functiei f in raport cu xi,
xj si respectiv xj, xi.
Recursiv, se definesc derivatele partiale de ordinul n 2 ale functiei f, ca fiind derivatele partiale de ordinul I ale functiilor derivate partiale de ordinul n - 1.
Teorema lui Schwartz
Fie f :D Rn R o functie de clasa C2(D) ( fIC1(D) si toate derivatele partiale de ordinul intai sunt de clasa C1(D)). Atunci
![]()
![]() , aID,
, aID, ![]() .
.
Exemplu.Sa se calculeze derivatele partiale de ordinul al doilea ale functiei
f(x.y)=3x2y + 5![]() , (x,y)IR2, y si sa
se verifice teorema lui Scwartz.
, (x,y)IR2, y si sa
se verifice teorema lui Scwartz.
![]() ;
; ![]() .
.
Calculam derivatele de ordinul al doilea:
![]() =6y ;
=6y ; ![]() =6x -
=6x -![]() ;
;
![]() =
=![]() ;
; ![]() =6x -
=6x -![]() .
.
Fie f:D Rn R , derivabila partial de
doua ori in punctul x0ID. Matricea H(x0)=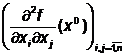 IMn(R) se
numeste matricea hessiana
a functiei f in punctul x0.
IMn(R) se
numeste matricea hessiana
a functiei f in punctul x0.
Exemplu.
Sa se scrie Hessiana functiei f:D R2 R,
f(x,y)=ln![]() in punctul x0=(2,1).
in punctul x0=(2,1).
Vom calcula derivatele partiale de ordinul I si II ale acestei functii.
![]() ;
; 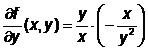 =
=![]() ;
;![]() ;
;![]() = -1
= -1
![]() =
=![]() ;
; ![]() = 0;
= 0;
![]() =
=![]() ;
;![]()
![]() ;
;![]() 0;
0; ![]() 1.
1.
Hessiana in x0 este H(x0)=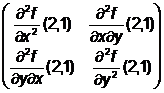 =
=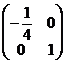 .
.
Functia f :D Rk R se numeste diferentiabila de ordinul n 2 in x0ID daca toate functiile derivate partiale de ordinul n-1 exista intr-o vecinatate VIV(x0) si acestea sunt diferentiabile in x0.
Daca f :D Rk R este diferentiabila de ordinul n in x0I D, atunci derivatele partiale de ordinul n in x0 exista si ordinea de derivare pana la ordinul n in x0 este indiferenta.
Daca f:D Rk R este derivabila partial de ordinul n intr-o vecinatate VIV(x0) si toate functiile derivate partiale de ordinul n sunt continue in x0, atunci f este diferentiabila de ordinul n in x0.
Diferentiala de ordinul n a functiei f :D R R se defineste recursiv prin egalitatea:
dnf(x0,
y0) = d(dn -1(f))(x0, y0) = 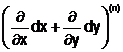 f(x0, y0) unde
f(x0, y0) unde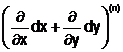 reprezinta puterea simbolica a n-a pentru
operatorul de diferentiere.
reprezinta puterea simbolica a n-a pentru
operatorul de diferentiere.
Exemplu. d2f(x0,y0)=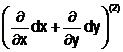 f(x0,y0)=
f(x0,y0)=
=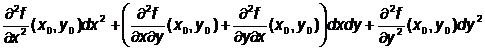 .
.
In general, daca f : D Rk R, k 2, este diferentiabila de ordinul n in x0ID, atunci diferentiala de ordinul n a functiei f in x0 se defineste prin :
dnf(x0)=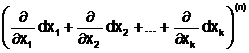 f(x0) =
f(x0) =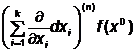 .
.
Formula lui Taylor pentru functii de doua variabile
Fie f:D R2 R si (a,b) un punct interior din D. Presupunem ca f este de n ori diferentiabila in punctul (a,b), deci exista toate derivatele de ordin n in (a,b) si sunt continue.
Polinomul :
Tn(x,y)=f(a,b)+![]() + +
+ +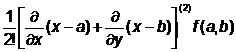 +
+
+..+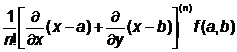
se numeste polinomul Taylor de gradul n atasat functiei f in (a,b).
Rn(x,y)= f(x,y)-Tn(x,y) se numeste restul de ordinul n al formulei lui Taylor.
Restul Rn(x) estimeaza eroarea aproximarii functiei f(x,y) prin polinomul lui Taylor de ordin n, Tn(x,y).
Daca functia f:D R2 R este diferentiabila de n+1 ori intr-o vecinatate a punctului interior (a,b)ID, atunci pentru orice punct (x,y) din aceasta vecinatate exista un punct x h) situat pe segmentul cu capetele (x,y) si (a,b), astfel incat
Rn(x,y)= 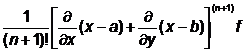 (x h
(x h
Formula lui Taylor de ordinul n corespunzatoare lui f se va scrie
f(x,y)=f(a,b)+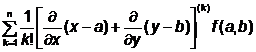 +
+
+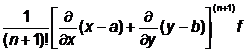 (x h
(x h
Fie f:D R2 R o functie care are derivate
partiale de ordinul al doilea intr-o vecinatate a punctului (a,b). Atunci exista o functie w(x,y) continua in (a,b) si ![]() astfel incat
astfel incat
R2(x,y)=![]() .
.
§.3.Extremele functiilor reale de mai multe variabile reale
Multe dintre problemele care apar in practica sunt legate de determinarea valorilor extreme ale unei functii reala ce depinde de mai multe variabile. De exemplu, o functie poate reprezenta volumul productiei, care depinde de mai multe variabile reale este bine sa cunoastem pentru ce valori ale variabilelor volumul productiei este maxim.Valorile maxime sau minime ale unei functii se numesc extremele functiei. Am definit mai sus, notiunea de punct de minim si respectiv maxim local.
Fie f:D R2 R si x0=(a,b)ID.
Teorema (Conditiile necesare pentru existenta unui extrem)
Daca functia f admite derivate partiale de ordinul intai intr-o vecinatate a punctului x0 si x0 este punct de extrem local pentru functia f, atunci derivatele partiale ale lui f sunt nule in acest punct, adica:
![]() ,
, ![]() .
.
Punctele determinate de solutiile reale ale sistemului
de ecuatii ![]() ,
, ![]() se numesc puncte
critice sau stationare.
se numesc puncte
critice sau stationare.
Teorema ( Conditia suficienta de extrem)
Functia f: D R2 R, care admite derivate partiale de ordinul al doilea pe D, are un punct de extrem local in punctul stationar (a,b)ID, daca:
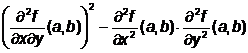 <
<
Punctul (a,b) este punct de maxim
local daca ![]() < 0 si este punct de minim
local al functiei f daca
< 0 si este punct de minim
local al functiei f daca ![]() >
>
Notam
cu a11=![]() , a12=
, a12=![]() si a22
si a22![]() si putem scrie Hessiana lui f in acest punct Hf(x0)
si putem scrie Hessiana lui f in acest punct Hf(x0)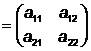 .
.
Rezulta ca punctul
stationar (a,b) este punct de minim local pentru f daca
determinantii D a11 > 0 si D2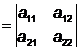 >0 si
>0 si
este punct de maxim local daca D < 0 si D >
Exemplu. Sa se determine punctele de extrem local ale functiei
f(x,y)=3x3+y2-9x2-27x+2.
Vom determina mai intai punctele stationare ale lui f, rezolvand sistemul de ecuatii
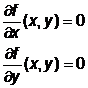
![]() .
.
Exista doua puncte stationare M1 si M2(3,0). Pentru a vedea care dintre ele este punct de extrem local pentru f, va trebui sa calculam derivatele de ordinul al doilea ale lui f.
![]() ;
; ![]() ;
; ![]() care sunt functii continue pe R2.
care sunt functii continue pe R2.
In punctul M1 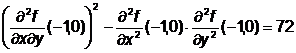 >0, deci nu este extrem.
>0, deci nu este extrem.
In punctul M2(3,0):
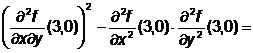 -72<0 si
-72<0 si ![]() =36>0, deci M2 este
punct de minim local al functiei f. Valoarea minima a functiei f
este f(3,0)= -79.
=36>0, deci M2 este
punct de minim local al functiei f. Valoarea minima a functiei f
este f(3,0)= -79.
Fie functia f:D Rn R de n variabile reale, n>
Un punct stationar pentru functia f este o solutie a sistemului de n ecuatii cu n necunoscute:
![]()
![]()
![]()
Vom considera a=(a1,a2,.,an)IA un punct stationar al lui f. Presupunem ca f admite derivate
partiale de ordinul doi continue intr-o vecinatate a acestui punct si le vom nota cu aij![]() , i,j
, i,j![]() .
.
Hessiana lui f in punctul a este matricea H=(aij)![]() , ale carei elemente sunt definite mai sus. Notam determinantii
principali ai matricei H cu
, ale carei elemente sunt definite mai sus. Notam determinantii
principali ai matricei H cu ![]() ;
;
D a11 si D2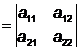 Dn=det H.
Dn=det H.
Daca D > D > Dn>0 atunci a este un punct de minim local pentru functia f
daca D < D > D <0..( semnele alterneaza incepand cu minus), atunci a este punct de maxim local. In celelalte cazuri punctele stationare nu sunt puncte de extrem.
Metoda aceasta de studiu a punctelor de extrem local ale unei functii reale de mai multe variabile reale consta in calculul diferentialei de ordinul al doilea a functiei in fiecare punct critic si daca este o forma patratica pozitiv definita atunci punctul critic studiat este minim local ; iar daca este negativ definita atunci este maxim local al functiei respective.
Probleme propuse
Fie functia f:D R2 R, f(x,y)=arctg![]() .Sa se calculeze derivatele partiale de ordinul
intai si doi si df(-1,2), df(-1,2)(3,-2); d2f(-1,2);d2f(-1,2)(3,-2).
.Sa se calculeze derivatele partiale de ordinul
intai si doi si df(-1,2), df(-1,2)(3,-2); d2f(-1,2);d2f(-1,2)(3,-2).
Sa se calculeze derivatele partiale de ordinul intai si doi ale functiilor:
a)
f(x,y)=xy+![]() , definita pe multimea A=;
, definita pe multimea A=;
b)
f(x,y)=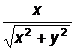 , definita pe multimea A=R2;
, definita pe multimea A=R2;
c)
f(x,y,z)=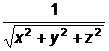 , definita pe multimea A=R3;
, definita pe multimea A=R3;
d) f(x,y)=arctg![]() , definita pe multimea A=;
, definita pe multimea A=;
e) f(x,y)=ln (x+y2), definita pe multimea A=;
f) f(x,y,z)=![]() +zln(x+y), definita pe multimea A=.
+zln(x+y), definita pe multimea A=.
Sa se afle extremele functiilor: f:D R
a) f(x,y)=xy2ex-y ;
b) f(x,y)=xy(x+y-3) ;
c)
f(x,y)=xy+![]() ;
;
d) f(x,y)=xy ln(x2+y2) ;
e) f(x,y,z)=x3+y2+z2+12xy+2z ;
f)
f(x,y,z)=x+![]() .
.
Folosind formula lui Taylor pentru functia f:D R2 R f(x,y)=xy
in jurul punctului (1,1) sa se aproximeze printr-un numar cu 3 zecimale.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |