Parcurgerea unui graf in adincime
1. Metoda generala
O a doua tehnica importanta de parcurgere a unui graf este parcurgerea in adincime (depth first search). Caracteristica definitorie a acestei tehnici este faptul ca fiecare virf este explorat in intregime imediat ce este intilnit prima data. Cu alte cuvinte, virful este vizitat si fiecare din succesorii lui este imediat procesat. Dar "procesarea" fiecarui succesor presupune aplicarea acestei tehnici in mod recursiv. Pentru a intelege modul cum opereaza aceasta tehnica, sa presupunem ca plecam din virful s. Mai intii este vizitat virful s, apoi primul succesor al acestuia (fie acesta s1) este intilnit si vizitat. In continuare consideram fiecare din succesorii lui s1; fiecare la rindul lui este vizitat si explorat cit mai adinc posibil inainte ca urmatorul succesor al lui s1 sa fie examinat. Numai dupa ce toti succesorii lui s1 (cu exceptia eventual a lui s) au fost explorati in intregime continuam cu urmatorul succesor s2 al lui s. Desigur, urmatorul succesor este posibil sa fi fost vizitat la un moment dat in explorarea lui s1, si in acest caz nu mai este examinat. Numele "depth first search" reflecta ideea ca parcurgerea avanseaza cit mai adinc posibil si mai departe de virful de plecare, avansind de la fiecare virf la succesorul acestuia, de la un succesor la succesorul acestuia, si asa mai departe, revenind pentru verificarea altor succesori numai atunci cind intilnim un virf care nu mai are succesori neexaminati si deci nu putem avansa mai departe (Larry, Denenberg, p 435-436) (Burdescu, p 54-67). In figura 1.2 avem un exemplu de parcurgere in adincime.
Intr-o parcurgere in adincime avem doua momente cind putem efectua o procedura de vizitare: un virf poate fi vizitat imediat ce este intilnit prima data, chiar inainte ca primul sau succesor sa fie procesat (asa cum am descris in paragraful precedent), sau virful poate fi vizitat dupa ce toti succesorii sai au fost explorati in intregime. Pentru a distinge aceste posibilitati definim separat procedurile PreVisit si PostVisit in conexiune cu tehnica depth first search. Aceasta tehnica se implementeaza in modul cel mai natural posibil cu ajutorul unui algoritm recursiv.
Algoritm DepthFirstSearch general;
Intrare. Un graf (X, G ) si un virf s din X.
Iesire. Informatii obtinute de procedurile de vizitare a virfurilor.
begin
for (each x I X) do Mk[x] False;
RecursivDFS(s);
end (algoritm).
Procedura RecursivDFS(virf x);
begin
Mk[x] True; PreVisit(x);
for (each y I G(x)) do
if (Mk[y] False) then RecursivDFS(y);
PostVisit(x);
end (procedura).
Este necesara o atentie deosebita la implementarea algoritmilor recursivi: trebuie identificate variabilele locale si variabilele globale, numai astfel poate fi garantata functionarea corecta a programului.
Procedura de parcurgere poate fi descrisa si iterativ - nerecursiv, cu ajutorul unui algoritm de tip back-tracking.
Procedura IterativDFS(virf s);
begin
Mk[s] True;
k 0; L[0] s; (primul virf din lista este s)
P[0] H[s]; (pozitia in S a primului succesor al virfului s)
while (k 0) do begin
j P[k]; x L[k]; (extrage un virf din lista)
PreVisit(x);
while (j < H[x 1]) do begin (x inca mai are succesori)
y S[j]; (un succesor al lui x)
if (Mk[y] = True) then j j 1;
else break; (cauta un succesor nemarcat)
end
if (j < H[x 1]) then begin
k k 1; Mk[y] True; (succesorul y se introduce in lista)
L[k] y; P[k] j; (se memoreaza si pozitia acestuia in S)
end
else begin
PostVisit(x); (x nu mai are succesori)
k k - 1;
end
end
end (procedura).
Sa comparam cele doua descrieri:
- descrierea recursiva este foarte compacta si poate fi implementata fara dificultati;
- descrierea iterativa este destul de elaborata: este dependenta de modul de reprezentare a grafului, si stiva trebuie gestionata explicit.
Exista totusi un avantaj in cazul descrierii iterative. Este mult mai simplu sa se precizeze conditii particulare de incheiere a parcurgerii, fara sa se atinga toate virfurile posibile. De exemplu, un test daca s-a atins un anumit virf poate fi plasat imediat dupa introducerea in stiva a unui succesor.
O procedura iterativa de parcurgere in adincime poate fi folosita pentru a determina un ciclu sau un lant eulerian intr-un graf neorientat (Burdescu, p 148-154).
2. Componente tare conexe
Definitia 1. Un graf orientat este tare conex daca intre orice doua virfuri exista un drum.
O componenta tare conexa a unui graf orientat este un subgraf tare conex maximal in raport cu operatia de incluziune. Cu alte cuvinte, nu exista o submultime de virfuri mai numeroasa care sa induca un subgraf tare conex.
Problema Fie un graf orientat G = (X, G ); sa se determine componentele sale tare conexe (figura 1).
Aplicatie Avem o harta rutiera a unei localitati in care X reprezinta intersectiile, si G indica pentru fiecare intersectie unde putem ajunge dupa un singur pas. Evident, nu intre oricare doua puncte de intersectie avem legaturi in ambele sensuri. Dorim sa aflam daca orice intersectie este accesibila de oriunde, sau daca nu care regiuni nu pot comunica intre ele in ambele sensuri si care intersectii fac parte din fiecare regiune.
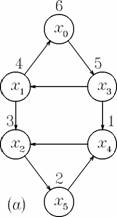
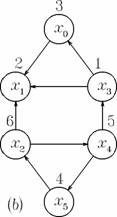
Figura 1. Ambele grafuri orientate, (a) si (b), au cite doua
componente tare conexe: si .
Virfurile sint marcate conform parcurgerii in adincime.
Algoritm CompTareConexe [cf Bur,78-84];
Intrare. Un graf orientat (X, G
Iesire. Un masiv C: componentele tare conexe ale acestuia.
begin
for (each x I X) do Mk[x] False;
Md 0;
for (each x I X) do
if (Mk[x] False) then TravMark(x);
Se ordoneaza descrescator marcajele masivului D, memorind
pentru fiecare marcaj carui virf apartine
for (each x I X) do C[x] False;
Se construieste graful invers G' corespunzator grafului G;
nc 0;
Procedura TravCnx prelucreaza graful G' astfel:
for (each x I X) do (virfurile x se iau in ordinea din masivul D)
if (C[x] 0) then begin
nc nc 1; TravCnx(x);
end
end (algoritm).
Procedura TravMark(virf x);
begin
Mk[x] True;
for (each y I G(x)) do
if (Mk[y] False) then TravMark(y);
Md Md 1; D[x] Md;
end (procedura).
Procedura TravCnx(virf x);
begin
C[x] nc;
for (each y I G(x)) do
if (C[y] 0) then TravCnx(y);
end (procedura).
Se face o prima parcurgere in adincime a grafului, si in faza de postvizitare a unui virf acesta se marcheaza cu o valoare indicind adincimea maxima care a putut fi obtinuta pornind din virful respectiv. In continuare se ordoneaza virfurile descrescator dupa valoarea acestor marcaje si se construieste graful invers corespunzator grafului de intrare: daca in graful initial exista arcul (x,y) atunci in graful inversat se insereaza arcul (y,x). In final se face o parcurgere a grafului invers (de aceasta data parcurgerea se poate face fie in adincime fie in latime), luind virfurile in ordinea descrescatoare a marcajelor obtinute in prima faza. Inainte de a doua parcurgere se ordoneaza descrescator marcajele, si in final se determina componentele tare conexe. In masivul C se memoreaza pentru fiecare virf componenta careia ii apartine.
Fiecare etapa de parcurgere a grafului necesita un timp de ordin O(n m). Etapa de ordonare a marcajelor masivului D necesita un timp de ordin O(n log n). Obtinem
Teorema 1. Determinarea componentelor tare conexe ale unui graf orientat necesita un timp de ordin O(n log n).
Am preferat, pentru simplitatea descrierii, o prezentare a algoritmului in trei faze: parcurgerea grafului initial, ordonarea marcajelor, parcurgerea grafului invers. Este posibil sa se obtina o complexitate liniara a acestui algoritm, daca se observa ca virfurile vizitate pot fi introduse intr-o stiva in ordinea executarii operatiei PostVisit. Graful invers va fi parcurs conform extragerii virfurilor din stiva astfel creata (Giumale, p 160-163).
Dintr-o lista a virfurilor marcate rezulta o componenta tare conexa sau mai multe, in functie de virfurile care pot fi atinse conform parcurgerii grafului invers. De altfel aceasta este ideea de baza a algoritmului descrisa in literatura de specialitate: se parcurge graful initial pornind dintr-un virf s, si in continuare se parcurge graful invers in ordinea precizata mai sus. Doar virfurile care pot fi atinse in ambele parcurgeri fac parte din aceeasi componenta tare conexa.
3. Biconectivitate
Definitia 4 Un virf s al unui graf neorientat este virf critic (sau virf de articulatie) daca exista doua virfuri distincte x si y orice drum elementar de la x la y trece prin s.
Definitia Un graf neorientat este biconex daca, fiind date doua virfuri distincte x si y, exista cel putin doua drumuri elementare intre ele care nu au nici un virf comun, cu exceptia celor doua capete. Cu alte cuvinte, un graf neorientat este biconex daca si numai daca nu are virfuri critice.
Exemplu. Graful din figura 2 (a) este biconex, pe cind cel din figura 2 (b) nu. Al doilea graf are doua virfuri critice: x0 si x1.
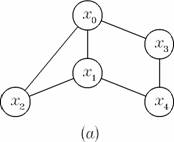
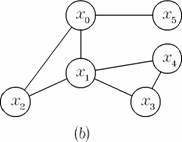
Figura 2. Un graf biconex(a); un graf cu doua virfuri critice (b). Graful
(b) admite trei componente biconexe: , si .
Problema Fie un graf neorientat G = (X, G ); sa se determine virfurile sale critice.
Aplicatie (concurs ACM, Bucuresti 1998). X reprezinta o multime de calculatoare, si G indica pentru fiecare calculator care sint calculatoarele conectate direct la acesta. Evident, fiecare conexiune este in ambele sensuri. Un calculator care corespunde unui virf critic afecteaza comunicarea in retea daca se defecteaza. In acest caz exista cel putin doua noduri, aflate in componente biconexe diferite, care nu mai pot comunica. Daca se defecteaza un calculator, fie acesta z, care nu corespunde unui virf critic, comunicarea nu este totusi afectata. Sa presupunem ca un drum care uneste doua virfuri x si y trece prin acel calculator. In acest caz, deoarece z nu este critic, se poate gasi un alt drum de la x la y care sa nu treaca prin z.
Sa se determine toate calculatoarele critice din retea.
Pentru a intelege cum trebuie aplicata tehnica depth first search in problema biconectivitatii unui graf, sa revedem algoritmul general. Consideram ca graful G este neorientat si conex. Procedura recursiva RecursivDFS proceseaza fiecare virf x marcindu-l si considerind pe rind fiecare succesor. Daca un succesor y a fost deja marcat procedura ignora pur si simplu arcul (x,y). Daca un succesor y nu a fost marcat, procedura se autoapeleaza pentru a-l procesa; spunem ca procedura avanseaza pe arcul (x,y). Sa fixam acum un virf r de start (radacina) pentru tehnica de parcurgere. Fie T graful partial care se compune din virfurile lui G si arcele de avansare; acest graf este obtinut din graful G dupa ce am eliminat arcele ignorate in timpul parcurgerii (Athanasiu et al).
Sa aratam ca T este un arbore. Intr-adevar, T contine toate virfurile din G prin definitie, si este conex deoarece orice parcurgere in adincime a grafului G (care este conex) intilneste fiecare virf din G. Mai mult, T nu contine nici un ciclu deoarece de fiecare data cind intilnim un arc ce uneste doua virfuri deja marcate acesta este ignorat si nu este adaugat la T. Putem considera ca T este un arbore cu radacina r, si un virf x este parintele lui y daca si numai daca y este primul succesor nemarcat al lui x.
Graful original G se compune din arborele T si arcele ignorate. Sa facem o observatie importanta (Larry, Denenberg, p 439-441): fiecare arc ignorat uneste doua virfuri intre care exista o relatie de ancestralitate: daca (x,y) este arc ignorat, atunci fie x este un stramos al lui y, fie y este un stramos al lui x. Pentru a vedea aceasta, fie (x,y) un arc oarecare ignorat in G, si sa presupunem ca explorarea lui x s-a terminat inainte ca explorarea lui y sa se fi terminat. Putem arata ca y trebuie sa fie un stramos al lui x; celalalt caz poate fi analizat in mod analog. Sa consideram momentul in care explorarea lui x s-a terminat. In mod cert y trebuie sa fi fost intilnit deja, altfel arcul (x,y) nu ar fi fost ignorat in timpul explorarii lui x. Dar atunci o explorare a lui y trebuie sa fie in curs de desfasurare, deoarece am presupus ca explorarea lui x se termina inainte de aceea a lui y. Aceasta explorare a lui y a fost efectuata de-a lungul unei secvente de arce de avansare de la y la x, de unde rezulta ca orice arc din G este un stramos al lui x. Deoarece fiecare arc din G este fie in T (de avansare) fie ignorat, rezulta ca orice arc din G uneste doua virfuri care se afla in relatie de ancestralitate in T. Figura 3 ilustreaza un exemplu de graf neorientat si arborele corespunzator generat de arcele de avansare selectate de parcurgerea in adincime.
Aceasta descriere a procesului de parcurgere in adincime ne conduce la o caracterizare a virfurilor critice.
Teorema 2. 1) Virful r, radacina arborelui, este virf critic daca si numai daca are mai mult de un copil in T.
2) Fie x un virf oarecare din G diferit de r. Atunci x este virf critic daca si numai daca are un copil y in T astfel incit nici un arc ignorat din G nu uneste un descendent al lui y cu un stramos propriu al lui x (diferit de el insusi).
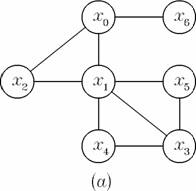
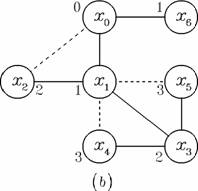
Figura Graful (a) are doua virfuri critice: x0 si x1. In urma
parcurgerii in adincime a acestuia se obtine arborele (b).
Exemplu. In figura 3 virful x0 este critic deoarece are doi copii: x1 si x6. Daca am elimina arcul (x0,x6) si am introduce arcul (x1,x6) virfurile ar fi parcurse in aceeasi ordine dar virful x0 nu ar mai fi critic deoarece singurul lui copil ar fi x1.
Virful x1 este critic deoarece unul dintre copiii lui, x3, nu are nici un descendent care sa fie unit in arbore printr-un arc cu un stramos propriu al lui x1. Pe de alta parte, x3 nu este critic deoarece arcul (x4,x1) uneste un descendent al acestuia cu un stramos propriu al lui x3; in aceeasi situatie este si arcul (x5,x1). Sa observam ca virful x1 este critic chiar daca un succesor al acestuia (x2) este unit printr-un arc cu un stramos propriu al lui x1 (x0); celalalt succesor (x3) nu are aceasta proprietate.
Faptul ca un virf y este unit cu un virf z, stramos propriu al virfului x, este reflectat de relatia D[z] < D[x] < D[y]. Figura 3 (b) indica si modul de marcare a virfurilor, valorile reprezentind adincimea relativa la virful radacina (x0).
Aceste idei sint folosite in algoritmul prezentat mai jos, care determina virfurile critice ale unui graf conex. In loc sa numerotam virfurile in ordinea in care sint intilnite, fiecare virf este marcat in masivul D cu adincimea in arborele generat de arcele de avansare plecind din r. Functia recursiva TravCritic completeaza acest masiv efectuind o parcurgere in adincime standard. Aceasta functie returneaza minimul dintre marcajele de adincime ale virfurilor intilnite in timpul explorarii complete a virfului x; pe masura ce fiecare succesor y este examinat (si probabil explorat recursiv) retinem cea mai mica dintre valorile de marcaj intilnite, inclusiv aceea returnata de functia TravCritic. Pe masura ce fiecare succesor y al lui x este explorat putem spune daca exista un descendent al lui y care sa fie adiacent cu un stramos propriu al lui x - un astfel de stramos trebuie sa aiba adincimea mai mica decit a lui x. Sa observam ca testul se aplica numai descendentilor lui x in arbore, si nu fiecarui succesor al lui x.
Dupa cum am aratat in teorema 2 radacina parcurgerii este o exceptie de la aceasta regula si este tratata separat in rutina principala.
Algoritm VirfuriCritice (Larry, Denenberg, p 442);
Intrare. Un graf neorientat conex (X, G
Iesire. Virfurile critice ale grafului, marcate True in masivul Cv.
begin
for (each x I X) do begin
Cv[x] False; D[x] 0;
end
r un virf oarecare din X;
TravCritic(r); k 0;
for (each x I G(r)) do
if (D[x] 1) then k k 1;
if (k 2) then Cv[r] True;
end (algoritm).
Functia TravCritic(virf x);
begin
md D[x];
for (each y I G(x)) do
if (D[y] 0) then begin
D[y] D[x] 1;
m TravCritic(y);
if (m D[y]) and (x r) then Cv[x] True;
md minim(m,md);
end
else md minim(md,D[y]);
return md;
end (functie).
Teorema Determinarea virfurilor critice ale unui graf neorientat necesita un timp de ordin O(n m
Algoritmul poate fi completat pentru a determina componentele biconexe astfel. Se introduc intr-o stiva gestionata explicit toate arcele de avansare pina cind se depisteaza un virf critic. In acest moment se elimina din stiva ultimele arce pina cind se depisteaza un arc care a plecat din virful depistat ca fiind critic. Toate virfurile intilnite pe parcursul eliminarii arcelor din stiva formeaza o componenta biconexa. Aceeasi procedura trebuie efectuata in mod repetat si pentru virful radacina r, daca se depisteaza ca este critic. Aceasta stiva separata poate fi organizata ca un masiv de cupluri (x,y) avind cel mult m elemente.
4. Cicluri si lanturi euleriene
Un lant (ciclu) eulerian foloseste toate muchiile o singura data.
Problema. Fiind dat un graf neorientat conex, sa se precizeze daca admite sau nu un ciclu / lant eulerian. In caz afirmativ sa se indice succesiunea de muchii a acestuia.
Aplicatie (Euler, 1736). Celebra problema a podurilor de la Königsberg era formulata astfel. Figura 4 (a) reprezinta o harta a insulei aflate pe cursul riului Pregel in localitatea Königsberg. Este posibila o plimbare astfel incit sa se traverseze toate podurile o singura data?
Figura 4 (b) este o modelare a hartii cu ajutorul unui multigraf. Intr-un multigraf putem avea mai multe muchii intre doua virfuri. O tehnica de reprezentare bazata pe functia G (liste de succesori) permite reprezentarea unui multigraf: pur si simplu un succesor este memorat de mai multe ori in lista. Intr-o matrice de adiacenta, aij va memora numarul de muchii care unesc cele doua virfuri.
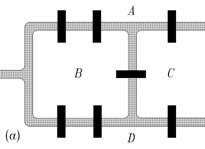
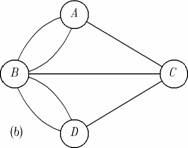
Figura 4. Podurile de la K nigsberg.
Aceasta problema poate fi generalizata astfel. Fiind data o figura geometrica construita din linii, este posibila desenarea acesteia fara sa ridicam creionul de pe hirtie si fara sa desenam de mai multe ori o linie?
Euler a dat solutia pentru problema generala intr-un articol publicat in revista Academiei de Stiinte din Petersburg: Solutio problematis ad geometriam situs pertinentis, pag 128-140.
Teorema 4. Daca un graf are n virfuri si m muchii, atunci suma gradelor tuturor virfurilor este 2m.
Demonstratie (inductie completa). Fie un graf cu n virfuri si fara muchii: suma gradelor este zero. Se adauga cite o muchie si la un moment dat avem k muchii. Presupunem ca suma gradelor este 2k. Daca mai adaugam o muchie, suma gradelor creste cu doi. n
Corolar 5. Orice graf are un numar par de virfuri de grad impar
Teorema 6. Un graf admite un lant eulerian daca si numai daca este conex (exceptind eventualele puncte izolate) si numarul virfurilor de grad impar este 0 sau 2.
Demonstratie. (T) Daca exista un lant eulerian, atunci graful este conex. Cele doua virfuri ale lantului (daca sint distincte) sint singurele care au grad impar. Deci graful nu poate avea decit 0 sau 2 virfuri de grad impar.
( ) Daca graful are o singura muchie afirmatia este evidenta. Presupunem ca afirmatia este adevarata pentru grafuri cu mai putin de m muchii. Pentru fixarea ideilor presupunem ca exista doua virfuri de grad impar: a si b (rationamentul se face la fel si pentru cazul cind nu exista virfuri de grad impar).
Un voiajor care pleaca din a intr-o directie oarecare si nu parcurge aceeasi muchie de doua ori va defini un lant m. Daca el ajunge intr-un virf x b, va utiliza un numar impar de muchii incidente cu x, deci va putea pleca pe o muchie nealeasa. Daca el ajunge in b, la un moment dat nu va mai putea pleca. In acest lant arbitrar de la a la b este posibil sa nu fie folosite toate muchiile. Ramine atunci un graf partial G' care are toate virfurile de grad par. Fie C1, C2, Ck componentele conexe ale lui G' care contin cel putin o muchie. Prin ipoteza ele admit ciclurile euleriene m1 m2 mk. Deoarece G este conex, lantul eulerian m intilneste succesiv toate componentele Ci. Sa presupunem ca ordinea este aceasta: x1 I C1, x2 I C2, xk I Ck. Sa consideram lantul m[a,x1] m1 m[x1,x2] m2 m[xk,b]. Acest lant este un lant eulerian de la a la b. n
Corolar 7. Daca un graf este conex si are 2q (q 1) virfuri de grad impar, atunci multimea arcelor sale este reuniunea a q lanturi simple disjuncte relativ la muchii (adica oricare doua lanturi distincte nu folosesc aceeasi muchie).
Demonstratie. Sa notam cu G' graful obtinut din G prin adaugarea unui nou virf z, pe care il unim prin muchii cu toate cele 2q virfuri de grad impar ale lui G. Rezulta ca G' este conex si toate virfurile sint de grad par, deci admite un ciclu eulerian. Suprimind virful z precum si toate muchiile incidente cu el, ciclul eulerian se descompune in q lanturi simple cu proprietatea enuntata mai sus. n
Din demonstratia teoremei 6 se contureaza ideea unui algoritm care sa determine un ciclu sau un lant eulerian, in cazul in care graful admite asa ceva. Se pleaca din virful a si se efectueaza o parcurgere in adincime atit timp cit acest lucru e posibil. Fiecare muchie este eliminata pe masura ce se avanseaza in graf: aceasta eliminare presupune stergerea din lista a celor doua arce gemene.
In continuare se determina, folosind un algoritm similar, cite un ciclu eulerian pentru fiecare componenta conexa rezultata. In final se insereaza toate aceste cicluri printre virfurile ciclului / lantului determinat initial, pentru a obtine un ciclu / lant eulerian. Trebuie sa folosim o tehnica adecvata pentru reprezentarea grafului, care sa permita operatii de actualizare a grafului pe masura ce acesta este parcurs: identificarea arcului geaman, stergerea unui arc.
Din pacate un astfel de algoritm poate avea un ordin mare de complexitate - cel putin O(m2), datorita necesitatii de a examina o lista de muchii pentru fiecare componenta conexa, cu scopul de a determina punctele de innodare. In continuare schitam ideea unui algoritm mai eficient, care are complexitate de ordin O(m).
Algoritm LantEulerian;
Intrare. Un graf neorientat G (X, G ) care admite un lant eulerian.
Iesire. Lista L a muchiilor in ordinea parcurgerii lantului.
begin
Fie a si b cele doua capete ale lantului (posibil a b);
r (a,0); (r este un reper pentru operatia de innodare);
L ; (organizata ca o lista simplu inlantuita)
repeat
Fie (s,p) elementele reperului r;
Parcurge in adincime graful dat plecind din s si innodind noua
lista de virfuri la pozitia p;
Fiecare virf preluat este introdus in lista L, si apoi arcul prelucrat
este eliminat din graf impreuna cu arcul invers corespunzator;
Daca in timpul parcurgerii un virf x care urmeaza sa fie introdus
in L are mai multi succesori, se memoreaza in reperul r virful
x impreuna cu pozitia pe care este memorat in lista L;
La sfirsitul parcurgerii - cind ajungem intr-o "fundatura", lantul
curent se innoada la lista L in pozitia p;
until (m 0); (oprire cind sint eliminate toate arcele din graf)
end (algoritm).
Teorema 8. Daca un graf admite un ciclu sau un lant eulerian, acesta poate fi determinat intr-un timp de ordin O(m).
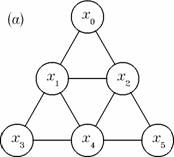
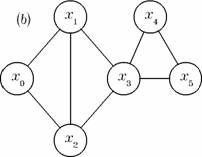
Figura 5. Grafuri euleriene.
1) Graful din figura 5 (a) admite un ciclu eulerian. O prima parcurgere da lantul (x0, x1, x2, x0). Parcurgerea s-a oprit la virful x0, si ultimele informatii memorate in r au fost despre virful x2, memorat pe pozitia a treia. Reluam parcurgerea cu virful x2 si obtinem lantul (x4, x1, x3, x4, x5, x2), care se innoada la pozitia a treia a lantului de baza. Rezulta in final ciclul (x0, x1, x2, x4, x1, x3, x4, x5, x2, x0).
2) Graful din figura 5 (b) admite un lant eulerian. O prima parcurgere da lantul (x1, x0, x2, x1, x3, x2). Parcurgerea s-a oprit la virful x2, si ultimele informatii memorate in r au fost despre virful x3, memorat pe pozitia a cincea. Reluam parcurgerea cu virful x3 si obtinem lantul (x4, x5, x3), care se innoada la pozitia a cincea a lantului de baza. Rezulta in final lantul (x1, x0, x2, x1, x3, x4, x5, x3, x2).
|
Politica de confidentialitate |
| |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |