INELE SI CORPURI
I. INTRODUCERE
Conceptele de 'inel' si 'corp' s-au sedimentat in a doua jumatate a secolului al XIX-lea prin lucrarile de teoria numerelor ale lui Dedekind, Kronecker, Weber, Hilbert. Forma definitiva a acestor notiuni este datorata lui Hilbert (1897).
II. INELE, EXEMPLE REMARCABILE, GRUPUL ELEMENTELOR
INVERSABILE AL UNUI INEL
Def.: Se numeste INEL un triplet (A,+, ) in care A este o multime nevida, iar '+' si ' ' desemneaza doua operatii pe A, numite prin extensie de limbaj 'adunare' si 'inmultire', operatii care satisfac urmatoarele trei axiome:
1) cuplul (A,+) este un grup abelian
2) cuplul (A, ) este un semigrup
3) inmultirea este distributiva fata de adunare
Daca in loc de axioma 2 apare axioma:
![]() ) cuplul (A, ) este un
monoid
) cuplul (A, ) este un
monoid
atunci tripletul (A,+, ) se numeste INEL CU ELEMENT-UNITATE.
Daca, in plus, un inel satisface si axioma:
4) inmultirea este comutativa
atunci acesta se numeste INEL COMUTATIV.
Exemple
1) ![]() inel cu
element-unitate, comutativ. Elementul nul este numarul intreg 0, iar
elementul unitate este numarul intreg 1.
inel cu
element-unitate, comutativ. Elementul nul este numarul intreg 0, iar
elementul unitate este numarul intreg 1.
2)
![]() este un inel fara element-unitate, comutativ.
Elementul nul este numarul intreg par 0.
este un inel fara element-unitate, comutativ.
Elementul nul este numarul intreg par 0.
3)
![]() ,
, ![]() ,
, ![]() ,
, ![]() sunt inele cu element-unitate (polinomul cst.1), comutative,
cu element nul (polinomul cst 0).
sunt inele cu element-unitate (polinomul cst.1), comutative,
cu element nul (polinomul cst 0).
Def.: Intr-un inel (A,+, ) cu
element-unitate, grupul ![]() al elementelor
inversabile din monoidul (A, ) se numeste
GRUPUL ELEMENTELOR INVERSABILE (GRUPUL UNITATILOR) din inelul
A.
al elementelor
inversabile din monoidul (A, ) se numeste
GRUPUL ELEMENTELOR INVERSABILE (GRUPUL UNITATILOR) din inelul
A.
Exemple
1)
In inelul ![]() avem
avem ![]()
2)
In inelul ![]() avem
avem ![]()
3) In inelul ![]() avem
avem ![]()
4)
In inelul ![]() avem:
avem: ![]()
III. DIVIZORI AI LUI ZERO, REGULI DE CALCUL, ELEMENTE INDEPENDENTE SI ELEMENTE NILPOTENTE, CARACTERISTICA
Def.: Fie (A,+, ) un inel.
1)
spunem ca un element ![]() este DIVIZOR AL LUI
ZERO LA STANGA (respectiv LA DREAPTA) daca
este DIVIZOR AL LUI
ZERO LA STANGA (respectiv LA DREAPTA) daca ![]() cu
cu ![]() (respectiv
(respectiv ![]() cu
cu ![]() )
)
Elementul ![]() se numeste DIVIZOR AL LUI ZERO daca
este divizor al lui zero la stanga sau divizor al lui zero la dreapta.
se numeste DIVIZOR AL LUI ZERO daca
este divizor al lui zero la stanga sau divizor al lui zero la dreapta.
2) spunem ca inelul A are divizori ai lui zero daca A contine cel putin un divizor al lui zero, in caz contrar, spunem ca A nu are divizori ai lui zero sau ca A este un INEL INTEGRU.
Def.: Un inel cu element-unitate, comutativ si fara divizori ai lui zero se numeste DOMENIU DE INTEGRITATE.
Exemple
1) Inelul (![]() ) are divizori
ai lui zero
) are divizori
ai lui zero
2) inelele ![]() sunt domenii de integritate,
sunt domenii de integritate, ![]() nefiind
patrat perfect
nefiind
patrat perfect
PROPOZITIE: Intr-un inel A urmatoarele afirmatii sunt echivalente:
A nu are divizori ai lui zero (A este integru)
![]()
![]()
PROPOZITIE: In orice inel A au loc egalitatile:
![]() (se spune ca zero este absorbant)
(se spune ca zero este absorbant)
2)
![]() (regula semnelor la inmultire)
(regula semnelor la inmultire)
3)
![]() (inmultirea este distributiva fata de
scadere)
(inmultirea este distributiva fata de
scadere)
PROPOZITIE: Daca A este un inel cu elementul-unitate, urmatoarele afirmatii sunt echivalente:
Inelul A are cel putin 2 elemente
0
PROPOZITIE: Fie A un inel cu element-unitate si 0 1. Atunci:
1) Elementul nul 0 nu este inversabil, adica ![]()
2) Daca ![]() atunci
si
atunci
si ![]()
PROPOZITIE: Fie A un inel cu element-unitate.
Daca elementul ![]() este inversabil, atunci x nu este divizor al
lui zero (daca x este divizor al lui zero, atunci x este neinversabil).
este inversabil, atunci x nu este divizor al
lui zero (daca x este divizor al lui zero, atunci x este neinversabil).
PROPOZITIE: Fie A un inel integru. Pentru
oricare trei elemente ![]() cu
cu ![]() avem echivalentele:
avem echivalentele:
1) ![]()
![]()
Def.: Fie A un inel.
1)
un element ![]() cu proprietatea
cu proprietatea ![]() s.n. element idempotent al lui A
s.n. element idempotent al lui A
2)
un element ![]() cu proprietatea
cu proprietatea![]() a.i.
a.i. ![]() s.n. element
nilpotent al lui A
s.n. element
nilpotent al lui A
Exemple
1)
In inelul ![]() sunt elemente idem potente, cum ar fi:
sunt elemente idem potente, cum ar fi: ![]()
2) In inelul ![]() exista un element nilpotent:
exista un element nilpotent: ![]()
PROPOZITIE: Fie A un inel. Atunci:
1) Orice element nilpotent nenul din A (daca exista) este divizor al lui zero.
2) Daca A este un inel cu element-unitate, orice element idempotent din A, diferit de 0 si 1 (daca exista), este un divizor al lui zero.
CONSECINTA: Intr-un inel cu element integru, singurul element nilpotent este 0; daca, in plus, inelul integru este cu element-unitate, singurele elemente idempotente sunt 0 si 1
PROPOZITIE: Fie A un inel cu element-unitate si
![]() un
element nilpotent. Atunci elementele
un
element nilpotent. Atunci elementele ![]() si
si
![]() sunt inversabile
sunt inversabile
Def.: Fie A un inel cu element-unitate.
1)
Daca ![]() cu
proprietatea
cu
proprietatea ![]()
![]() cel
mai mic n
cel
mai mic n
cu aceasta proprietate se numeste CARACTERISTICA inelului 1 in grupul (A,+).
2)
In caz contrar, adica ![]() spunem
ca inelul A are caracteristica 0.
spunem
ca inelul A are caracteristica 0.
Exemplu: Inelele ![]() au
caracteristica 0.
au
caracteristica 0.
PROPOZITIE
Intr-un inel integru cu element-unitate, caracteristica inelului este 0 sau un numar prim.
Propozitia lui Hilbert: Fie (A,+, ) un triplet alcatuit din multimea nevida A si operatiile de adunare '+', si de inmultire, ' * ', pe A, care satisfac axiomele:
1) (A,+) este grup
2) (A, ) este monoid
3) inmultirea este bijectiva fata de adunare
Atunci adunarea este comutativa, deci (A,+, ) este un inel cu element-unitate.
IV. CORPURI, EXEMPLE
Def.: Se numeste CORP un triplet (K,+, ) in care K este o multime cu cel putin 2 elemente, iar '+' si ' ' doua operatii pe K (numite adunare, respectiv inmultire), satisfacand urmatoarele axiome:
1) (K,+) este un grup abelian, cu element neutru 0
2) (K, ) este un grup, cu elementul neutru 1
3) Inmultirea este distributiva fata de adunare
Grupul (K,+) se numeste GRUPUL ADITIV al corpului, iar grupul (K, ) se numeste GRUPUL MULTIPLICATIV AL ELEMENTELOR NULE ale corpului.
Daca, in plus, este satisfacuta si axioma:
4) Inmultirea este comutativa, atunci tripletul (K,+, ) se numeste CORP COMUTATIV
Def.: Se numeste CORP un inel (K,+, ) cu
element-unitate, in care ![]() (echivalent spus, avand cel putin 2
elemente) si in care orice element nenul este inversabil (echivalent spus,
(echivalent spus, avand cel putin 2
elemente) si in care orice element nenul este inversabil (echivalent spus,
![]()
Exemple: (Q,+, ); (R,+, ); (C,+, ) sunt corpuri comutative.
PROPOZITIE Inelul (![]() ) al
claselor de resturi modulo-n este corp daca si numai daca n este
numar prim.
) al
claselor de resturi modulo-n este corp daca si numai daca n este
numar prim.
Expresiile formale ![]() cu
cu ![]() se numesc CUATERNIONI.
se numesc CUATERNIONI.
Notam cu H multimea cuaternionilor.
PROPOZITIE
Tripletul (H,+, ) este un corp necomutativ numit CORPUL CUATERNIONILOR.
Def.: Un polinom nenul ![]() se numeste POLINOM UNITAR (MONIC)
daca are coeficientul termenului de grad maxim egal cu 1.
se numeste POLINOM UNITAR (MONIC)
daca are coeficientul termenului de grad maxim egal cu 1.
Def.:
Un numar complex x se numeste INTREG ALGEBRIC daca
este radacina a unui polinom unitar cu coeficienti intregi,
adica daca verifica o ecuatie de forma: ![]()
Un numar complex x se numeste NUMAR ALGEBRIC daca
este radacina a unui polinom nenul cu coeficienti rationali,
adica daca verifica o ecuatie de forma: ![]()
Exemple
1)
![]() x verifica
x verifica ![]() - intreg algebric.
- intreg algebric.
2) ![]() x verifica
x verifica ![]() - numar algebric.
- numar algebric.
Obs.: Orice intreg algebric este un numar algebric.
Teorema: Tripletul![]() este
un inel comutativ cu element-unitate, numit INELUL INTREGILOR ALGEBRICI.
este
un inel comutativ cu element-unitate, numit INELUL INTREGILOR ALGEBRICI.
Teorema: Tripletul ![]() este un corp comutativ, numit CORPUL
NUMERELOR ALGEBRICE.
este un corp comutativ, numit CORPUL
NUMERELOR ALGEBRICE.
V. LEGATURA DINTRE CORPURI SI INELE INTEGRE, CORPUL FRACTIILOR UNUI DOMENIU DE INTEGRITATE
PROPOZITIE Orice corp este un inel integru, adica fara divizori ai lui zero.
Consecinta: Caracteristica unui corp este 0 sau un numar prim.
PROPOZITIE: Fie A un inel finit cu
element-unitate si ![]() . Urmatoarele
afirmatii sunt echivalente:
. Urmatoarele
afirmatii sunt echivalente:
1) A este un corp
2) A este un inel integru
Expresiile formale de tipul ![]() cu
cu ![]() se
numesc FRACTII PESTE A sau FRACTII CU NUMARATORUL
SI NUMITORUL DIN A:
se
numesc FRACTII PESTE A sau FRACTII CU NUMARATORUL
SI NUMITORUL DIN A: ![]()
PROPOZITIE: Cu notatiile de mai inainte, tripletul (K,+, ) este un corp comutativ care include inelul A, numit CORPUL FRACTIILOR LUI A.
Exemplu: Corpul de fractii al domeniului de
integritate ![]() este corpul
este corpul ![]()
VI. SUBINELE SI SUBCORPURI
Def.: Fie (A,+, ) un inel si B o submultime nevida a lui A. Spunem ca B este un SUBINEL al lui A daca B este o parte stabila fata de operatiile din A si impreuna cu operatiile induse este un inel.
Obs.: Daca (A,+, este un inel iar B A, rezulta ca B este un subinel al lui A daca si numai daca sunt indeplinite conditiile:
1) (B,+) este subgrup al grupului (A,+)
2) (B, ) este subsemigrup al semigrupului (A,
Exemple
1)
![]() este
un subinel al lui (Z[i],+,
este
un subinel al lui (Z[i],+,
2)
(3Z,+, ) este un subinel al lui ![]()
3)
(![]() ) este
un subinel al lui (
) este
un subinel al lui (![]()
4) orice inel A are cel putin doua
subinele si anume![]() si
A, numite subinele IMPROPRII; orice alt subinel (daca exista)
se numeste PROPRIU.
si
A, numite subinele IMPROPRII; orice alt subinel (daca exista)
se numeste PROPRIU.
Def.: Fie A un inel cu elementul-unitate ![]() , iar
B un subinel al lui A. Spunem ca B este SUBINEL UNITAR al lui A,
daca B are element-unitate
, iar
B un subinel al lui A. Spunem ca B este SUBINEL UNITAR al lui A,
daca B are element-unitate ![]() si acesta coincide cu cel din A,
adica
si acesta coincide cu cel din A,
adica ![]()
Obs.: Daca A este un inel cu element-unitate,
iar ![]() , rezulta
ca B este un subinel unitar al lui A daca si numai daca
sunt indeplinite conditiile:
, rezulta
ca B este un subinel unitar al lui A daca si numai daca
sunt indeplinite conditiile:
1)(B,+) este un subgrup al grupului (A,+).
2)(B, ) este un submonoid unitar al monoidului (A,
Exemple
1)
![]() este un subinel unitar al lui
este un subinel unitar al lui ![]()
2)
![]() este un subinel neunitar al lui
este un subinel neunitar al lui![]()
Teorema: Fie (A,+, ) un inel (respectiv un inel cu element-unitate) iar B o submultime nevida a lui A. Urmatoarele afirmatii sunt echivalente:
1) B este un subinel (respectiv un subinel unitar) al lui A
2) ![]() - respectiv:
- respectiv: ![]() si
si ![]()
Def.: Fie (K,+, ) un corp si L o submultime nevida a lui K. Spunem ca L este un SUBCORP al lui K daca L este o parte stabila fata de operatiile din K si relativ la operatiile induse este un corp.
Exemple
1)
![]() este un subcorp al lui
este un subcorp al lui![]()
2) Corpul patratic ![]() este subcorp al lui
este subcorp al lui ![]() iar cand
iar cand
![]() este si subcorp al lui
este si subcorp al lui ![]()
Obs.: Fie ![]() un corp si
un corp si ![]() . Atunci,
L este subcorp al lui K daca si numai daca sunt indeplinite conditiile:
. Atunci,
L este subcorp al lui K daca si numai daca sunt indeplinite conditiile:
1) ![]() este subgrup al grupului
este subgrup al grupului ![]()
2) ![]() este subgrup al grupului
este subgrup al grupului ![]() unde am notat
unde am notat ![]()
Teorema: Fie ![]() un corp si L o submultime nevida
a lui K. Urmatoarele afirmatii sunt echivalente:
un corp si L o submultime nevida
a lui K. Urmatoarele afirmatii sunt echivalente:
1) ![]() este subgrup al lui
este subgrup al lui ![]()
2) ![]() si
si ![]()
Obs.: Daca L este un subgrup al unui corp K, atunci L este subinel unitar al lui K.
PROPOZITIE Fie A un domeniu de integritate si L un corp care in include pe A ca subinel. Atunci L include corpul de fractii K al lui A. Echivalent spus, corpul de fractii al unui domeniu de integritate este cel mai mic corp ce contine inelul respectiv.
VII. IDEALE, INEL-FACTOR
Def.: Fie (A,+, ) un inel. O submultime
nevida ![]() se numeste IDEAL STANG (respectiv IDEAL DREPT) al inelului A daca
indeplineste conditiile:
se numeste IDEAL STANG (respectiv IDEAL DREPT) al inelului A daca
indeplineste conditiile:
1) ![]()
2) ![]()
O submultime ![]() care este atat ideal stang cat si ideal
drept se numeste INEL BILATERAL.
care este atat ideal stang cat si ideal
drept se numeste INEL BILATERAL.
Exemple
1) In inelul![]() orice
submultime i=nZ, cu nZ, este un ideal bilateral
orice
submultime i=nZ, cu nZ, este un ideal bilateral
2) In orice inel A, submultimile si A sunt ideal bilaterale, numite IDEALE IMPROPRII
Obs.: Intr-un inel comutativ orice ideal este bilateral si este un subinel al inelului respectiv
PROPOZITIE: Singurele ideale ale unui corp K sunt si A.
Teorema: Fie A un inel si ![]() un
ideal bilateral al inelului A. Atunci:
un
ideal bilateral al inelului A. Atunci:
1) Tripletul (A/i,+, ) este un inel, care se numeste INELUL - FACTOR (INELUL-CAT) AL LUI A prin idealul bilateral
2) Daca A este un inel cu element-unitate, atunci inelul-factor A/I este un inel cu element-unitate, iar daca A este un inel comutativ, atunci inelul-factor A/i este comutativ
VIII. MORFISME SI IZOMORFISME DE INELE SI CORPURI
Def.:
1) Fie ![]() si
si ![]() doua inele. O aplicatie
doua inele. O aplicatie ![]() cu proprietatile:
cu proprietatile:
a)
![]()
b)
![]()
se numeste MORFISM DE INELE.
2) Un morfism de inele de la un inel la el insusi se numeste ENDOMORFISM al inelului respectiv.
Exemplu
Fie
![]() un numar intreg. Se numeste MORFISMUL
CANONIC aplicatia:
un numar intreg. Se numeste MORFISMUL
CANONIC aplicatia:
![]() , daca este morfism de inele
, daca este morfism de inele
Def.: Fie ![]() si
si ![]() doua inele cu element-unitate. Un morfism
de inele
doua inele cu element-unitate. Un morfism
de inele ![]() cu proprietatea,
cu proprietatea, ![]() se numeste MORFISM UNITAR DE INELE
(1, respectiv
se numeste MORFISM UNITAR DE INELE
(1, respectiv ![]() ,
reprezinta elementul unitate din A, respectiv
,
reprezinta elementul unitate din A, respectiv ![]()
Exemplu: Daca ![]() este un inel cu element-unitate 1, functia
este un inel cu element-unitate 1, functia
![]() este un morfism unitar de inele.
este un morfism unitar de inele.
PROPOZITIE: Fie ![]() un morfism de inele. Atunci:
un morfism de inele. Atunci:
1) Multimea ![]() este un ideal bilateral al inelului A, numit NUCLEUL
morfismului
este un ideal bilateral al inelului A, numit NUCLEUL
morfismului ![]()
2)
![]() este injectiv daca si numai daca
este injectiv daca si numai daca
![]()
Def.:
1) Fie ![]() si
si ![]() doua corpuri. Un morfism unitar de inele
doua corpuri. Un morfism unitar de inele ![]() se numeste MORFISM DE CORPURI
se numeste MORFISM DE CORPURI
2) Un morfism de corpuri de la un corp la el insusi se numeste ENDOMORFISM al acelui corp
Exemplu ![]() este un morfism de corpuri, numit MORFISMUL-INCLUZIUNE.
este un morfism de corpuri, numit MORFISMUL-INCLUZIUNE.
PROPOZITIE: Orice morfism de corpuri este injectiv.
Def.:
1) Fie ![]() si
si ![]() doua inele. O aplicatie
doua inele. O aplicatie ![]() se numeste IZOMORFISM DE INELE daca
este morfism de inele inversabil (adica functie inversabila si
functia inversa :A' A este de asemenea morfism de inele).
se numeste IZOMORFISM DE INELE daca
este morfism de inele inversabil (adica functie inversabila si
functia inversa :A' A este de asemenea morfism de inele).
2) Un izomorfism de inele de la un inel la sine insusi se numeste AUTOMORFISM al acelui inel.
3) Daca intre doua inele A si
![]() exista (cel putin) un izomorfism de
inele spunem ca inelele sunt IZOMORFE si se scrie
exista (cel putin) un izomorfism de
inele spunem ca inelele sunt IZOMORFE si se scrie ![]()
Exemple ![]() este un automorfism al inelului
este un automorfism al inelului ![]()
PROPOZITIE: Fie ![]() un izomorfism de inele. Daca unul din
inelele A sau
un izomorfism de inele. Daca unul din
inelele A sau ![]() are element-unitate, atunci si celalalt
inel are element-unitate, iar izomorfismul
are element-unitate, atunci si celalalt
inel are element-unitate, iar izomorfismul ![]() este un morfism unitar de inele.
este un morfism unitar de inele.
Def.:
1) Fie ![]() si
si ![]() doua corpuri. Un izomorfism de inele
doua corpuri. Un izomorfism de inele ![]() se numeste IZOMORFISM DE CORPURI
se numeste IZOMORFISM DE CORPURI
2) Un izomorfism de la un corp la el insusi se numeste AUTOMORFISM al acelui corp
3) Daca intre doua corpuri ![]() si
si ![]() exista un izomorfism, spunem ca ele
sunt IZOMORFE si scriem
exista un izomorfism, spunem ca ele
sunt IZOMORFE si scriem ![]()
Teorema: Fie ![]() un morfism de inele (respectiv de corpuri, cand
un morfism de inele (respectiv de corpuri, cand
![]() sunt corpuri). Urmatoarele afirmatii
sunt echivalente:
sunt corpuri). Urmatoarele afirmatii
sunt echivalente:
![]() este izomorfism de inele (respectiv de
corpuri).
este izomorfism de inele (respectiv de
corpuri).
![]() este bijectiv.
este bijectiv.
Exemplu ![]() este
un automorfism al corpului
este
un automorfism al corpului ![]()
PROPOZITIE: Fie ![]() un morfism de inele (respectiv de corpuri).
Atunci:
un morfism de inele (respectiv de corpuri).
Atunci:
1) Pentru orice subinel (subcorp) B al lui A,
multimea ![]() este
un subinel (respectiv subcorp) al lui
este
un subinel (respectiv subcorp) al lui ![]() in particular multimea
in particular multimea ![]() este un subinel (subcorp) al lui
este un subinel (subcorp) al lui ![]()
2) Daca![]() este
morfism injectiv, A este izomorf cu un subinel ( respectiv subcorp) al lui B
este
morfism injectiv, A este izomorf cu un subinel ( respectiv subcorp) al lui B
Consecinta:
Daca ![]() este un morfism de corpuri, corpul K este
izomorf cu un subcorp al corpului
este un morfism de corpuri, corpul K este
izomorf cu un subcorp al corpului ![]()
Teorema fundamentala de izomorfism la inele: Fie ![]() un morfism de inele. Atunci:
un morfism de inele. Atunci:
1)
Exista un izomorfism canonic de inele ![]()
2)
Daca ![]() este un morfism surjectiv,
este un morfism surjectiv, ![]()
IX. INELE DE MATRICI PATRATICE
PROPOZITIE: Fie A un inel comutativ cu element-unitate in
care ![]() .
Atunci:
.
Atunci:
1) Tripletul ![]() este
un inel cu element-unitate, numit INELUL MATRICELOR PATRATICE DE ORDIN N
PESTE INELUL A
este
un inel cu element-unitate, numit INELUL MATRICELOR PATRATICE DE ORDIN N
PESTE INELUL A
2) Pentru ![]() ,
inelul
,
inelul ![]() este
necomutativ si are divizori ai lui zero
este
necomutativ si are divizori ai lui zero
PROPOZITIE: Matricea ![]() este inversabila in inelul
este inversabila in inelul ![]() daca si numai daca
daca si numai daca ![]() este un element inversabil in inelul A. Altfel
spus, grupul elementelor inversabile din inelul
este un element inversabil in inelul A. Altfel
spus, grupul elementelor inversabile din inelul ![]() este:
este: ![]()
Def.: Grupul multiplicativ ![]() al matricilor inversabile peste inelul A se
numeste GRUPUL LINIAR DE ORDINUL N PESTE INELUL A si se
noteaza
al matricilor inversabile peste inelul A se
numeste GRUPUL LINIAR DE ORDINUL N PESTE INELUL A si se
noteaza ![]() Asadar
Asadar
![]()
Consecinta: Pentru un corp comutativ K avem: ![]()
Exemplu: Matricea X este inversabila, 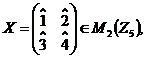 intrucat
intrucat ![]()
X. INELE DE POLINOAME
Obs.: Pentru orice ![]() avem inegalitatile:
avem inegalitatile:
1)
![]()
2)
![]()
PROPOZITIE: Multimea ![]() ,
inversata cu operatiile de adunare si inmultire a
polinoamelor este un inel comutativ cu element-unitate, numit INELUL
POLINOAMELOR PESTE INELUL A.
,
inversata cu operatiile de adunare si inmultire a
polinoamelor este un inel comutativ cu element-unitate, numit INELUL
POLINOAMELOR PESTE INELUL A.
Obs.: Inelul A este un subinel unitar al inelului
de polinoame ![]()
PROPOZITIE Inelul ![]() este domeniu de integritate daca si
numai daca inelul A este domeniu de integritate si in acest caz avem
relatia gradelor la inmultire:
este domeniu de integritate daca si
numai daca inelul A este domeniu de integritate si in acest caz avem
relatia gradelor la inmultire:
![]()
PROPOZITIE
1) Daca A este un domeniu de
integritate, avem ![]() egalitatea
care exprima faptul ca polinoamele inversabile din inelul
egalitatea
care exprima faptul ca polinoamele inversabile din inelul ![]() sunt exact elementele inversabile din A
sunt exact elementele inversabile din A
2) In caz particular, daca ![]() corp comutativ,
avem
corp comutativ,
avem ![]() egalitate
care arata ca polinoamele inversabile din
egalitate
care arata ca polinoamele inversabile din ![]() sunt constantele nenule din K, adica
polinoamele de grad zero
sunt constantele nenule din K, adica
polinoamele de grad zero
Exemplu
1)
![]()
2) ![]()
Def.: Daca A este un domeniu de integritate,
corpul functiilor domeniului de integritate ![]() se numeste CORPUL FRACTIILOR
RATIONALE peste inelul A si se noteaza
se numeste CORPUL FRACTIILOR
RATIONALE peste inelul A si se noteaza ![]()
Fractiile rationale peste A
sunt de forma: ![]()
Def.: Fie A un inel comutativ cu element-unitate
si ![]() iar
iar ![]()
![]() un polinom.
un polinom.
1) Daca ![]() atunci elementul
atunci elementul ![]() IA se numeste VALOAREA
POLINOMULUI F IN PUNCTUL X.
IA se numeste VALOAREA
POLINOMULUI F IN PUNCTUL X.
2) Daca ![]() spunem ca
spunem ca ![]() se anuleaza in punctul x sau ca x
este o radacina a polinomului
se anuleaza in punctul x sau ca x
este o radacina a polinomului ![]() in inelul A.
in inelul A.
3) Functia ![]() deci functia care asociaza fiecarui
deci functia care asociaza fiecarui ![]() valoarea polinomului
valoarea polinomului ![]() in punctul x se numeste FUNCTIA
POLINOMIALA asociata polinomului
in punctul x se numeste FUNCTIA
POLINOMIALA asociata polinomului ![]()
Obs.: Daca doua polinoame sunt egale,
atunci si functiile lor polinomiale sunt egale, adica: ![]()
Lema: Fie A un domeniu de integritate si![]() un
polinom de grad cel mult n. Daca
un
polinom de grad cel mult n. Daca ![]() are (cel putin) n+1 radacini
distincte in inelul A, atunci este polinomul nul.
are (cel putin) n+1 radacini
distincte in inelul A, atunci este polinomul nul.
PROPOZITIE: Fie ![]() doua
polinoame de grad cel mult n astfel incat
doua
polinoame de grad cel mult n astfel incat ![]() Daca A este un domeniu de integritate cu
mai mult de n elemente (in particular, A poate fi infinit atunci
Daca A este un domeniu de integritate cu
mai mult de n elemente (in particular, A poate fi infinit atunci ![]()
Def.: Fie ![]() (corp comutativ) doua polinoame.
(corp comutativ) doua polinoame.
1) Spunem ca g divide sau
ca se divide cu g, daca ![]() Scriem
Scriem ![]() (citim g divide sau citim se divide cu g).
(citim g divide sau citim se divide cu g).
2) Spunem ca
si g
sunt asociate in divizibilitate daca se divid reciproc, adica ![]()
3) Spunem ca polinoamele f
si g au cel mai mare divizor
comun (c.m.m.d.c) ![]() daca exista polinomul
daca exista polinomul ![]() satisfacand conditiile:
satisfacand conditiile:
i) d este divizor comun pentru si
g, adica ![]()
ii) Orice alt divizor
comun pentru si g
il divide pe d, adica ![]() cu
cu ![]() si
si
![]()
Notam cu ![]() c.m.m.d.c. al
polinoamelor si g. Scriem
c.m.m.d.c. al
polinoamelor si g. Scriem![]()
![]() a.i.
a.i. ![]() Observam ca.
Observam ca.
PROPOZITIE: Doua polinoame sunt asociate daca si numai daca difera printr-un factor inversabil (polinom de gradul zero).
Teorema impartirii cu rest
Fie ![]() cu
cu ![]() Exista
atunci alte doua polinoame
Exista
atunci alte doua polinoame ![]() cu
proprietatile:
cu
proprietatile:
1)
![]()
2)
![]()
![]()
Polinoamele ![]() se numesc deimpartit, impartitor,
cat respectiv rest, remarcam ca impartitorul
trebuie sa fie nenul.
se numesc deimpartit, impartitor,
cat respectiv rest, remarcam ca impartitorul
trebuie sa fie nenul.
Teorema lui Bezout, teorema restului: Fie ![]() Atunci:
Atunci:
1) Restul impartirii polinomului prin X-x este (x)
2) x este radacina pentru daca si numai daca se divide cu (X-x)
Obs.: 1) Daca
![]()
2)
Daca ![]() ,
atunci
,
atunci ![]()
Lema: Fie ![]() polinoame legate prin relatia
polinoame legate prin relatia ![]() Daca exista
Daca exista ![]() atunci exista
atunci exista ![]() si avem:
si avem: ![]()
Teorema: Fie ![]() Atunci:
Atunci:
i)
sirul de impartiri cu rest (1) este finit, adica exista
![]() a.i.
a.i. ![]()
ii) exista c.m.m.d.c. al
polinoamelor si g si acesta este ultimul rest
nenul, adica ![]() cand
cand ![]() (Cand k=1 inseamna ca prima
impartire se face exact si atunci
(Cand k=1 inseamna ca prima
impartire se face exact si atunci ![]()
Obs.: Oricare doua polinoame care reprezinta c.m.m.d.c. a doua polinoame fixate, sunt asociate in divizibilitate.
Def.: Daca ![]() spunem ca polinoamele si
g sunt relativ prime sau prime intre ele.
spunem ca polinoamele si
g sunt relativ prime sau prime intre ele.
Obs.: Exista echivalenta: ![]()
PROPOZITIE: Fie ![]() astfel incat
astfel incat ![]() iar
iar ![]() Atunci
Atunci ![]()
Def.:
1) Un polimon ![]() nenul si neinversabil (echivalent spus,
neasociat cu 0 sau 1 sau totuna, de grad
nenul si neinversabil (echivalent spus,
neasociat cu 0 sau 1 sau totuna, de grad ![]() ) se
numeste IREDUCTIBIL IN INELUL K[X] sau IREDUCTIBIL PESTE CORPUL
K daca, abstractie facand de asocieri, singurii sai
divizori in K[x] sunt 1 si p. Aceasta inseamna ca:
) se
numeste IREDUCTIBIL IN INELUL K[X] sau IREDUCTIBIL PESTE CORPUL
K daca, abstractie facand de asocieri, singurii sai
divizori in K[x] sunt 1 si p. Aceasta inseamna ca: ![]()
2) Un polinom nenul si
neinversabil care nu este ireductibil se mai numeste REDUCTIBIL in ![]()
Exemplu: In orice inel ![]() polinoamele de gradul1 sunt ireductibile.
polinoamele de gradul1 sunt ireductibile.
Lema: Fie ![]() un polinom ireductibil si
un polinom ireductibil si ![]() un polinom oarecare. Daca p nu divide , atunci
un polinom oarecare. Daca p nu divide , atunci
![]()
PROPOZITIE: Fie ![]() un polinom nenul si neinversabil. Urmatoarele
afirmatii sunt echivalente:
un polinom nenul si neinversabil. Urmatoarele
afirmatii sunt echivalente:
1)
p este ireductibil in ![]()
2)
![]()
(Asadar, un polinom este ireductibil daca si numai daca ori de cate ori divide un produs, rezulta ca divide unul din factori).
Teorema: Orice polinom nenul si neinversabil din
![]() se
descompune in mod unic intr-un produs finit de polinoame ireductibile din
se
descompune in mod unic intr-un produs finit de polinoame ireductibile din ![]() Unicitatea este inteleasa abstractie
facand de asocieri si de ordinea factorilor.
Unicitatea este inteleasa abstractie
facand de asocieri si de ordinea factorilor.
PROPOZITIE In inelul ![]() singurele polinoame ireductibile sunt cele de
gradul 1.
singurele polinoame ireductibile sunt cele de
gradul 1.
Consecinta: Orice polinom ![]() nenul si neinversabil se descompune in
mod unic in factori liniari in inelul
nenul si neinversabil se descompune in
mod unic in factori liniari in inelul ![]()
PROPOZITIE Fie ![]() un polinom de grad
un polinom de grad ![]()
i) O conditie necesara ca polinomul
p sa fie ireductibil in ![]() este ca el sa nu aiba radacini
in corpul K
este ca el sa nu aiba radacini
in corpul K
ii) Daca grad ![]() conditia
necesara de la i) este si suficienta, deci p este ireductibil daca
si numai daca nu are radacini in K.
conditia
necesara de la i) este si suficienta, deci p este ireductibil daca
si numai daca nu are radacini in K.
Exemplu: Polinomul ![]() este ireductibil, intrucat este de grad 2 si
nu are radacini in corpul
este ireductibil, intrucat este de grad 2 si
nu are radacini in corpul ![]()
PROPOZITIE: Polinoamele ireductibile din inelul
![]() sunt polinoamele de gradul 1 si polinoamele
de gradul 2 care nu au radacini in corpul
sunt polinoamele de gradul 1 si polinoamele
de gradul 2 care nu au radacini in corpul ![]()
Consecinta: Orice polinom ![]() nenul si
neinversabil, se descompune in mod unic in inelul
nenul si
neinversabil, se descompune in mod unic in inelul ![]() intr-un produs de factori liniari sau factori
de gradul 2 fara radacini reale.
intr-un produs de factori liniari sau factori
de gradul 2 fara radacini reale.
Def.: Un polinom ![]() se numeste POLINOM PRIMITIV daca c.m.m.d.c.
al tuturor coeficientilor sai este egal cu 1.
se numeste POLINOM PRIMITIV daca c.m.m.d.c.
al tuturor coeficientilor sai este egal cu 1.
PROPOZITIE
1) Orice polinom![]() se
scrie sub forma
se
scrie sub forma ![]() unde
unde ![]() iar
iar ![]() este un polinom primitiv
este un polinom primitiv
2) Orice polinom![]() se
scrie sub forma = rg, unde
se
scrie sub forma = rg, unde![]() iar
iar ![]() este un polinom primitiv.
este un polinom primitiv.
Obs.: Daca![]() este
un polinom ireductibil, atunci in mod necesar f este un polinom primitiv.
este
un polinom ireductibil, atunci in mod necesar f este un polinom primitiv.
Obs.: Fie ![]() un
polinom primitiv si
un
polinom primitiv si ![]() Daca
Daca ![]() atunci
atunci
![]()
Def.: Daca ![]() iar
iar ![]() este un numar prim fixat, polinomul
este un numar prim fixat, polinomul ![]() (unde
(unde![]() este clasa de resturi modulo-p a numarului intreg a) se numeste POLINOMUL
REDUS MODULO-P AL LUI F.
este clasa de resturi modulo-p a numarului intreg a) se numeste POLINOMUL
REDUS MODULO-P AL LUI F.
Lema lui GAUSS: Fie ![]() doua polinoame primitive. Atunci
polinomul-produs
doua polinoame primitive. Atunci
polinomul-produs ![]() este de asemenea un polinom primitiv.
este de asemenea un polinom primitiv.
Teorema lui Gauss: Daca ![]() este un polinom ireductibil in inelul
este un polinom ireductibil in inelul ![]() atunci este ireductibil si in inelul
atunci este ireductibil si in inelul ![]()
COROLAR Fie ![]() un polinom primitiv. Atunci este
ireductibil in
un polinom primitiv. Atunci este
ireductibil in ![]() daca
si numai daca este ireductibil in
daca
si numai daca este ireductibil in ![]()
Teorema lui Gauss (2): Orice polinom nenul si
neinversabil din inelul ![]() se descompune in mod unic intr-un produs finit de polinoame
ireductibile din
se descompune in mod unic intr-un produs finit de polinoame
ireductibile din ![]() unicitatea fiind inteleasa facand
abstractie de ordinea factorilor si a asocierii in divizibilitate.
unicitatea fiind inteleasa facand
abstractie de ordinea factorilor si a asocierii in divizibilitate.
Criteriul de ireductibilitate al lui
Schönemann: Fie ![]() un numar prim si
un numar prim si ![]() un polinom unitar, unde
un polinom unitar, unde ![]() iar
iar ![]() Daca
in inelul
Daca
in inelul ![]() in
in ![]() polinomul
polinomul![]() este ireductibil si nu divide polinomul
este ireductibil si nu divide polinomul![]() atunci polinomul h este ireductibil si in
atunci polinomul h este ireductibil si in ![]()
Criteriul de ireductibilitate al lui Einstein
Fie ![]() un polinom cu proprietatea ca exista
un numar prim
un polinom cu proprietatea ca exista
un numar prim ![]() astfel incat p divide toti coeficientii
astfel incat p divide toti coeficientii ![]() dar
dar ![]() nu divide termenul liber
nu divide termenul liber ![]() Atunci este ireductibil in inelul
Atunci este ireductibil in inelul ![]() deci si in inelul
deci si in inelul ![]()
Obs.: Un polinom ![]() de
grad
de
grad ![]() are in corpul K cel mult 'n' radacini, nu
neaparat distincte.
are in corpul K cel mult 'n' radacini, nu
neaparat distincte.
PROPOZITIE: Fie ![]() un polinom de grad
un polinom de grad ![]() Urmatoarele afirmatii sunt
echivalente:
Urmatoarele afirmatii sunt
echivalente:
1) Factorii liniari, presupusi nu neaparat
distincti, din descompunerea lui in factori ireductibili in inelul ![]() sunt:
sunt: ![]()
2) Radacinile polinomului in
corpul K, presupuse nu neaparat distincte,sunt ![]()
3) Exista scrierea ![]() unde
unde ![]() este un polinom care nu are radacini
in corpul K.
este un polinom care nu are radacini
in corpul K.
PROPOZITIE: (cand ![]() ): Fie
): Fie
![]() un
polinom de gradul n. Urmatoarele afirmatii sunt echivalente:
un
polinom de gradul n. Urmatoarele afirmatii sunt echivalente:
1) Polinomul se descompune in inelul ![]() intr-un produs de factori liniari, nu neaparat
distincti
intr-un produs de factori liniari, nu neaparat
distincti ![]()
2) Radacinile polinomului in
corpul K sunt ![]() presupuse nu neaparat distincte.
presupuse nu neaparat distincte.
3)
Exista egalitatea ![]()
PROPOZITIE: Fie ![]() un
polinom de grad n, care are in corpul K radacinile
un
polinom de grad n, care are in corpul K radacinile ![]() nu neaparat distincte. Atunci au loc
egalitatile:
nu neaparat distincte. Atunci au loc
egalitatile:
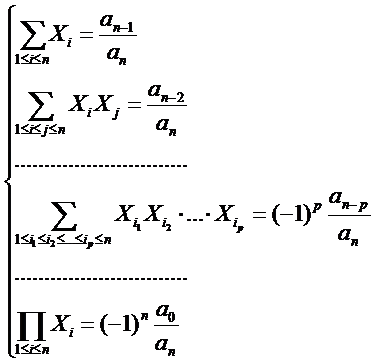
![]() Aceste inegalitati se numesc formulele
lui Vičte.
Aceste inegalitati se numesc formulele
lui Vičte.
PROPOZITIE Fie ![]() un polinom de grad n, care are in corpul K
radacinile
un polinom de grad n, care are in corpul K
radacinile ![]() multiple respectiv de ordin
multiple respectiv de ordin ![]() cu
cu ![]() .
Atunci, descompunerea lui in factori ireductibili in inelul
K[x] este
.
Atunci, descompunerea lui in factori ireductibili in inelul
K[x] este ![]() unde
unde ![]() este coeficientul dominant al polinomului
este coeficientul dominant al polinomului
XI. DESCOMPUNEREA FRACTIILOR RATIONALE PESTE UN CORP
COMUTATIV IN SUME DE FRACTII SIMPLE
Def.:
1)
Fractiile rationale de forma ![]() unde
unde ![]() este un polinom ireductibil,
este un polinom ireductibil, ![]() este un polinom cu proprietatea:
este un polinom cu proprietatea: ![]() se numesc FRACTII RATIONALE
SIMPLE.
se numesc FRACTII RATIONALE
SIMPLE.
2)
Fractiile rationale ![]() se numesc FRACTII IREDUCTIBILE.
se numesc FRACTII IREDUCTIBILE.
Lema: Fie ![]() un polinom nenul si
un polinom nenul si ![]() un
polinom oarecare. Atunci, pentru fiecare
un
polinom oarecare. Atunci, pentru fiecare ![]() natural fixat, exista si sunt unice
polinoamele
natural fixat, exista si sunt unice
polinoamele ![]()
![]() astfel incat avem scrierea:
astfel incat avem scrierea: ![]()
Lema: Daca ![]() este o fractie ireductibila, unde
este o fractie ireductibila, unde ![]() si
si ![]() exista h1, h2,., hnIK[x], cu
exista h1, h2,., hnIK[x], cu
![]() astfel
incat avem scrierea
astfel
incat avem scrierea ![]()
PROPOZITIE: Fie ![]() o fractie rationala (respectiv
o fractie rationala ireductibila) si fie
o fractie rationala (respectiv
o fractie rationala ireductibila) si fie ![]() descompunerea lui v in factori reductibili in
inelul
descompunerea lui v in factori reductibili in
inelul ![]() Atunci are loc descompunerea in suma de
fractii rationale (respectiv de fractii rationale
ireductibile) de tipul:
Atunci are loc descompunerea in suma de
fractii rationale (respectiv de fractii rationale
ireductibile) de tipul:
![]()
In plus, polinoamele ![]() sunt determinate abstractie facand
respectiv de un termen multiplu
sunt determinate abstractie facand
respectiv de un termen multiplu ![]() adica daca mai avem si scrierea
adica daca mai avem si scrierea
![]() atunci
atunci ![]() se divide cu
se divide cu ![]()
PROPOZITIE: Fie ![]() un polinom ireductibil,
un polinom ireductibil, ![]() si
si ![]() natural. Atunci fractia
natural. Atunci fractia ![]() se descompune in mod unic intr-o suma de
fractii simple si un polinom, adica:
se descompune in mod unic intr-o suma de
fractii simple si un polinom, adica: ![]()
Teorema de descompunere in fractii
simple: Fie ![]() o fractie
rationala. Presupunem ca in inelul
o fractie
rationala. Presupunem ca in inelul ![]() polinomul v are urmatoarea descompunere in
factori ireductibili:
polinomul v are urmatoarea descompunere in
factori ireductibili: ![]()
Atunci fractia ![]() se scrie in mod unic ca suma dintre un polinom
si fractii simple:
se scrie in mod unic ca suma dintre un polinom
si fractii simple:
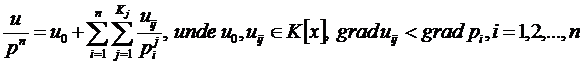
Consecinta: Daca ![]() este un morfism surjectiv de grupuri, atunci
avem izomorfismul de grupuri:
este un morfism surjectiv de grupuri, atunci
avem izomorfismul de grupuri: ![]()
Exemple 1)
![]()
2) Fie ![]() un grup oarecare cu element neutru. Atunci
un grup oarecare cu element neutru. Atunci ![]()
PROPOZITIE: Pentru orice multime finita
A cu n elemente, grupul ![]() al bijectiilor lui A este izomorf cu
grupul simetric
al bijectiilor lui A este izomorf cu
grupul simetric ![]() al permutarilor de grad n.
al permutarilor de grad n.
Def: Fie ![]() un grup in notatie multiplicativa
si
un grup in notatie multiplicativa
si ![]() fixat. Aplicatiile
fixat. Aplicatiile ![]() si
si ![]() sunt evident bijective de la G la G si se
numesc OMOTETIE LA STANGA determinata de a, respectiv OMOTETIE
LA DREAPTA determinata de a.
sunt evident bijective de la G la G si se
numesc OMOTETIE LA STANGA determinata de a, respectiv OMOTETIE
LA DREAPTA determinata de a.
Daca grupul ![]() este dat in notatie aditiva si
este dat in notatie aditiva si ![]() aplicatiile
aplicatiile ![]() se numesc TRANSLATIE LA STANGA
determinata de a, respectiv TRANSLATIE LA DREAPTA determinata
de a.
se numesc TRANSLATIE LA STANGA
determinata de a, respectiv TRANSLATIE LA DREAPTA determinata
de a.
Teorema lui Cayley: Orice grup finit este izomorf cu un subgrup al unui grup de permutari.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |