Tetraedre izodinamice si izofaciale
Definitie : Tetraedrul izodinamic este tetraedrul pentru care produsul lungimilor muchiilor opuse este constant.
Teorema 50:
Fiind dat un tetraedru [ABCD] si un punct MIInt(ABC) conditia necesara si suficienta ca dreptele ANA, BNB, CNC, DND( AM (BCD)=; gA(MA)=NA) sa fie concurente este:
 AB CD=AC BD=AD BC.
AB CD=AC BD=AD BC.
Demonstratie :
Se considera pentru inceput varfurile Asi B.
Fie QICD (ABM), PI(MNA) CD, P I(ANB) CD.
Evident dreptele ANA si BNB sunt secante daca si numai
daca punctele P si P coincid.
Aplicand teorema lui Steiner a izogonalelor in DBCD
si DACD se obtine
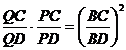 ;
; 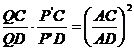 . Se constata imediat ca punctele P si P coincid daca si numai daca sunt egali membrii secunzi
ai egalitatilor evidentiale, adica: BC AD=AC BD.
. Se constata imediat ca punctele P si P coincid daca si numai daca sunt egali membrii secunzi
ai egalitatilor evidentiale, adica: BC AD=AC BD.
Inlocuind B cu C se constata , analog, ca dreptele ANA ,BNB, CNC si DND sunt secante doua cate doua , atunci are loc(1) si reciproc.
Un caz particular de tetraedru izodinamic [ABCD] este tetraedrul in acre una din fete este triunghi echilateral. Presupunand ca aceasta fata este (ABC) , in afara egalitatii (1) vor avea loc
(AB)s(BC)s(CA) (2) si (AD)s(BD)s(CD) (3).
Un astfel de tetraedru se numeste izofacial sau mai frecvent piramida triunghiulara regulata.
Teorema 51:
Un tetraedru izodinamic [ABCD] este izofacial daca si numai daca este ortocentric.
Demonstratie :
Ipoteza ca [ABCD] este izodinamic asigura ca, dup[a fixarea etalonului pentru masurarea lungimilor , exista un numar real pozitiv p, astfel incat pentru orice pereche de mucii opuse lungimilor lor x,y sa satisfaca egalitatea x y=p.
Conform relatiilor tetraedrului ortocentric AC2 + BD2 = CD2 +AB2 = BC2 +AD2 revine la existenta lui k in R astfel incat x2 + y2=k . Asadar x si y sunt solutiile ecuatiei de gradul al II-lea
![]() .
.
Daca aceasta ecuatie are radacini confundate se obtine imediat ca [ABCD] are toate muchiile congruente, deci este si izofacial.
Daca ecuatia considerata are radacini distincte t1 si t2 urmeaza =. Se poate presupune ca notarea tetraedrului s-a facut astfel incat (AB)s(BC)=t1 si (AD)s(CD)=t2.
Urmeaza explicitarea egalitatii de multimi =.
Daca AC=t1 si BD=t2 atunci se obtin egalitatile (2) si (3). Daca AC=t2 si BD=t1 se constata imediat ca au loc relatiile :
(AD)s(DC)s(CA) si (3 (AB)s(BC)s(BD) ce difera de (2) si (3) doar prin modul de notare.
Deci , daca tetraedrul izodinamic [ABCD] este ortocentric atunci el este izofacial.
Reciproc , daca tetraedrul [ABCD] este izofacial , din egalitatile (2) si (3) T AC2 + BD2 = CD2 +AB2 = BC2 +AD2 si care asigura ca tetraedrul [ABCD] este ortocentric.
Teorema 52:
Un tetraedru izodinamic [ABCD] este izofacial daca si numai daca este tetraedru Crelle.
Demonstratia se obtine din cea precedenta ,inlocuind formula AC2 + BD2 = CD2 +AB2 = BC2 +AD2 cu AD+BC=AC+BD=AB+CD.
Teorema 53:
Un tetraedru [ABCD] este izodinamic daca si numai daca
![]()
Demonstratie :
Folosind teorema lui Bretschneider(1870) pentru un tetraedru [ABCD] au loc egalitatile:
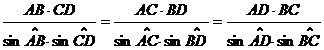
Aplicand aceasta teorema , relatia (4) este echivalenta cu (1) :AB CD=AC BD=AD BC.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |