Relatii binare pe o multime
Definitia 2.1. Numim relatie
binara pe multimea M orice submultime a produsului cartezian M ![]() M.
M.
Vom nota prin Rel (M) multimea relatiilor binare ale lui M.
Relatiile DM (numita si diagonala
produsului cartezian M![]() M), ca si M = M
M), ca si M = M![]() M fac parte din Rel
(M); orice relatie din Rel (M) diferita de DM si M se zice netriviala.
M fac parte din Rel
(M); orice relatie din Rel (M) diferita de DM si M se zice netriviala.
Pentru r I Rel (M) definim :
r si
r r (r r se zice compunerea relatiilor r si r ). Se verifica imediat ca (Rel(M), ) este monoid in care elementul neutru este DM r~ nu este inversul lui r fata de compunerea relatiilor binare
Pentru ![]() Rel(M) si n
Rel(M) si n![]() Z definim:
Z definim:
daca n>0 daca n<0 daca n=0
![]()
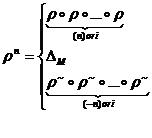
Daca m, n I![]() si r I Rel (M) atunci ( rm)n = rm·n iar rm rn rm+n. De asemenea, daca r r I Rel (M) si r r , atunci r
si r I Rel (M) atunci ( rm)n = rm·n iar rm rn rm+n. De asemenea, daca r r I Rel (M) si r r , atunci r![]() r )~ si r d r d pentru orice d I Rel (M) iar (r d d p
r )~ si r d r d pentru orice d I Rel (M) iar (r d d p
Definitia 2.2. Fie r I Rel (M). Vom spune despre r ca este:
i) reflexiva daca DM r
ii) simetrica daca r r
iii) antisimetrica
daca r ![]() r DM
r DM
iv) tranzitiva daca r r
v) totala daca r ![]() r M
r M
O relatie r IRel (M) care este simultan reflexiva, simetrica si tranzitiva se zice relatie de echivalenta pe M. Vom nota prin Echiv(M) multimea relatiilor de echivalenta de pe M; evident Echiv (M) Rel (M).
Daca r IEchiv (M), atunci r r si r![]() = r iar daca (ri)iII este o familie de relatii de
echivalenta de pe M, atunci
= r iar daca (ri)iII este o familie de relatii de
echivalenta de pe M, atunci ![]() ri IEchiv (M).
ri IEchiv (M).
Propozitia 2.3.
Fie r![]() , r
, r![]() I Echiv (M). Atunci:
I Echiv (M). Atunci:
i) r![]() r
r![]() I Echiv(M) daca si
numai daca r
I Echiv(M) daca si
numai daca r![]()
![]() r
r![]() = r
= r![]()
![]() r
r![]()
ii) r![]()
![]() r
r![]() I Echiv
(M) daca si numai daca r
I Echiv
(M) daca si numai daca r![]()
![]() r
r![]() , r
, r![]()
![]() r
r![]() r
r![]()
![]() r
r![]() Demonstratie:
Demonstratie:
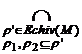 ρ′ .
ρ′ . r r ) ˛ = r r r r r r g
Propozitia 2.4. Fie r I Rel (M) si q DM r r . Atunci :
i) q este cea mai mica relatie reflexiva si simetrica ce contine pe r
ii) ![]() =
= ![]() q
q![]() este
cea mai mica relatie de echivalenta ce contine pe r
este
cea mai mica relatie de echivalenta ce contine pe r
(deci
![]() este relatia de echivalenta
generata de r
este relatia de echivalenta
generata de r
Demonstratie:
i) Evident r q iar daca r este o alta relatie reflexiva si simetrica astfel incat r r atunci, cum DM r si r r r deducem ca q r
ii)
Din i) deducem ca q este reflexiva si simetrica.
Cum (q![]() )
)![]() q
q![]() )
)![]() = q
= q![]() deducem ca pentru orice nIN
deducem ca pentru orice nIN![]() q
q![]() este simetrica. Atunci rezulta imediat ca si
este simetrica. Atunci rezulta imediat ca si ![]() este
simetrica.
este
simetrica.
Pentru tranzivitate, fie (x, y), (y, z) I![]() .
Exista deci m, n I N
.
Exista deci m, n I N![]() astfel incat (x, y) I rm si (y, z) I rn. Atunci (x, y) I r
astfel incat (x, y) I rm si (y, z) I rn. Atunci (x, y) I r![]() r
r![]() r
r![]()
![]() si acum totul
este clar. g
si acum totul
este clar. g
Definitia 2.5. Fie rIEchiv (M) si x I M. Multimea x r poarta numele de clasa de echivalenta a lui x relativa la r (sau modulo r), iar M r poarta numele de multimea cat (sau factor) a lui M prin r
Propozitia 2.6. Fie r I Echiv (M). Atunci:
i) x I x r
ii) ![]() (x r M
(x r M
iii) x r y r daca si numai daca (x, y) Ir
iv) Daca x yIM, atunci x r y r sau (x r (y r
Aplicatia p![]() :
M M r p
:
M M r p![]() x x r pentru orice xIM poarta numele de surjectia
canonica a lui M pe
multimea factor M r
x x r pentru orice xIM poarta numele de surjectia
canonica a lui M pe
multimea factor M r
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |