
Relatii de congruenta. Teoremele de izomorfism
Definitia 1. Fie A o algebra de tip t = ( n1, n2, , no (t
Numim relatie de congruenta pe A orice relatie q I Echiv (A ) ce verifica asa zisa proprietate de substitutie :
Pentru fiecare i I , daca ( aj, aj I q pentru j = 1, 2, ni, atunci (fi (a1,
![]() ), fi (a
), fi (a ![]() ))I q
))I q
Vom nota prin Con (A) multimea congruentelor lui A (evident DA A I Con(A))
Exemplu. Fie A, B algebre de acelasi tip t iar f I Hom (A, B). Nucleul lui f, notat prin Ker(f) se defineste ca fiind relatia binara de pe A:(a, a IKer(f) f(a)=f(a
Propozitia Daca f I Hom (A, B) atunci Ker (f) I Con (A).
Demonstratie:
Fie 1 i t) si ( aj, a j I Ker (f) pentru 1 j ni ; atunci f(aj)=f(a j Deducem imediat ca fi(f
(a1), , f (![]() )) = fi(f(a′1), , f(
)) = fi(f(a′1), , f(![]() f(fi(a1,
f(fi(a1, ![]() ))=f(fi(a1,
))=f(fi(a1, ![]() (fi(a1,
(fi(a1, ![]() ), fi(a′1,
), fi(a′1, ![]() IKer (f), adica Ker (f) I Con
(A).g
IKer (f), adica Ker (f) I Con
(A).g
Teorema 3. Pentru orice algebra A, (Echiv (A), ) este latice completa iar Con (A) este sublatice completa a lui Echiv (A).
Demonstratie: Evident (Echiv (A), ) este latice deoarece pentru r r IEchiv(A), r r r r I Echiv (A) iar r r relatia de echivalenta generata de r r Descrierea lui r r este data de: ( ai b ) I r r daca si numai daca exista un sir de elemente a1, a2, , an I A astfel incat a = a1, b = an iar pentru orice 1 i n - 1 , ( ai, ai+1 ) I r sau ( ai, ai+1 ) I r
Mai mult, Echiv (A) este latice
completa deoarece pentru o familie (qi)iII de elemente din Echiv (A), ![]() q i =
q i = ![]() qi iar
qi iar![]() qi
qi
Deoarece intersectia unei familii oarecare de relatii de congruenta de pe A este de asemenea o congruenta pe A deducem ca Con (A) este inf - semilatice completa si totodata inf - sublatice a lui Echiv (A).
Fie acum (qi)iII o familie de relatii de congruenta
de pe A iar f o operatie n-ara pe A. Daca (a1, b1), , (an, bn) I![]() q i, atunci putem gasi i0, i1, , ik I I astfel incat (ai, bi) I
q i, atunci putem gasi i0, i1, , ik I I astfel incat (ai, bi) I ![]()
![]()
![]()
![]()
![]()
![]() i n), de unde (f(a1, , an), f( b1, , bn)) I
i n), de unde (f(a1, , an), f( b1, , bn)) I ![]()
![]()
![]()
![]()
![]()
![]() adica
adica
![]() q i I Con (A), deci Con (A) este si sublatice sup - completa (deci
completa) a lui Echiv (A). g
q i I Con (A), deci Con (A) este si sublatice sup - completa (deci
completa) a lui Echiv (A). g
Observatie:
Deoarece orice multime ordonata A care este inf-completa este
latice completa era suficient sa probam ca Echiv (A) (ca
si Con (A)) este
inf-completa pentru a trage concluzia ca este latice completa. Am
probat si sup-completitudinea pentru a prezenta o caracterizare a lui ![]() qi cu qi I Con (A) : (x, y) I
qi cu qi I Con (A) : (x, y) I![]() qi daca si numai daca exista un sir de elemente din
A, x = a1, , an = y astfel incat pentru orice 1 j n-1, (aj, aj+1) I qi cu i I I .
qi daca si numai daca exista un sir de elemente din
A, x = a1, , an = y astfel incat pentru orice 1 j n-1, (aj, aj+1) I qi cu i I I .
Teorema 4. Pentru orice
algebra A exista un operator algebric de inchidere pe A ![]() A astfel incat
submultimile inchise ale lui A
A astfel incat
submultimile inchise ale lui A ![]() A sunt exact
congruentele lui A.
A sunt exact
congruentele lui A.
Demonstratie: Vom
organiza pe A ![]() A ca algebra astfel:
A ca algebra astfel:
In primul rand, pentru fiecare
operatie n - ara f de pe A consideram operatia n-ara g
de pe A ![]() A definita astfel :
A definita astfel :
g((a1, b1), , (an, bn)) = (f(a1, , an), f(b1, , bn)).
Daca la
operatiile astfel obtinute de pe A ![]() A mai adaugam operatia binara t
definita prin :
A mai adaugam operatia binara t
definita prin :
t((a, b),
(c, d)) = 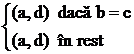
precum
si operatiile nule (a, a) pentru fiecare a I A, atunci se verifica ca q este subalgebra a lui A ![]() A daca si
numai daca q I Con
(A), astfel ca daca notam prin C operatorul Sg , avem ca Con (A) = (A
A daca si
numai daca q I Con
(A), astfel ca daca notam prin C operatorul Sg , avem ca Con (A) = (A ![]() A)C.
A)C.
Corolar 5. Pentru orice algebra A, Con (A) este latice algebrica. g
Definitia 6. Pentru o algebra A si a1, , an I A vom nota prin Q (a1, , an) relatia de congruenta de pe A generata de (adica cea mai mica congruenta de pe A, relativ la incluziune, astfel incat a1, a2, , an sunt in aceeasi clasa de echivalenta).
Congruenta Q (a1, a2) se zice congruenta principala.
Pentru o
multime Y A prin Q (Y) vom nota congruenta
generata de Y![]() Y.
Y.
Exemple.
. Daca G este un grup si a, b, c, d I G, atunci (a, b) I Q (c, d) daca si numai daca ab-1 este un produs finit de conjugati ai lui cd-1 si conjugati ai lui dc-1.
Daca A este un inel unitar si a, b,
c, d I A, atunci ( a, b ) I Q ( c, d ) daca si numai
daca a-b = ![]() ri (c-d) si cu ri, si
I A, 1 i n.
ri (c-d) si cu ri, si
I A, 1 i n.
Teorema 7. Fie A o algebra a1, b1, an, bn IA si q I Con A). Atunci:
i Q (a1, b1) = Q (b1, a1)
ii) Q ((a1, b1), , (an, bn)) = Q (a1, b1) ![]()
![]() Q (an, bn)
Q (an, bn)
iii) Q (a1, , an) = Q (a1, a2)![]() Q (a2, a3)
Q (a2, a3) ![]()
![]() Q (an-1, an)
Q (an-1, an)
iv) q ![]()
v) q
Demonstratie:
i) Cum (b1, a1 I Q (a1, b1) deducem ca Q (b1, a1) Q (a1, b1) si analog Q(a1, b1) Q(b1, a1), de unde egalitatea Q (a1, b1) = Q (b1, a1)
ii) Pentru 1 i n, (ai, bi) I Q ((a1, b1), ,(an, bn)) (caci Q ((a1, b1), , (an,bn)) este
relatia de congruenta de pe A generata de multimea deci Q (ai, bi) Q ((a1, b1), , (an, bn)), de unde
incluziunea Q (a1, b1) ![]()
![]()
![]() Q(an,bn) Q ((a1, b1), (an, bn)).
Q(an,bn) Q ((a1, b1), (an, bn)).
Pe de alta parte, pentru 1 i n, (ai, bi) I Q (ai, bi) Q ((a1, b1) ![]()
![]() Q(an, bn), astfel ca Q ((a1, b1)
Q(an, bn), astfel ca Q ((a1, b1) ![]()
![]() Q (an, bn), deci Q ((a1,b), (an, bn)) Q ((a1,
b1)
Q (an, bn), deci Q ((a1,b), (an, bn)) Q ((a1,
b1) ![]()
![]() Q (an, bn), de unde
egalitatea ceruta.
Q (an, bn), de unde
egalitatea ceruta.
iii) Pentru 1 i n-1 , (ai, ai+1) I Q (a1, , an), deci Q (ai ai+1) Q(a1,,an) astfel
ca Q (a1, a2) ![]()
![]() Q (an-1, an) Q (a1, , an).
Q (an-1, an) Q (a1, , an).
Invers, pentru 1 i < j n, (ai, aj) I Q (ai, ai+1) ![]()
![]() Q (aj-1, aj), adica (ai,aj)
I Q (ai , ai+1) Q (aj-1, aj), de unde
(ai, aj) I Q (a1, a2)
Q (aj-1, aj), adica (ai,aj)
I Q (ai , ai+1) Q (aj-1, aj), de unde
(ai, aj) I Q (a1, a2) ![]()
![]() Q (an-1, an).
Q (an-1, an).
In conformitate cu (i), Q (a1, , an) Q (a1, a2) ![]()
![]() Q (an-1, an), astfel
ca Q (a1, an) = Q(a1, a2)
Q (an-1, an), astfel
ca Q (a1, an) = Q(a1, a2) ![]()
![]() Q (an-1, an).
Q (an-1, an).
iv) Pentru (a, b) I q evident (a, b) I Q (a, b) q, astfel ca q ![]() q deci q
q deci q ![]()
v) Analog ca pentru iv).g
Fie A o algebra de tip t, de univers A si n I N *.
Definitia 8. Polinoamele n - are de tip t se definesc ca functii de la An in A astfel:
i)Proiectiile
pi,n : A n A, pi,n (a1, , an) = a![]() ( 1 i n ) sunt polinoame n - are.
( 1 i n ) sunt polinoame n - are.
ii)Daca p1, , pn![]() sunt polinoame n - are iar fi este
operatia algebrica ni - ara, atunci si functia fi (p1,
, pn
sunt polinoame n - are iar fi este
operatia algebrica ni - ara, atunci si functia fi (p1,
, pn![]() ) : An A, fi
(p1, , pn
) : An A, fi
(p1, , pn![]() ) (a1, , an) = fi
(p1 (a1, , an), , pn
) (a1, , an) = fi
(p1 (a1, , an), , pn![]() (a1, , an)) este polinom n -
ar.
(a1, , an)) este polinom n -
ar.
iii)Oricare alt polinom n - ar se obtine prin procedeele i) si ii) aplicate de un numar finit de ori.
Daca p : An A, (1 k n) este un polinom n - ar iar k variabile ale lui p au fost substituite cu anumite constante din A, obtinem astfel o functie de la An-k la A numita functie algebrica.
Exemple
. Daca ( L, ) este o latice, atunci singurul polinom unar a lui L este 1L
Iata exemple de polinoame binare: p : A2 A, p (x, y) = x, q : A2 A, q(x, y) = x y.
Daca (A, +, . , 0, 1) este un inel unitar, atunci orice polinom unar este de forma p (x) = n0 + n1x + + nmxm unde m I N iar ni este zero sau 1 + + 1 de un numar finit de ori.
. Daca (G, ) este un semigrup, atunci toate polinoamele unare ale lui G sunt de forma p (x) = xn (cu n I N).
Teorema 9. Fie A o algebra de univers A si H A o submultime nevida.
Atunci (c, d) I Q (H) daca si numai daca
exista nIN, un sir de elemente c = z0, z1,
, zn = d si perechile de elemente (ai, bi)
I H ![]() H si functiile
algebrice unare pi astfel incat pentru 1 i n.
H si functiile
algebrice unare pi astfel incat pentru 1 i n.
Demonstratie: Este suficient sa demonstram aceasta teorema doar in cazul H = , iar pentru aceasta sa notam prin r relatia de pe A definite prin conditiile din dreapta ale echivalentei din enunt.
Deoarece polinoamele au proprietatea de substituire, daca r I Con (A) si (a,b) I r, atunci pentru sirul (z1) n de elemente din A alese ca in enuntul teoremei avem ca I r, astfel ca (c, d) I r
Astfel, pentru a proba egalitatea Q (a, b) = r (tinand cont de faptul ca Q (a, b) este congruenta generata de (a, b)) este suficient sa probam ca rICon (A) si (a, b)Ir (atunci Q (a, b) r si cum r Q (a, b) vom avea egalitatea ceruta).
Faptul ca (a, b) I r este banal (putem alege sirul a, b si functia unara p (x)=x, x I A) ca si acela ca r I Echiv (A).
Ramane sa mai aratam ca r are proprietatea de substituire.
Fie deci fi
operatia ni - ara si (a0, b0),
,(an![]() , bn
, bn![]() ) I r (
1 i t
) I r (
1 i t
Conform definitiei lui r avem sirurile:
a0
= z![]() , , z
, , z![]() = b
= b![]()
a![]() = z
= z![]() , , z
, , z![]() = b
= b![]() de elemente din A si
de elemente din A si
p![]() , , p
, , p![]()
p![]() , , p
, , p![]() de functii algebrice unare de pe A ce verifica
conditiile impuse de definirea lui r
de functii algebrice unare de pe A ce verifica
conditiile impuse de definirea lui r
Vom proba prin inductie dupa i ca:
(fi (a0,
, an![]() -1), fi
(b0, , bn
-1), fi
(b0, , bn![]() -1)) I r
-1)) I r
Acest lucru este evident pentru i = 0; sa presupunem ca el este adevarat pentru i < ni.
Deoarece (ai, bi) I r, exista sirurile a1 = z0, , zm = b1 de elemente din A si p0, , pm-1 de polinoame unare de pe A astfel incat j m-1.
Considerand acum sirurile :
t0 = fi (b0,
, bi-1, z0, ai+1, , an![]() -1)
-1)
t1 = fi (b0,
, bi-1, z1, ai+1, ,an![]() -1)
-1)
tm = fi (bo,
, bi-1, zm, ai+1, , an![]() -1) de
elemente din A si
-1) de
elemente din A si
q0 = fi (b0, , bi-1, p0,
ai+1, , an![]()
q1 = fi (b0,
, bi-1, p1, ai+1, , an![]()
- - - - - - - - - - - - - - - - - - - - - - - - - -
qm-1 = fi (b0,
, bi-1, pm-1, ai+1, , an![]() -1) de functii algebrice unare ale lui A,
rezulta imediat (tinand cont de ipoteza de inductie) ca:
-1) de functii algebrice unare ale lui A,
rezulta imediat (tinand cont de ipoteza de inductie) ca:
(fi (b0,
, bi-1, ai, ai+1, , an![]() -1), fi (b0, , bi-1,
bi, ai+1, , an
-1), fi (b0, , bi-1,
bi, ai+1, , an![]() -1)) I r si prin tranzitivitatea lui r ca
-1)) I r si prin tranzitivitatea lui r ca
(fi(a0,
, an![]() -1), fi (b0, .. ,bn
-1), fi (b0, .. ,bn![]() -1)) I r, astfel ca r I Con
(A) si totul este probat.g
-1)) I r, astfel ca r I Con
(A) si totul este probat.g
Corolar 10. (c, d) I Q (a, b) daca si numai daca nIN*, un sir de elemente c = z0, , zn = b ale lui A si un sir de functii algebrice unare p0, p1, ,pn-1 astfel incat pentru 0 i n-1.
. Daca (G, ) este un grup si a, b, c, d I G, atunci (c, d) I Q (a, b) daca si numai daca exista un polinom unar p de pe G astfel incat p (a) = c si p (b) = d.
Daca A este un inel, cum o congruenta de pe A este si congruenta pe grupul aditiv (A, +), deducem ca pentru Q (a, b) pe inelul A avem aceeasi caracterizare ca in cazul grupurilor.
Definitia 11. O algebra A se zice congruent - modulara distributiva) daca (Con (A), ) este latice modulara (distributiva).
Vom spune despre A ca este congruent - permutabila daca oricare doua congruente ale lui A comuta.
Lema 1 Pentru o algebra A si q q I Con (A), urmatoarele afirmatii sunt echivalente :
i) q ![]() q q′
q q′![]() q
q
ii) q ![]() q q
q q ![]() q
q
iii) q ![]() q q′
q q′ ![]() q
q
Teorema 13. (Birkoff). Daca A este o algebra congruent - permutabila, atunci A este congruent - modulara.
Demonstratie:
Fie q q q I Con
(A) cu q q Pentru a demonstra legea de modularitate
este suficient sa probam incluziunea q q q q q q iar pentru aceasta fie (a, b) I q q q Conform lemei anterioare, q q q ![]() q deci exista c I A astfel incat (a, c) I q si (c, b) I q Atunci (c, a) I q q deci (c, a) I q si cum (a, b) I q deducem ca (c, b) I q adica (c, b) I q q
q deci exista c I A astfel incat (a, c) I q si (c, b) I q Atunci (c, a) I q q deci (c, a) I q si cum (a, b) I q deducem ca (c, b) I q adica (c, b) I q q
Din (a, c) I q si (c, b) I q q deducem ca (a, b) I q ![]() q q deci (a, b) I q q q de unde rezulta egalitatea din legea
de modularitate.g
q q deci (a, b) I q q q de unde rezulta egalitatea din legea
de modularitate.g
Fie A o algebra de tip t si q I Con (A).
Atunci A q devine algebra de tip t definim operatia ni - ara de pe A q prin:
fqi : (A q n![]() A q
A q
fqi (a1 q an q (fi (a1, , an)) q ( unde fi este operatia algebrica ni-ara a lui f, 1 i t)).
Corectitudinea definirii lui fqi ne este asigurata de faptul ca q I Con (A).
Aplicatia pq : A A q pq (a) = a q (a I A) este morfism surjectiv.
Vom prezenta cateva teoreme cunoscute in Algebra Universala sub numele de "teoremele de izomorfism " (folosim conventia ca atunci cand spunem ca o aplicatie f : A B este morfism de algebre vom subintelege ca A si B sunt algebre de acelasi tip t iar f este morfism de algebre de tip t
Vom nota pentru f I Hom (A, B) prin Im (f) imaginea lui A prin f, adica Im(f)= B.
Teorema 14. (Prima teorema de izomorfism). Fie A, B algebre si fIHom(A, B). Atunci A Ker (f) Im (f).
Demonstratie: Fie q Ker (f) I Con (A) si j : A Ker (f) Im (f), j (a q)= = f (a). Sa aratam ca j este izomorfismul cautat.
Intr-adevar, pentru a, b I A din echivalentele a q=b q (a, b)Iq f(a)=f(b) deducem ca j este corect definita si ca
functia este bijectie. Cum bijectivitatea lui j este imediata mai avem de probat
faptul ca j este morfism. Pentru aceasta fie fi o
operatie algebrica ni-ara de pe A (1 i t t fiind tipul lui A si B) si a1,
, an![]() IA.
IA.
Atunci fqi j (a1), , j (an)) = fqi (a1 q, ., an![]() q) = (fi (a1, ., an
q) = (fi (a1, ., an![]() )) q = =j(fqi (a1, ., an
)) q = =j(fqi (a1, ., an![]() )), adica j este morfism.g
)), adica j este morfism.g
Corolar 15. Daca f : A B este morfism surjectiv de algebre, atunci A Ker (f) B.
Fie A o algebra si f q I Con (A) cu q f
Daca notam f q I (A q (a, b) I f , se probeaza imediat ca f q I Con (A q
Teorema 16. (A doua teorema de izomorfism)
Daca f q I Con (A) si q f atunci (A q f q A f
Demonstratie: Definim j : A f A q prin j (a q) = a f (a I A).
Daca a, b I A si a f = b f, atunci (a, b) I q f, adica a f = b f, deci j este corect definita.
Daca fi este o
operatie ni - ara de pe A si a1, , an![]() I A (1 i t)), atunci j(fqi (a1 q), , (an
I A (1 i t)), atunci j(fqi (a1 q), , (an![]() q j ((fI (a1, .., an
q j ((fI (a1, .., an![]() )) q) = (fi (a1,., an
)) q) = (fi (a1,., an![]() )) f = (ffi (a1 f), ., (an
)) f = (ffi (a1 f), ., (an![]() f)) = ffi j (a1 q j (an
f)) = ffi j (a1 q j (an![]() q)), adica j este morfism (evident, surjectiv). Cum pentru
a, b I A avem (a q b q I Ker (j j (a q j (b q a f = b j (a, b) I f (a q b q I f q deducem ca Ker (j f q si totul rezulta acum din corolarul
anterior. g
q)), adica j este morfism (evident, surjectiv). Cum pentru
a, b I A avem (a q b q I Ker (j j (a q j (b q a f = b j (a, b) I f (a q b q I f q deducem ca Ker (j f q si totul rezulta acum din corolarul
anterior. g
Fie acum A o algebra, B A si q I Con (A).
Notam prin Bq subalgebra lui A generata de iar prin q B q B (daca B A atunci q B I Con (B)).
Teorema 17. (A treia teorema de izomorfism)
Daca B A si q I Con (A), atunci B q B Bq q Bq
Demonstratie: Se probeaza imediat ca izomorfismul cautat este aplicatia
j : B q B Bq q Bq j (b q B = b q Bq pentru orice b I B.g
Teorema 18. (Teorema de corespondenta)
Fie A o algebra si q I Con (A).
Atunci Con (A) q A] (ca latici).
Demonstratie: Vom proba ca a q A Con (A q a f f q f I q A]) este izomorfism de latici. Daca f I q A f ψ atunci putem spune ca exista a, b I A astfel incat (a, b) I f ψ (diferenta de multimi!). Atunci (a q, b q I f q q , adica a f a deci a este injectie.
Pentru ψ I Con (A q) daca vom considera f = Ker (pY pq ICon (A q , atunci (a q, b q I f q (a, b ) I f q, b q I f q ψ, adica a este si surjectie. Cum faptul ca a este morfism de latici, deducem ca a este izomorfism de latici.g
Observatie: Considerand cazul grupurilor sau inelelor, obtinem cunoscutele teoreme de izomorfism din algebra pentru grupuri si inele.
Definitia 19. Fie K o clasa de algebre de acelasi tip. Vom spune despre K ca are proprietatea de extindere a congruentei daca pentru orice A I K, orice B A si q I Con (B) exista f I Con (A) astfel incat f B q
Observatie: O
clasa ecuationala K
are proprietatea de extindere a congruentei daca si numai
daca pentru orice morfism injectiv f : A B si g : A C morfism surjectiv exista morfismul
surjectiv h : B D si morfismul injectiv k : C D astfel incat h ![]() f = k
f = k ![]() g:
g:
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |