Functii armonice
Exercitiul 1. Fie ![]() un interval al axei
reale si multimea
un interval al axei
reale si multimea ![]() care reprezinta
frontiera lui
care reprezinta
frontiera lui ![]() ; avem
; avem ![]() (adica,
(adica, ![]() ). Fie
). Fie ![]() , un camp scalar. Presupunem ca
, un camp scalar. Presupunem ca ![]() . Se cere:
. Se cere:
(i). Sa se arate ca multimea
functiilor ![]() armonice in
armonice in ![]() este nevida
(adica, in cazul unidimensional, functiile armonice verifica
ecuatia lui Laplace,
este nevida
(adica, in cazul unidimensional, functiile armonice verifica
ecuatia lui Laplace, ![]() ).
).
(ii). Aratati ca ![]() , unde
, unde ![]() sunt constante
arbitrare, reprezinta solutia generala a
ecuatiei lui Laplace. (Observam ca, in cazul unidimensional,
clasa functiilor armonice este "saraca",
aceasta se reduce la functiile lineare.
sunt constante
arbitrare, reprezinta solutia generala a
ecuatiei lui Laplace. (Observam ca, in cazul unidimensional,
clasa functiilor armonice este "saraca",
aceasta se reduce la functiile lineare.
(iii). Aratati ca daca
solutia ![]() atunci valorile lui
atunci valorile lui ![]() , in orice punct
, in orice punct ![]() , sunt unic determinate daca se cunosc valorile lui
, sunt unic determinate daca se cunosc valorile lui ![]() pe frontiera
domeniului
pe frontiera
domeniului ![]() , adica de numerele
, adica de numerele ![]() si
si ![]() . Scrieti expresia solutiei astfel determinate.
. Scrieti expresia solutiei astfel determinate.
(iv).
Presupunem ca solutia generala este de clasa ![]() pe
pe ![]() . Aratati ca daca se cunosc valorile
derivatelor lui
. Aratati ca daca se cunosc valorile
derivatelor lui ![]() dupa
directia normalei exterioare calculate pe frontiera lui
dupa
directia normalei exterioare calculate pe frontiera lui ![]() atunci solutia
atunci solutia ![]() este determina in
orice punct
este determina in
orice punct ![]() , eventual, abstractie facand de o constanta
reala.
, eventual, abstractie facand de o constanta
reala.
(derivata functiei ![]() dupa
directia normalei exterioare pe frontiera lui
dupa
directia normalei exterioare pe frontiera lui ![]() este definita de
una din expresiile:v
este definita de
una din expresiile:v 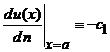 sau
sau 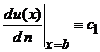 ).
).
(v). Sa se arate ca daca
functia ![]() , este armonica in domeniul
, este armonica in domeniul ![]() si
si ![]() , atunci valorile maxime si minime (extremele absolute)
ale lui
, atunci valorile maxime si minime (extremele absolute)
ale lui ![]() sunt atinse in
capetele intervalului de definitie (adica, pe frontiera
sunt atinse in
capetele intervalului de definitie (adica, pe frontiera ![]() domeniului de
definitie). Deci, pentru orice
domeniului de
definitie). Deci, pentru orice ![]() , avem
, avem
![]() .
.
(vi). Fie ![]() un punct oarecare, dar
fixat si
un punct oarecare, dar
fixat si ![]() o vecinatate
centrata in
o vecinatate
centrata in ![]() si evident,
continuta in intervalul
si evident,
continuta in intervalul ![]() . Aratati ca valoarea solutiei in punctul
. Aratati ca valoarea solutiei in punctul
![]() este egala cu
media valoarilor sale pe frontiera
este egala cu
media valoarilor sale pe frontiera ![]() . Calculati valoarea medie a functiei armonice
. Calculati valoarea medie a functiei armonice ![]() pe intervalul
pe intervalul ![]() .
.
De aici, deducem urmatoarele
Consecinta 1. Valoarea medie a unei
functii armonice ![]() este aceeasi pe
orice doua intervale centrate in acelasi punct
este aceeasi pe
orice doua intervale centrate in acelasi punct ![]() (continute in
(continute in ![]() ).
).
Consecinta 2. O functie
armonica definita in interiorul unei sfere ![]() , centrate in
, centrate in ![]() , de raza
, de raza ![]() , care este egala cu o constanta in toate punctele
frontierei
, care este egala cu o constanta in toate punctele
frontierei ![]() , se reduce la o constanta in orice punct din interiorul
sferei
, se reduce la o constanta in orice punct din interiorul
sferei ![]() .
.
(Expresia, 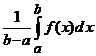 , defineste valoarea medie a functiei (integrabile)
, defineste valoarea medie a functiei (integrabile)
![]() pe intervalul
pe intervalul ![]() ).
).
Exercitiul 2. Fie ![]() un domeniu
bidimensional. Campul scalar
un domeniu
bidimensional. Campul scalar ![]() este armonic in
este armonic in ![]()
![]() functia
functia ![]() verifica, in
domeniul D, ecuatia
lui Laplace
verifica, in
domeniul D, ecuatia
lui Laplace
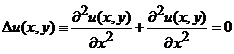 ,
, ![]() . (1)
. (1)
(i). Aratati ca multimea
functiilor armonice definite pe ![]() este nevida (!).
este nevida (!).
(ii). Sa se arate
ca functia 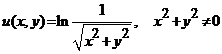 este armonica in
este armonica in ![]() .
.
Exercitiul 3. Fie domeniul bidimensional ![]() si campul scalar
si campul scalar ![]() . Atunci, definim operatorul lui Laplace,
. Atunci, definim operatorul lui Laplace,
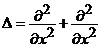 . (2)
. (2)
(a).
Fie transformarea de coordonate
polare: ![]() ,
, ![]() . Aratati ca:
. Aratati ca:
(i). operatorul lui Laplace (in coordonate polare) are forma
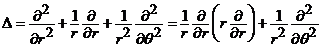 . (3)
. (3)
(ii).
functia compusa ![]() verifica
relatia
verifica
relatia
![]() sau, sub forma
sau, sub forma ![]() . (4)
. (4)
(b). Fie transformarea de coordonate cilindrice:
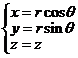 ,
, ![]() .
.
Aratati ca:
(i). Operatorul lui Laplace (in coordonate cilindrice) are forma
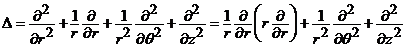 . (5)
. (5)
(ii).
Functia compusa ![]() verifica
relatia
verifica
relatia
![]() sau
sau ![]() . (6)
. (6)
(iii).
Daca functia ![]() depinde numai de
distanta
depinde numai de
distanta ![]() , de la axa de simetrie
, de la axa de simetrie ![]() a cilindrului
pana la un punct oarecare
a cilindrului
pana la un punct oarecare ![]() al cilindrului,
adica
al cilindrului,
adica ![]() , unde
, unde ![]() (adica, functia
(adica, functia
![]() nu depinde de
variabilele independente
nu depinde de
variabilele independente ![]() si
si ![]() ), atunci spunem ca functia
), atunci spunem ca functia ![]() este cu simetrie cilindrica si expresia
(6), a laplacianului, devine
este cu simetrie cilindrica si expresia
(6), a laplacianului, devine
![]() . (7)
. (7)
(iv).
Presupunem ca functia ![]() este cu simetrie cilindrica
este cu simetrie cilindrica ![]() . Se cere sa se determine solutia generala a
ecutiei
. Se cere sa se determine solutia generala a
ecutiei ![]() .
.
Indicatie.
Din (7) rezulta ca functia compusa ![]() verifica
ecuatia
verifica
ecuatia ![]() , care, prin integrarea in raport cu
, care, prin integrarea in raport cu ![]() , conduce la ecuatia diferentiala
, conduce la ecuatia diferentiala ![]() . Apoi, integrand, inca odata, obtinem solutia
. Apoi, integrand, inca odata, obtinem solutia
![]() , care depinde de doua constante arbitrare
, care depinde de doua constante arbitrare ![]() .
.
(c). Fie transformarea de coordonate sferice:
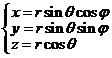 ,
, ![]() .
.
Sa se arate ca:
(i). Operatorul lui Laplace are forma
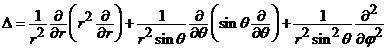 . (8)
. (8)
(ii).
Functia compusa ![]() , presupusa de clasa
, presupusa de clasa ![]() verifica
relatia
verifica
relatia
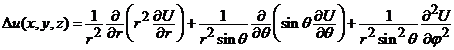 . (9)
. (9)
(iii).
Daca functia ![]() depinde numai de
distanta
depinde numai de
distanta ![]() , de la origine pana la un punct
, de la origine pana la un punct ![]() oarecare din
spatiu, adica
oarecare din
spatiu, adica ![]() , unde
, unde ![]() , atunci spunem ca functia
, atunci spunem ca functia ![]() este cu simetrie sferica si expresia (9),
a laplacianului lui
este cu simetrie sferica si expresia (9),
a laplacianului lui ![]() , devine
, devine
![]() . (10)
. (10)
Fie ![]() , un domeniu,
, un domeniu, ![]() si
si ![]() (distanta de la
origine pana la un punct oarecare
(distanta de la
origine pana la un punct oarecare ![]() din spatiu).
din spatiu).
(i).
Daca ![]() este o functie cu
simetrie sferica si
functia compusa
este o functie cu
simetrie sferica si
functia compusa ![]() , atunci
, atunci
![]()
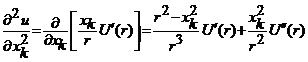 ,
, ![]()
si expresia laplacianului are forma:
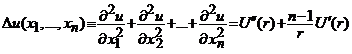 , in
, in ![]() .
.
(ii).
Daca ![]() atunci functia
atunci functia 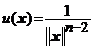 este armonica in
domeniul
este armonica in
domeniul ![]() .
.
Corespunzator, functia ![]() verifica
ecuatia lui Laplace
verifica
ecuatia lui Laplace ![]() in domeniul spatial
in domeniul spatial
![]() .
.
Se considera campul scalar al distantelor de la origine la
punctul ![]() din spatiu,
definit prin
din spatiu,
definit prin
![]() ,
, ![]() , unde
, unde ![]() .
.
Fie ![]() vectorul de
pozitie al punctului
vectorul de
pozitie al punctului ![]() si vectorii
si vectorii ![]() ,
, ![]() , fixati.
Notam cu
, fixati.
Notam cu ![]() , produsul scalar
al vectorilor
, produsul scalar
al vectorilor ![]() si
si ![]() si prin
si prin ![]() , produsul vectorial
al acestor vectori.
, produsul vectorial
al acestor vectori.
Aratati ca au loc relatiile:
(1). ![]() ;
;
(2). ![]() ;
;
(3). ![]() ;
;
(4). ![]()
(5). ![]() si
si ![]() .
.
(6). ![]() si
si ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |