PARTEA a II -a
I. Vectori in plan
Marimile intalnite in fizica, geometrie si alte stiinte sunt de mai multe feluri din care importante sunt doua: marimi scalare si marimi vectoriale.
Definitie. O marime este scalara, daca pentru determinarea ei este suficient sa indicam un singur numar.
Exemple: lungimea unui segment, masura unui unghi, aria unei suprafete, temperatura, etc.
Definitie. O marime se numeste vectoriala, daca ea este caracterizata de trei elemente: lungime (modul), directie si sens.
Exemple: viteza unui mobil, forta, campul electric, etc.
In cele ce urmeaza vom nota cu P multimea punctelor unui plan.
Fie d o
dreapta din plan (d![]() P).
P).
 Definitie Numim directie a dreptei d
multimea formata din dreapta d si toate dreptele paralele cu d.
Definitie Numim directie a dreptei d
multimea formata din dreapta d si toate dreptele paralele cu d.




 d
d
Prin urmare doua drepte d1 si d2 au
aceeasi directie daca sunt paralele
sau coincid. d
![]()

![]() Fie dreapta d pe care am fixat doua B
Fie dreapta d pe care am fixat doua B
puncte A, B (A![]() B). Punctele dreptei A
B). Punctele dreptei A
d pot fi parcurse de la A spre B (un sens
de parcurgere) sau de la B spre A (un alt sens de parcurgere, opus primului).
In acest mod spunem ca pe dreapta d am definit doua sensuri.
1.1 Segment orientat (vector legat)
Definitie ![]() O pereche ordonata (A,B), A, B
O pereche ordonata (A,B), A, B![]() P se numeste segment orientat sau
vector legat in A si se noteaza
P se numeste segment orientat sau
vector legat in A si se noteaza ![]() Punctul A se
numeste originea, iar punctul B se numeste extremitatea segmentului orientat.
Punctul A se
numeste originea, iar punctul B se numeste extremitatea segmentului orientat.
![]()
![]() B
B
A
Vectorul legat ![]() se numeste vectorul
legat nul si are dreapta suport nedeterminata.
se numeste vectorul
legat nul si are dreapta suport nedeterminata.
![]()
![]() A B
A B
![]() C D
C D
Vectorii ![]() si
si ![]() au sensuri opuse (sunt orientati diferit) daca au aceeasi
directie, si extremitatile lor B,D se afla in semiplane diferite
determinate de dreapta AC.
au sensuri opuse (sunt orientati diferit) daca au aceeasi
directie, si extremitatile lor B,D se afla in semiplane diferite
determinate de dreapta AC.
![]() A B
A B
D C
Definitie
Se
numeste modulul (lungimea, norma) vectorului
![]() , lungimea segmentului [AB].
, lungimea segmentului [AB].
Notatie: Modulul vectorului ![]() se noteaza prin |
se noteaza prin |![]() | sau ||
| sau ||![]() || sau simplu AB.
Pentru vectorul nul
|| sau simplu AB.
Pentru vectorul nul ![]()
![]()
Definitie Se numeste versor sau vector unitate vectorul avand modulul egal cu 1.
Definitie Numim vector liber multimea tuturor vectorilor legati care: au aceeasi directie,acelasi sens si acelasi modul.
![]()
![]() Notatie Vectorii liberi se
noteaza cu bara deasupra a, b,.
Notatie Vectorii liberi se
noteaza cu bara deasupra a, b,.
![]() Prin urmare daca
Prin urmare daca ![]() este un vector legat, atunci
este un vector legat, atunci ![]() , reprezinta multimea tuturor vectorilor
legati care au aceeasi directie, acelasi sens, acelasi
modul cu vectorul
, reprezinta multimea tuturor vectorilor
legati care au aceeasi directie, acelasi sens, acelasi
modul cu vectorul ![]() .
.
![]()
![]() B
B

A
![]()
![]()
Multimea vectorilor liberi din planul P o notam v.
Spunem ca
vectorul legat ![]()
![]() este un reprezentant al vectorului liber
este un reprezentant al vectorului liber ![]() si scriem
si scriem ![]() I
I![]() .
.
1.2. Relatia de echipolenta pe multimea vectorilor legati.
Definitie Doi vectori legati ![]() ,
,![]() I
I![]() se numesc vectori echipolenti
(adica vectorii
se numesc vectori echipolenti
(adica vectorii ![]() ,
,![]() au aceeasi directie, acelasi sens,
acelasi modul).
au aceeasi directie, acelasi sens,
acelasi modul).
Scriem acest lucru
astfel ![]()
![]() (citim vectorul
(citim vectorul ![]() este echipolent cu
vectorul
este echipolent cu
vectorul ![]() ).
).
i) ![]()
![]() (
(![]() ,
,![]() au aceeasi directie intrucat ABCD este
paralelogram, acelasi sens, acelasi modul;
au aceeasi directie intrucat ABCD este
paralelogram, acelasi sens, acelasi modul;
ii) Segmentele [AD] si [BC] au acelasi mijloc.
Observatie Daca in aplicatii intervin vectori liberi, vom lucra cu reprezentanti ai acestora, ceea ce permite sa luam originile acestor reprezentanti oriunde in plan.
1.3. Vectori colineari
Definitie Doi vectori liberi nenuli se numesc colineari daca au aceeasi directie. Se admite ca vectorul nul este coliniar cu orice vector.
1.4. Egalitatea a doi vectori liberi
Definitie Doi vectori liberi sunt egali daca au aceeasi directie, acelasi sens si acelasi modul.
Definitie Numim vectori opusi, doi vectori cu aceeasi directie, acelasi modul si sensuri opuse.
Avem de exemplu ![]() = --
= -- ![]()



 Regula
paralelogramului A C
Regula
paralelogramului A C ![]() O B
O B
![]()
Fig.1
Consideram ![]() I
I![]() ,
,![]() I
I![]() . Construim paralelogramul OBCA.
Vectorul
. Construim paralelogramul OBCA.
Vectorul ![]() de reprezentant
de reprezentant ![]() , reprezinta suma vectorilor
, reprezinta suma vectorilor ![]() si
si ![]() ;
; ![]() =
=![]() +
+![]() ; Se arata usor ca in definitia sumei
nu are importanta alegerea reprezentantilor
; Se arata usor ca in definitia sumei
nu are importanta alegerea reprezentantilor ![]() ,
,![]() pentru
pentru ![]() respectiv
respectiv ![]() (Fig.1).
(Fig.1).
2) Regula triunghiului
![]()
![]()
![]()
![]() A B
A B
![]()
![]()
![]()
![]()
![]() Fig.2
Fig.2
O
Aceasta regula de adunare a vectorilor se numeste regula triunghiului.
Observatie Daca ![]() +
+![]() +
+![]() =0, atunci cu vectorii
=0, atunci cu vectorii ![]() ,
,![]() ,
,![]() se poate forma un triunghi.
se poate forma un triunghi.
3) Regula poligonului
Vectorul ![]() care inchide conturul
(uneste originea primului vector cu extremitatea ultimului vector
reprezinta suma vectorilor date:
care inchide conturul
(uneste originea primului vector cu extremitatea ultimului vector
reprezinta suma vectorilor date: ![]() =
=![]() +
+![]() +
+![]() (Fig.3)
(Fig.3)



![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Fig.3
2.2. Proprietatile adunarii vectorilor liberi
Adunarea vectorilor liberi este asociativa:
(![]() +
+![]() ) +
) + ![]() =
= ![]() + (
+ (![]() +
+![]() ) , (
) , (![]() )
) ![]() ,
, ![]() ,
, ![]() I V
I V
Demonstratia este realizata in Fig.4 (s-a folosit pentru adunare regula triunghiului).
![]()
![]()

![]()
![]() +
+![]()
![]() +
+![]()
![]()
(![]() +
+![]() ) +
) + ![]() =
= ![]() + (
+ (![]() +
+![]() )
)
Fig.4
2) Adunarea vectorilor liberi
este comutativa: ![]()
![]()
![]()
![]()
![]() +
+![]() =
=![]() +
+![]() , (
, (![]() )
)![]() ,
, ![]() I V
I V
Demonstratia este realizata in Fig.5.
![]()
![]() +
+![]() =
=![]() +
+![]()
![]()
![]()
![]()
Vectorul nul ![]() este elementul neutru pentru
adunarea vectorilor liberi:
este elementul neutru pentru
adunarea vectorilor liberi: ![]() +
+![]() =
=![]() +
+![]() =
=![]() , (
, (![]() )
) ![]() I V
I V
Pentru orice vector ![]() I V, exista vectorul (-
I V, exista vectorul (-![]() )IV astfel incat
)IV astfel incat
![]() +(-
+(-![]() )=(-
)=(-![]() )+
)+![]() =
=![]()
-![]() se numeste opusul lui
se numeste opusul lui ![]()
2.3. Inmultirea unui vector liber cu un scalar
Definitie Fie rI R*, ![]() I v,
I v, ![]()
![]() . Produsul dintre numarul real r
si vectorul liber
. Produsul dintre numarul real r
si vectorul liber ![]() este vectorul notat r
este vectorul notat r![]() , care:
, care:
i)
are aceeasi directie cu ![]()
ii)
 daca r >0 are acelasi sens cu
daca r >0 are acelasi sens cu ![]()
 daca r <0 are sens contrar cu
daca r <0 are sens contrar cu ![]()
iii)
![]() are modulul egal cu produsul dintre |r| si |
are modulul egal cu produsul dintre |r| si |![]() | :
| :
 |r
|r ![]() |=|r| |
|=|r| |![]() |
|
![]() Daca r = 0 sau
Daca r = 0 sau
![]() =
= ![]() , atunci r
, atunci r![]() =
=![]()
 -3
-3![]()
![]()
 Exemplu 2
Exemplu 2 In Fig.6 sunt reprezentati vectorii
In Fig.6 sunt reprezentati vectorii

Fig.6
2.4. Proprietati ale inmultirii unui vector cu un scalar
1) r (![]() +
+![]() ) = r
) = r![]() +r
+r![]() , (
, (![]() ) r I R,
(
) r I R,
(![]() )
)![]() ,
,![]() Iv
Iv
(Inmultirea cu scalari este distributiva fata de adunarea vectorilor)
2) (r + s)
![]() = r
= r![]() + s
+ s ![]() , (
, (![]() ) r, s I R,
(
) r, s I R,
(![]() )
)![]() Iv
Iv
(Inmultirea cu scalari este distributiva fata de adunarea scalarilor)
3) r (s![]() ) = (rs)
) = (rs) ![]() , (
, (![]() ) r, s I R,
(
) r, s I R,
(![]() )
)![]() Iv
Iv
(Asociativitatea scalarilor)
4) 1![]() =
= ![]() , (
, (![]() )
)![]() Iv
Iv
(Numarul 1 este element neutru pentru inmultirea cu scalari)
Demonstrarea acestor proprietati se face in mod similar cu demonstrarea proprietatilor de la adunarea vectorilor liberi.
2.5.Vectori colineari
Definitie Doi vectori liberi nenuli se numesc colineari atunci cand au aceeasi directie. In caz contrar vectorii se numesc necolineari. Admitem ca vectorul nul este coliniar cu orice vector.
Din definitie, rezulta ca doi vectori sunt colineari atunci cand au aceeasi dreapta suport sau drepte suport paralele.
Vectorilor necolineari le corespund drepte suport concurente.
In Fig.7 (a,b,c,d) sunt reprezentati vectori colineari.

![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
a) b) c) d)
Fig.7
Vom caracteriza conditia de coliniaritate a doi vectori enuntand urmatoarea teorema:
Cazul 2: Vectorii ![]() ,
, ![]() au sensuri opuse. In
acest caz luam r = -
au sensuri opuse. In
acest caz luam r = -![]() si observam ca
si observam ca ![]() = r
= r![]() (vectorii din cei doi membri au aceeasi directie, acelasi
sens (r <0) si acelasi modul).
(vectorii din cei doi membri au aceeasi directie, acelasi
sens (r <0) si acelasi modul).
Reciproc presupunem ca ![]() = r
= r![]()
Intrucat vectorii ![]() si r
si r![]() au aceeasi directie, cum
au aceeasi directie, cum ![]() = r
= r![]() , rezulta ca
, rezulta ca ![]() si
si ![]() au aceeasi directie,
deci sunt colineari.
au aceeasi directie,
deci sunt colineari.
Observatii
1) Colinearitatea a trei puncte
Fie A, B, C trei puncte. Ele sunt colineare
(situate pe aceeasi dreapta) daca si numai daca ![]() ,
, ![]() sunt vectori
colineari, deci daca si numai daca, exista r I R astfel incat
sunt vectori
colineari, deci daca si numai daca, exista r I R astfel incat ![]() = r
= r![]() .
.
2) Paralelismul a doua drepte
Vectorii ![]() si
si ![]() sunt colineari daca si
numai daca dreptele AB, CD sunt paralele sau coincid.
sunt colineari daca si
numai daca dreptele AB, CD sunt paralele sau coincid.
3) ![]() ,
,![]() I v (vectori liberi nenuli) sunt colineari, daca
si numai daca exista r, s
I R nenule simultan astfel incat r
I v (vectori liberi nenuli) sunt colineari, daca
si numai daca exista r, s
I R nenule simultan astfel incat r![]() + s
+ s![]() =
= ![]()
Rezulta de aici ca daca ![]() ,
,![]() I v sunt necolineari atunci r
I v sunt necolineari atunci r![]() + s
+ s![]() =
= ![]() daca si numai
daca r = s = 0.
daca si numai
daca r = s = 0.
In cele ce urmeaza vom pune in evidenta o relatie vectoriala extrem de importanta, relatie ce va permite exprimarea vectorilor importanti intr-un triunghi. Enuntam aceasta proprietate sub forma de:
Teorema
2 Fie A, B
doua puncte diferite din plan si M I [AB],
astfel incat ![]() = k , (
= k , (![]() = k
= k![]() ), iar O un punct arbitrar al planului (Fig.8).
), iar O un punct arbitrar al planului (Fig.8).
Atunci ![]() =
= ![]()
![]() +
+ ![]()
![]()

![]()
 O
O
![]() A M B
A M B
Fig.8
Demonstratie Aplicand de doua ori regula triunghiului, obtinem egalitatile
vectoriale ![]() =
= ![]() +
+ ![]() ;
; ![]() =
= ![]() +
+ ![]()
Conform ipotezei, putem scrie ![]() +
+ ![]() = k (
= k (![]() +
+ ![]() ) sau
) sau ![]() - k
- k ![]() = -
= -![]() + k
+ k ![]() , sau
, sau ![]() + k
+ k ![]() =
= ![]() + k
+ k ![]() , sau
, sau
(1 + k ) ![]() =
= ![]() + k
+ k ![]() de unde rezulta :
de unde rezulta :
![]() =
= ![]()
![]() +
+ ![]()
![]()
2.6. Probleme rezolvate
Fie ABC un triunghi si G centrul sau de greutate. Sa se arate ca:
a) ![]() +
+ ![]() +
+ ![]() =
= ![]()
b) Pentru orice
punct M din planul triunghiului: ![]() +
+![]() +
+![]() = 3
= 3![]()
![]()
![]()

 a) Fie A` mijlocul lui [BC].
a) Fie A` mijlocul lui [BC].
Avem ![]() =
= ![]() (
( ![]() +
+![]() ) iar
) iar
![]() =
= ![]()
![]() G
G
![]() = -
= -![]()
![]() = -
= -![]() (
( ![]() +
+![]() ) B A` C
) B A` C
Analog ![]() = -
= -![]() (
( ![]() +
+![]() ) si
) si ![]() = -
= -![]() (
( ![]() +
+![]() )
)
Rezulta ![]() +
+ ![]() +
+![]() = -
= -![]() (
(![]() +
+ ![]() +
+ ![]() ) =
) =
= -![]() (
(![]() +
+ ![]() ) = -
) = -![]()
![]() =
= ![]()
b) Fie M un punct oarecare din planul triunghiului
![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
=
= 3 ![]() + (
+ (![]() +
+ ![]() +
+ ![]() ) = 3
) = 3 ![]() (s-a tinut cont de
punctul a).
(s-a tinut cont de
punctul a).
Observatie Se poate constata usor ca cele doua egalitati vectoriale de la a) si b) sunt echivalente.
Fie ABC un triunghi de laturi a, b, c si I centrul cercului inscris. Sa se arate ca:
a) a ![]() + b
+ b ![]() + c
+ c ![]() =
= ![]() ;
;
b) Pentru orice punct M din planul
triunghiului: a![]() +b
+b![]() +c
+c![]() = =(a+b+c)
= =(a+b+c)![]()
Solutie A
![]()
![]() a) Fie AA`, BB` bisectoarele unghiurilor A si B, b
a) Fie AA`, BB` bisectoarele unghiurilor A si B, b
iar I punctul lor de intersectie. Aplicand teorema B`
 bisectoarei in triunghiul ABB`, obtinem
bisectoarei in triunghiul ABB`, obtinem ![]() =
=![]() c I
c I
![]() si aplicand teorema bisectoarei in triunghiul ABC B C
si aplicand teorema bisectoarei in triunghiul ABC B C
obtinem
![]() =
=![]() sau
sau ![]() =
=![]() . Rezulta AB`=
. Rezulta AB`=![]() A` a
A` a
Prin urmare ![]() =
=![]() . Conform teoremei 2, rezulta
. Conform teoremei 2, rezulta
![]() =
=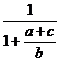
![]() +
+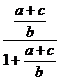
![]() sau
sau ![]() =
=![]()
![]() +
+![]()
![]()
Dar ![]() =
=![]()
![]() , deci
, deci ![]() =
=![]()
![]() +
+![]()
![]()
Rezulta
![]() =
=![]()
![]() +
+![]()
![]() Analog
Analog
![]() =
=![]()
![]() +
+![]()
![]()
![]() =
=![]()
![]() +
+![]()
![]()
Atunci a![]() + b
+ b![]() + c
+ c![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() =
= ![]() (
(![]() +
+ ![]() ) +
) + ![]() (
(![]() +
+ ![]() ) +
) + ![]() (
(![]() +
+ ![]() ) =
) = ![]()
b) Daca M este un punct oarecare din planul triunghiului ABC, putem scrie sirul de egalitati:
a![]() + b
+ b![]() + c
+ c![]() = a(
= a(![]() +
+ ![]() ) + b(
) + b(![]() +
+ ![]() ) + c(
) + c(![]() +
+![]() ) = = (a+b+c)
) = = (a+b+c) ![]() + a
+ a![]() + b
+ b![]() + c
+ c![]() = (a+b+c)
= (a+b+c) ![]() (s-a tinut cont de
punctul a)
(s-a tinut cont de
punctul a)
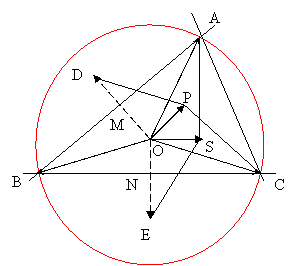 Fie triunghiul oarecare ABC iar H
ortocentrul sau. Demonstrati ca:
Fie triunghiul oarecare ABC iar H
ortocentrul sau. Demonstrati ca:
a) ![]() +
+ ![]() +
+ ![]() =
= ![]() (Relatia
lui Sylvester)
(Relatia
lui Sylvester)
b) ![]() +
+ ![]() +
+ ![]() = 2
= 2![]()
Solutie
a) Exprimam ![]() +
+ ![]() +
+ ![]() in doua moduri:
in doua moduri:
i)(![]() +
+ ![]() ) +
) + ![]() si
si
ii)![]() + (
+ (![]() +
+ ![]() ).
).
Evident ca cele doua exprimari sunt egale datorita
proprietatii de asociativitate a adunarii vectorilor.
Fie M mijlocul segmentului [AB].
(![]() +
+ ![]() ) =
) = ![]() , unde D este simetricul lui O fata de M si OD
, unde D este simetricul lui O fata de M si OD ![]() AB.
AB.
(![]() +
+ ![]() ) +
) + ![]() =
= ![]() +
+ ![]() =
= ![]() , unde P este al patrulea varf al paralelogramului ODPC
construit pe laturile OC si OD.
, unde P este al patrulea varf al paralelogramului ODPC
construit pe laturile OC si OD.
Retinem deci ca
i) (![]() +
+![]() )+
)+ ![]() =
=![]() , unde CP || OD deci CP
, unde CP || OD deci CP ![]() AB, deci P se afla pe inaltimea din C a triunghiului ABC.
AB, deci P se afla pe inaltimea din C a triunghiului ABC.
Fie N mijlocul
segmentului [BC]. ![]() +
+ ![]() =
= ![]() , unde E este simetricul lui O fata de N si ON
, unde E este simetricul lui O fata de N si ON ![]() BC.
BC.
![]() + (
+ (![]() +
+ ![]() ) =
) = ![]() +
+ ![]() =
= ![]() , unde S este al patrulea varf al paralelogramului OASE
construit pe laturile OA si OE.
, unde S este al patrulea varf al paralelogramului OASE
construit pe laturile OA si OE.
Retinem deci
ca ii)![]() +(
+(![]() +
+![]() )=
)=![]() , unde AS||ON, deci AS
, unde AS||ON, deci AS ![]() BC, deci S se afla pe
inaltimea din A a triunghiului ABC.
BC, deci S se afla pe
inaltimea din A a triunghiului ABC.
Din i) si ii)
rezulta ![]() =
= ![]() , deci punctele P si S coincid. Cum unul se afla pe inaltimea
din C, iar celalalt pe inaltimea din A, rezulta ca
, deci punctele P si S coincid. Cum unul se afla pe inaltimea
din C, iar celalalt pe inaltimea din A, rezulta ca ![]() +
+ ![]() +
+ ![]() este un vector de
origine O si de extremitate punctul de intersectie a doua inaltimi ale
triunghiului (ortocentrul triunghiului). Asadar am demonstrat ca
este un vector de
origine O si de extremitate punctul de intersectie a doua inaltimi ale
triunghiului (ortocentrul triunghiului). Asadar am demonstrat ca ![]() +
+ ![]() +
+ ![]() =
= ![]() .
.
b) ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() +
+ ![]() = 3
= 3![]() -
- ![]() = 2
= 2![]() .
.
Sa se arate ca in orice triunghi ABC, punctele O, G, H sunt colineare (dreapta care le uneste se numeste dreapta lui Euler).
Solutie
Conform
problemei rezolvate nr.1, putem scrie ca ![]() =
= ![]() (
(![]() +
+ ![]() +
+ ![]() ), iar conform problemei rezolvate nr.3,
), iar conform problemei rezolvate nr.3, ![]() =
= ![]() +
+ ![]() +
+ ![]() ).
).
Din cele doua
egalitati vectoriale deducem ca ![]() =
= ![]()
![]() , deci ca vectorii
, deci ca vectorii ![]() si
si ![]() sunt colineari, si cum au originea comuna, rezulta ca
punctele O, G, H sunt colineare.
sunt colineari, si cum au originea comuna, rezulta ca
punctele O, G, H sunt colineare.
Sa se demonstreze ca in orice trapez, dreapta care uneste mijloacele diagonalelor este paralela cu bazele trapezului.
Solutie
![]()
![]()
![]()
 Fie M, N mijloacele diagonalelor AC, D C
Fie M, N mijloacele diagonalelor AC, D C
respectiv BD. vom arata ca vectorii
![]() si
si ![]() sunt colineari. M N
sunt colineari. M N
A B
![]() =
= ![]() -
- ![]() =
= ![]() (
(![]() +
+ ![]() ) -
) - ![]()
![]() =
= ![]() (
(![]() +
+ ![]() ) -
) - ![]() (
(![]() +
+ ![]() ) =
) = ![]() (
(![]() -
- ![]() ). Dar vectorii
). Dar vectorii ![]() si
si ![]() sunt colineari, prin
urmare, exista r I R
a.i.
sunt colineari, prin
urmare, exista r I R
a.i. ![]() = r
= r![]() , asa incat
, asa incat ![]() =
= ![]() (
(![]() - r
- r![]() ) =
) = ![]()
![]() , deci vectorii
, deci vectorii ![]() si
si ![]() sunt colineari, adica
MN || AB || CD.
sunt colineari, adica
MN || AB || CD.
Sa se arate ca in orice trapez, mijloacele bazelor, punctul de intersectie al diagonalelor si punctul de intersectie al laturilor neparalele sunt patru puncte colineare.
Solutie
![]()
![]()

![]()
 a) Aratam pentru inceput ca punctele O, H, E sunt colineare.
a) Aratam pentru inceput ca punctele O, H, E sunt colineare.
![]() =
= ![]() (
(![]() +
+ ![]() ) O
) O
![]() =
= ![]() (
(![]() +
+ ![]() )
)
Din DC || AB T ![]() =
= ![]()
![]() k T D H C
k T D H C
T OD = k OA si OC = kOB deci F
![]() = k
= k![]() si
si ![]() = k
= k![]()
Atunci ![]() =
= ![]() (k
(k![]() + k
+ k![]() ) = A
E B
) = A
E B
![]() (
(![]() +
+ ![]() ) = k
) = k![]() ceea ce exprima faptul ca vectorii
ceea ce exprima faptul ca vectorii ![]() ,
, ![]() sunt colineari si cum
au originea comuna rezulta ca punctele O, H, E sunt colineare.
sunt colineari si cum
au originea comuna rezulta ca punctele O, H, E sunt colineare.
b) Aratam acum
ca punctele O, H, F sunt colineare (vectorii ![]() si
si ![]() sunt colineari)
sunt colineari)
![]() =
= ![]() (
(![]() +
+ ![]() ). Am vazut la a) ca
). Am vazut la a) ca ![]() =
= ![]() = k, deci si
= k, deci si ![]() = k si cum
triunghiurile DFC si AFB sunt asemenea, rezulta ca
= k si cum
triunghiurile DFC si AFB sunt asemenea, rezulta ca ![]() = k. In aceste
conditii
= k. In aceste
conditii ![]() =
= ![]()
![]() +
+ ![]()
![]() si intrucat
si intrucat ![]() = k
rezulta: OB =
= k
rezulta: OB = ![]() OC, deci
OC, deci ![]() =
=![]()
![]() . Atunci
. Atunci ![]() =
= ![]()
![]() +
+ ![]()
![]()
![]() =
= ![]() (
(![]() +
+![]() ) =
) = ![]()
![]() , deci
, deci ![]() =
= ![]()
![]() ceea ce probeaza
faptul ca vectorii
ceea ce probeaza
faptul ca vectorii ![]() si
si ![]() sunt colineari si cum
au aceeasi origine rezulta ca punctele O, F, H sunt colineare.
sunt colineari si cum
au aceeasi origine rezulta ca punctele O, F, H sunt colineare.
Fie triunghiul ABC de laturi a, b, c, G centrul de greutate, I centrul
cercului inscris. Notam![]() = a
= a![]() + b
+ b![]() +c
+c![]() si
si![]() =
= ![]() +
+![]() +
+![]() .
.
Demonstrati ca
vectorii ![]() si
si ![]() sunt colineari si ca
3|
sunt colineari si ca
3|![]() | = (a+b+c)|
| = (a+b+c)| ![]() |.
|.
Solutie
Conform
problemei rezolvate 2) avem relatia a![]() + b
+ b![]() + c
+ c![]() = (a+b+c)
= (a+b+c) ![]() valabila pentru orice punct M din planul triunghiului. Pentru
M
valabila pentru orice punct M din planul triunghiului. Pentru
M![]() G, rezulta: a
G, rezulta: a![]() + b
+ b![]() +c
+c![]() = (a+b+c)
= (a+b+c)![]() , deci
, deci ![]() = (a+b+c)
= (a+b+c)![]() . De asemenea, conform problemei rezolvate 1) avem relatia
. De asemenea, conform problemei rezolvate 1) avem relatia ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() , valabila pentru orice punct M din planul triunghiului.
Pentru M
, valabila pentru orice punct M din planul triunghiului.
Pentru M ![]() I, avem
I, avem ![]() +
+![]() +
+![]() = 3
= 3![]() deci
deci ![]() = 3
= 3![]() = -3
= -3![]() = -
= -![]()
![]() . Prin urmare
. Prin urmare ![]() = -
= -![]()
![]() , relatie ce demonstreaza faptul ca vectorii
, relatie ce demonstreaza faptul ca vectorii ![]() si
si ![]() sunt colineari. De
asemenea |
sunt colineari. De
asemenea |![]() |=
|=![]() |
|![]() |, deci |
|, deci |![]() |=
|=![]() |
|![]() |.
|.
2.7. Probleme propuse
Fie patrulaterul convex ABCD si M, N mijloacele segmentelor [AB] si [CD]. Demonstrati ca:
a) ![]() +
+ ![]() = 2
= 2![]() ;
;
b) ![]() +
+![]() = 2
= 2![]() .
.
Fie paralelogramul ABCD iar O punctul de intersectie al diagonalelor sale. Demonstrati ca:
a) ![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
b) Pentru orice punct M din planul paralelogramului:
![]() +
+ ![]() +
+ ![]() +
+![]() = 4
= 4![]() .
.
Coardele [AB] si [CD] ale cercului de centru O se intersecteaza in
punctul P si sunt perpendiculare. Sa se arate ca ![]() +
+ ![]() +
+ ![]() +
+![]() = 2
= 2 ![]() .
.
In triunghiul ABC semidreapta [AD este bisectoarea unghiului ![]() , DI(BC). Sa se demonstreze ca
, DI(BC). Sa se demonstreze ca ![]() =
= 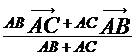 .
.
In triunghiul ABC, semidreptele [AA1, [BB1, [CC1 sunt bisectoare interioare. Sa se arate ca pentru orice punct M din planul triunghiului:
![]() =
= 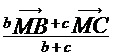 ;
; ![]() =
= 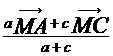 ;
; ![]() =
= 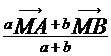 .
.
Triunghiurile ABC si A1B1C1 au
centrele de greutate G, respectiv G1. Demonstrati ca ![]() =
= ![]() (
(![]() +
+![]() +
+![]() ). Deduceti conditia necesara si suficienta ca doua
triunghiuri sa aiba acelasi centru de greutate.
). Deduceti conditia necesara si suficienta ca doua
triunghiuri sa aiba acelasi centru de greutate.
Se considera triunghiul ABC si punctele M I (AB), N I (BC), P I (CA) astfel incat ![]() =
= ![]() =
= ![]() . Aratati ca triunghiurile ABC si MNP au acelasi centru de
greutate.
. Aratati ca triunghiurile ABC si MNP au acelasi centru de
greutate.
Fie ABCD un patrulater fixat si M un punct variabil in plan.
Demonstrati ca vectorul ![]() +
+ ![]() +
+ ![]() +
+![]() trece printr-un punct fix.
trece printr-un punct fix.
Fie ABCDEF un hexagon regulat de latura 1. Sa se calculeze modulul
vectorului ![]() =
= ![]() +
+![]() +
+![]() +
+![]() +
+ ![]() .
.
Fie ABC un triunghi, I centrul cercului inscris iar H ortocentrul.
a) Daca ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() , oricare ar fi M in planul triunghiului, atunci triunghiul
este echilateral;
, oricare ar fi M in planul triunghiului, atunci triunghiul
este echilateral;
b) Daca ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() , oricare ar fi M in planul triunghiului, atunci triunghiul
este echilateral.
, oricare ar fi M in planul triunghiului, atunci triunghiul
este echilateral.
Fie AA1, BB1, CC1 bisectoarele
unghiurilor triunghiului ABC. Aratati ca vectorii ![]() ,
, ![]() ,
, ![]() pot forma un triunghi
daca si numai daca triunghiul ABC este echilateral (vezi problema 4).
pot forma un triunghi
daca si numai daca triunghiul ABC este echilateral (vezi problema 4).
Fie ABC un triunghi, iar O centrul cercului circumscris. Demonstrati
ca triunghiul ABC este echilateral daca si numai daca ![]() +
+![]() +
+![]() =
=![]() .
.
2.8.Descompunerea unui vector dupa doi vectori necolineari,nenuli datti
Notiunea de baza pentru multimea vectorilor liberi din plan se defineste astfel:
Definitie
Cuplul ![]() format din doi vectori
liberi necolineari si nenuli se numeste baza pentru v
format din doi vectori
liberi necolineari si nenuli se numeste baza pentru v
Componentele unui vector intr-o baza
Fie ![]() doi vectori
fixati necolineari,nenuli si
doi vectori
fixati necolineari,nenuli si ![]() un vector arbitrar
(fig.9)
un vector arbitrar
(fig.9)
![]()
![]()
![]()
Consideram reprezentantii ![]() si
si ![]()
Prin punctual M, extremitatea lui![]() ducem paralele a OB respective OA
care intersecteaza OA in M1 si
ducem paralele a OB respective OA
care intersecteaza OA in M1 si
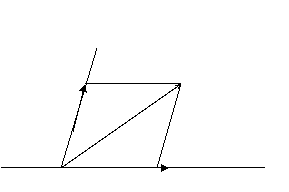
B M
M2
![]() u
u
O ![]() M1 A
M1 A
Fig 9
Avem ![]() (1)
(1)
Vectorii ![]() si
si ![]() sunt colineari, deci
exista
sunt colineari, deci
exista ![]() a.i.
a.i. ![]()
Vectorii ![]() si
si ![]() sunt colineari, deci
exista
sunt colineari, deci
exista ![]() a.i.
a.i. ![]()
Atunci (1) devine ![]() relatii intre vectori legati , sau
relatii intre vectori legati , sau ![]() relatii intre vectori liberi.
relatii intre vectori liberi.
Vectorii ![]()
![]() se numesc componentele vectorului
se numesc componentele vectorului ![]() dupa directiile vectorilor
dupa directiile vectorilor ![]() si
si ![]()
Spunem ca am descompus vectorul ![]() dupa directiile a doi vectori
dupa directiile a doi vectori ![]() si
si ![]()
In egalitatea ![]() , numerele
reale x, y se numesc coordonatele
vectorului liber
, numerele
reale x, y se numesc coordonatele
vectorului liber ![]() in raport cu baza
in raport cu baza ![]()
Scrierea ![]() a lui
a lui ![]() este unica. Intr-adevar daca
este unica. Intr-adevar daca ![]() , atunci
prin scaderea celor doua egalitati se obtine:
, atunci
prin scaderea celor doua egalitati se obtine: ![]() . Daca
am avea
. Daca
am avea ![]() atunci
atunci ![]() ,
relatie ce arata ca vectorii liberi
,
relatie ce arata ca vectorii liberi ![]() si
si ![]() sunt colineari, fals. Prin urmare
sunt colineari, fals. Prin urmare ![]() si apoi
si apoi ![]() si cum
si cum ![]() nu este vector nul rezulta
nu este vector nul rezulta ![]()
Prin urmare am demonstrat urmatoarea:
Fie ![]() o baza pentru v. Atunci orice vector
o baza pentru v. Atunci orice vector ![]() se scrie in mod unic in functie de
vectorii bazei sub forma
se scrie in mod unic in functie de
vectorii bazei sub forma
![]() (spunem ca
(spunem ca ![]() se scrie ca o
combinatie lineara de vectorii bazei)
se scrie ca o
combinatie lineara de vectorii bazei)
Aceasta scriere se numeste scrierea
analitica a vectorului liber ![]() .
.
Numerele reale x, y se
numesc coordonatele vectorului ![]() in baza
in baza ![]() . Notam
. Notam ![]() sau
sau ![]() .
.
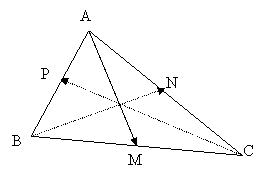 1) Se considera triunghiul ABC si M, N, P mijloacele
laturilor [BC], [AC], [AB]. Sa se descompuna vectorul
1) Se considera triunghiul ABC si M, N, P mijloacele
laturilor [BC], [AC], [AB]. Sa se descompuna vectorul ![]() dupa
directiile vectorilor
dupa
directiile vectorilor ![]() si
si ![]() .
.
Solutie:
Va trebui sa gasim x, yIR a.i.
![]() = x
= x![]() + y
+ y![]()
![]()
![]()
![]()
Rezulta ![]() =
=![]() +
+![]() =
=![]() , deci
, deci ![]() = -
= -![]() -
-![]()
(x=y=-1)
2) Se
considera patratul ABCD si punctele M, N mijloacele laturilor
[BC] si [CD]. Sa se descompuna vectorul ![]() dupa
directiile vectorilor
dupa
directiile vectorilor ![]() si
si ![]() .
.
Solutie:
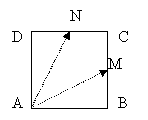 Avem urmatoarele egalitati vectoriale (deduse din
regula triunghiului)
Avem urmatoarele egalitati vectoriale (deduse din
regula triunghiului)
![]()
![]()
Din prima
rezulta ![]() , iar din cea de-a doua
, iar din cea de-a doua ![]() .
.
Prin urmare, ![]() , adica
, adica
![]()
(In baza (![]() ), vectorul
), vectorul ![]() are coordonatele
are coordonatele ![]() ).
).
1) Fie triunghiul ABC si punctele M, N I(BC), PQI(AB) a.i.
![]()
Sa se descompuna vectorii ![]() dupa vectorii
necolineari
dupa vectorii
necolineari ![]() si
si ![]() .
.
2) Fie paralelogramul ABCD de centu O si punctele MI(AB), NI(AD) a.i. ![]() si
si ![]() .
.
Notam ![]() si
si ![]() . Descompuneti vectorii
. Descompuneti vectorii ![]() dupa vectorii necoliniari
dupa vectorii necoliniari ![]() si
si ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |