AUTOPROPULSAREA AUTOMOBILULUI
V-ati pus problema, pana acum, in ce mod sau cum anume se consuma energia dezvoltata de motorul automobilului ? V-ati intrebat cum se transforma si unde regasim aceasta energie? Daca la aceste intrebari nu aveti raspunsuri incercati sa le gasiti in paginile acestui capitol. Studiind paginile urmatoare sper ca veti gasi lamuririle pe care le asteptati.
Automobilul, la pornirea de pe loc sau in timpul deplasarii, intampina o serie de rezistente pe care trebuie sa le invinga cu ajutorul energiei dezvoltate de motor, transmisa la rotile motoare. Marimea, directia si sensul fortelor active si a fortelor de rezistenta care actioneaza asupra automobilului influenteaza caracterul miscarii acestuia.
Definirea conditiilor de autopropulsare si descrierea modului de aparitie a fortelor care se opun inaintarii automobilului sunt necesare, pentru ca, odata cunoscute, sa se poata actiona in sensul micsorarii sau eliminarii lor.
![]()
1. Rezistenta la rulare
In timpul rularii automobilului rotile si calea de rulare se deformeaza . Rotile se deformeaza datorita incarcarii lor cu forte si momente, datorita presiunii interioare a aerului din pneu, datorita materialului si constructiei lor. Deformarea caii de rulare depinde de compozitia materialului sau, de rezistenta invelisului si fundatiei, de marimea fortelor si momentelor cu care rotile automobilului actioneaza asupra sa. Aceste deformatii conduc la consumarea unei parti din energia transmisa de motorul automobilului la rotile motoare, manifestata sub forma unei forte care se opune rularii automobilului, numita rezistenta la rulare.
Rezistenta la rulare-Rr- este o forta cu actiune permanenta, indreptata in sens opus deplasarii automobilului.
Cauzele fizice care genereaza aparitia acestei forte sunt urmatoarele: frecarea dintre pneu si calea de rulare, intrepatrunderea dintre elementele de pneu si microneregularitatile caii de rulare, efectul de ventuza produs de profilele cu contur inchis de pe banda de rulare, frecarile interioare din pneu, deformarea suprafetei caii de rulare, viteza de deplasare a automobilului.
In calculele de proiectare a automobilului rezistenta la rulare este luata in considerare prin coeficientul rezistentei la rulare f, definit prin relatia:
![]() (1.1)
(1.1)
unde. Rr - este rezistenta la rulare;
Ga cosa - este componenta normala pe calea de rulare a greutatii automobilului .
In tabelul 1.1 sunt prezentate valori medii ale coeficientului rezistentei la rulare f pentru diferite categorii de drumuri..
Tabelul 1.1.Valori medii ale coeficientului de rezistenta la rulare f
|
Natura caii |
Starea caii |
Valorile coeficientului f |
|
Sosea de asfalt sau beton |
buna | |
|
satisfacatoare | ||
|
Sosea pietruita |
buna | |
|
Sosea pavata |
stare buna | |
|
cu hartoape | ||
|
Drum de pamant |
uscata-batatorita | |
|
dupa ploaie | ||
|
desfundat | ||
|
Drum cu gheata | ||
|
Drum de zapada |
batatorita |
Pentru calculul rezistentei la rulare, cunoscand marimea coeficientului de rezistenta la rulare f , se utilizeaza relatia:
Rr = f . Ga . cos α [ N ] (1.)
Deoarece pneul
de automobil nu este perfect elastic energia consumata pentru deformarea
elementelor sale componente este mai mare decat energia cedata
a) b)
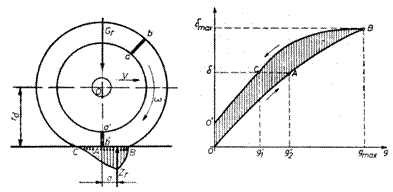
Fig.1.1.Distributia presiunii in suprafata de contact pneu-drum.
in timpul revenirii lor la forma initiala, diferenta transformandu-se in caldura (fenomenul de histerezis). Avand in vedere ca rularea pneului pe drum consta dintr-o succesiune continua de comprimari si destinderi ale elementelor de pneu se poate usor intelege ca diferenta dintre energia consumata la comprimare si cea recuperata la destindere se manifesta prin incalzirea pneului si prin aparitia unei forte rezistente care se opune rularii acestuia.
In figura 1.1.a este prezentat procesul de comprimare si destindere a elementelor unui pneu, prin studiul unui element de lungime initiala ab. La contactul cu drumul in punctul B, elementul de pneu de lungime ab incepe sa se comprime. Comprimarea maxima se produce in punctul A, elementul de pneu avand lungimea minima aIbI. Revenirea la lungimea initiala se face in punctul C, la iesirea din suprafata de contact cu calea de rulare. Daca se noteaza cu δ deformatia elementului ab si cu g sarcina statica pe care acesta o preia, atunci reprezentarea grafica a functiei de dependenta a celor doua marimi este redata in figura 1.1.b Comprimarea este descrisa de curba OAB si corespunde cu deplasarea elementului de pneu pe portiunea BA, din suprafata de contact, iar destinderea, reprezentata de curba BCOI, corespunde deplasarii pe portiunea AC. Se observa ca cele doua curbe OAB si BCOI nu coincid. Pentru aceeasi deformatie δ este necesara, la comprimare, o forta g2 mai mare decat forta g1, pe care o dezvolta elementul elastic la destindere.. Rezulta astfel ca presiunile in partea din fata, pe portiunea AB, a suprafetei de contact pneu-cale sunt mai mari decat presiunile de contact de pe portiunea AC a aceleiasi suprafete. Rezulta ca presiunile de contact dintre pneu si cale vor avea o distributie asimetrica, fig.1.1.a., rezultanta lor, ZR, se va afla pe un suport, deplasat cu distanta a in sensul de mers, fata de axa verticala, care trece prin centrul rotii. Reactiunea ZR genereaza, in raport cu centrul rotii, un moment de rezistenta la rulare a carui valoare se calculeaza cu relatia:
Mrul= ZR· a (1.3)
Aria cuprinsa intre curbele OAB si BCOI reprezinta, la scara, energia consumata la deformarea pneului in timpul deplasarii pe lungimea zonei de contact. Aceasta energie reprezinta energia pierduta prin fenomenul de histerezis, iar prezenta sa fizica se manifesta prin incalzirea pneului in timpul rularii.
Pe langa fenomenul de histerezis la aparitia rezistentei la rulare mai contribuie si alti factori cum sunt: deformarile tangentiale ale anvelopei, frecarea superficiala dintre pneu si calea de rulare, deformarea drumului, efectul de ventuza dintre profilul exterior cu contur inchis al benzii de rulare si cale.
![]()
1.1.Echilibrul rotii nemotoare
Pentru a scoate in evidenta existenta fortei de rezistenta la rulare se studiaza echilibrul rotii nemotoare, conform figurii 1., aplicand metoda izolarii corpurilor. Astfel in articulatia de legatura cu puntea asupra rotoii actioneaza doua forte perpendiculare: greutatea repartizata pe roata -Gr si forta F cu care puntea impinge roata. Ca urmare a actiunii acestor forte in suprafata de contact a rotii cu calea de rulare apar reactiunile drumului asupra rotii: reactiunea normala-Zr, respectiv reactiunea tangentiala- X. Contactul dintre roata si cale se face pe lungimea l, iar forta de contact Zr este rezultanta fortelor de presiune dintre anvelopa si cale. Datorita asimetriei repartitiei fortelor de presiune fata de axa verticala, punctul de aplicare al fortei Zr este deplasat in sensul de inaintare cu distanta a.
![]()
![]()
![]()
 ωR
ωR
Va=ct
![]()
![]()
![]()
![]()
![]() O
F
O
F
![]()
![]() rd Gr Zr
rd Gr Zr
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() X
X
![]() a
a
Fig.1. Echilibrul rotii nemotoare
Ecuatiile de echilibru de forte si momente ale rotii nemotoare, la deplasarea automobilului cu viteza uniforma, sunt urmatoarele:
Zr - Gr
F - X = 0 (1.4.)
Zr . a -X . rd=
Din aceste relatii se poate determina expresia fortei Rr, numita rezistenta la rulare, care apare la roata si care se opune inaintarii sale:
F = X = Zr ·![]() = f ·Zr = Rr (1.5.)
= f ·Zr = Rr (1.5.)
unde raportul ![]() se numeste coeficient de
rezistenta la rulare si se noteaza cu f.
se numeste coeficient de
rezistenta la rulare si se noteaza cu f.
Pentru intregul automobil rezistenta la rulare se calculeaza cu relatia:
Rr = Rri = f Ga (1.6.)
unde: Rri reprezinta rezistenta la rulare la roata "i".
Relatia 1.6. este echivalenta cu relatia 1. prin care a fost introdus coeficientul rezistentei la rulare f.
Pentru un drum in rampa de inclinare rezistenta la rulare se calculeaza cu relatia :
Rr= f Ga cos (1.7.)
![]()
Rezistenta aerului
Rezistenta aerului -Ra- reprezinta
o forta care se opune inaintarii automobilului si apare ca
urmare a interactiunii dintre aer
si automobilul aflat in miscare. Ea este o forta paralela
cu calea de rulare, cu actiune permanenta, de sens opus vitezei
automobilului si are un punct de aplicatie numit centru frontal de
presiune, situat in planul de simetrie longitudinal al automobilului, la
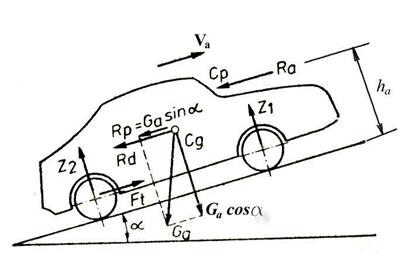
inaltimea ha deasupra drumului, conform figurii 1
Fig.1. Fortele care actioneaza asupra automobilului
Cauzele fizice ale rezistentei aerului sunt urmatoarele: frecarea dintre aer si suprafetele automobilului, repartitia inegala a presiunilor pe partea din fata si spate a caroseriei, energia consumata datorita formarii turbioanelor de aer. Valoarea rezistentei aerului depinde de forma automobilului, de marimea sectiunii transversale a acestuia, de densitatea aerului si de viteza de deplasare.
Marimea rezistentei aerului Ra se determina experimental in tunele aerodinamice. In astfel de instalatii complexe, pe automobile reale sau realizate la o anumita scara de proportionalitate, se analizeaza regimurile de curgere ale curentilor de aer in jurul caroseriei, luandu-se masuri constructive pentru optimizarea curgerii acestora si reducerea posibilitatilor de aparitie a turbioanelor.
Din mecanica fluidelor se stie ca rezistenta cu care aerul se opune inaintarii unui corp in miscare, avand viteze similare automobilului (0-330 m/s) este proportionala cu densitatea aerului ρ,cu aria sectiunii transversale maxime A a automobilului si cu patratul vitezei de deplasare Va a acestuia:
![]()
![]() [ N ] (1.)
[ N ] (1.)
unde: ρ 1,225 [kg/m3]-densitatea aerului;
cx - coeficientul de rezistenta a aerului;
A - aria sectiunii transversale maxime [m2];
Va- viteza de deplasare a automobilului in raport cu aerul ambiental[m/s]
Notand produsul constant:
![]() [kg/m3] ()
[kg/m3] ()
numit coeficient aerodinamic, rezistenta aerului este data de relatia:
Ra = K . A . V2 a [ N ] (3.)
(in conditii atmosferice standard K = 0,6125 Cx kg/m3)
Aria transversala maxima se determina, cu suficienta precizie (erori sub 5%), dupa desenul de ansamblu al automobilului in vederea frontala, utilizand relatia:
A = B . H [ m2 ] (4.)
unde : B este ecartamentul automobilului [m];
H este inaltimea automobilului [m].
Ca metoda de alegere a marimii coeficientului de rezistenta a aerului Cx (sau a coeficientului aerodinamic K ) in bibliografia de specialitate sunt prezentate
date experimentale pentru automobile cu forma apropiata de cea a unui nou automobil care, eventual, trebuie proiectat. In acest sens in tabelele 1.si sunt cuprinse asemenea date pentru diverse categorii de automobile.
Tabelul 1.Valori ale coeficientului de rezistenta a aerului pentru autoturisme
|
Nr. crt. |
Tipul autoturismului |
Cx |
Nr. crt. |
Tipul autoturismului |
Cx |
|
Audi 1000 Coupe |
Porsche 911 | ||||
|
BMW 1500 |
Porsche 904 GTS | ||||
|
Citroen DS+19 |
Renault R8 | ||||
|
Nr. crt. |
Tipul autoturismului |
Cx |
Nr. crt. |
Tipul autoturismului |
Cx |
|
Ferrari 250 GT |
Skoda Favorit | ||||
|
Ford 17 MP3 |
Volkswagen 1200 | ||||
|
Ford Falcon |
Volvo 12 S | ||||
|
Ford Mustang |
Dacia 1300 |
|
|||
|
Jaguar MK+TV |
Oltcit Club |
Tabelul Valori ale coeficientului de rezistenta a aerului pentru autoturisme, autocamioane si autobuze
|
Tipul automobilului |
A m2 |
Cx |
|
Automobil de curse | ||
|
Autoturism cu caroserie inchisa | ||
|
Autoturism cu caroserie deschisa | ||
|
Autobuz | ||
|
Autocamion cu platforma deschisa | ||
|
Autotren rutier, cu doua elemente caroserie platforma | ||
|
Autofurgon | ||
|
Autotren rutier, cu doua elemente caroserie furgon |
![]()
3. Rezistenta la demarare
Regimurile tranzitorii ale miscarii automobilului sunt caracterizate de modificarea vitezei de deplasare, prin accelerare sau franare. Rezistenta la demarare -Rd- este o forta care se opune inaintarii automobilului si se manifesta in regimul de miscare accelerata. Ea apare ca urmare a inertiei de translatie sau de rotatie cu care piesele automobilului, prin masa lor, se opun accelerarii sale. In regimul franarii inertia pieselor automobilului devine o forta activa, care tinde sa mentina deplasarea automobilului si contribuie la marirea spatiului sau de franare.
La miscarea accelerata a automobilului masa sa totala, in miscare de translatie cu acceleratia a, se opune miscarii cu o forta de inertie FI =--ma.a, iar piesele care executa miscare de rotatie se opun cu momentul de inertie Mi , dat de produsul dintre momentul de inertie masic J si acceleratia unghiulara , adica : Mi= - J .
Daca se noteaza cu Rd forta rezistenta totala la demarare, atunci expresia ei va fi:
Rd = Rdt + Rdr (3.1.)
unde: Rdt este forta de inertie datorata masei totale a automobilului aflat in miscare accelerata de translatie;
Rdr este forta de rezistenta datorata inertiei pieselor in miscare de rotatie.
Rezistenta la demarare Rdt se calculeaza cu relatia:
Rdt = ma .
![]() = ma . a (3.)
= ma . a (3.)
unde: ma este masa totala a automobilului;
![]() =
a reprezinta acceleratia automobilului.
=
a reprezinta acceleratia automobilului.
Pentru calculul rezistentei la demarare, generata de masele in miscare de rotatie se vor inlocui toate aceste mase cu o singura masa de translatie, ipotetica, numita masa redusa, mred , care are proprietatea ca la viteza oarecare V de deplasare a automobilului are aceeasi energie cinetica cu energia cinetica a tuturor maselor aflate in miscare de rotatie. Daca se noteaza cu Ji momentul masic al unei piese 'i' a transmisiei, inclusiv momentul de inertie masic al motorului redus la arborele cotit, cu ωi viteza unghiulara de rotatie a acesteia, cu ηt randamentul transmisiei pana la rotile automobilului, cu Jr momentul de inertie masic al unei roti si cu ωr viteza unghiulara a rotilor motoare, relatia de echivalenta devine:
![]() =
= ![]() (3.3.)
(3.3.)
Randamentul ηt care afecteaza energia piesei oarecare 'i' in miscare de rotatie, exprima faptul ca nu toata energia acesteia ajunge la rotile motoare ale automobilului, o parte pierzandu-se in transmisie prin frecari.
Relatia de legatura intre viteza automobilului Va si viteza unghiulara ωi a piesei care executa miscare de rotatie, este de forma:
![]()
unde : ωR este viteza unghiularta a rotii motoare;
iti este raportul de transmitere intre piesa arecare 'i' si rotile motoare.
Daca se inlocuieste relatia 3.4. in 3.3., dupa simplificari, se obtine:
![]() (3.5.)
(3.5.)
Rezistenta la demarare datorata maselor in miscare de rotatie-Rdr se va calcula cu relatia:
Rdr= mred.![]() (3.6.)
(3.6.)
Tinand seama de relatiile 3., 3.5. si 3.6. pentru calculul rezistentei la demarare Rd relatia 3.1. devine:
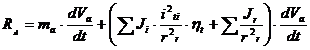 (3.7.)
(3.7.)
Dand factor comun ![]() se obtine:
se obtine:
![]() (3.8.)
(3.8.)
unde s-au notat prin λ si ρ rapoartele adimensionale:
![]() ;
; ![]() (3.9.)
(3.9.)
Raportul λ reprezinta influenta pieselor transmisiei automobilului care executa miscare de rotatie, inclusiv momentul de inertie masic al motorului redus la arborele cotit.
Raportul ρ reprezinta aceeasi influenta exercitata de rotile automobilului.
Se defineste coeficientul de influenta a maselor aflate in miscare de rotatie, δ, prin expresia:
δ = 1+ (3.10)
Din ultimele doua relatii se poate constata ca valoarea coeficientului δ se va modifica odata cu schimbarea treptelor de viteze, datorita marimilor iti, Ji.
Pentru calculul rezistentei la demarare este necesara cunoasterea marimii coeficientului δ in fiecare treapta de viteze
Ca modalitate de alegere a marimii coeficientului bibliografia de specialitate recomanda mai multe metode:
a) utilizarea, daca se dispune din studiul solutiilor similare a valorilor corespunzatoare automobilelor cu caracteristicile cele mai apropiate. In acest caz se estimeaza pe baza schemei din fig.3.1. valoarea coeficientului d in prima treapta a cutiei de viteze, cu relatia:
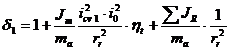 (3.11.)
(3.11.)
unde:
Jm - este momentul masic de inertie al pieselor motorului reduse la arborele primar al cutiei de viteze [kg.m2];
JR- momentul mastic de inertie al unei roti [kg.m2];
icv 1- raportul de transmitere al primei trepte din cutia de viteze;
i0- raportul de transmitere al transmisiei principale;
ht- randamentul transmisiei;
rr- raza de rulare a rotilor [m].
![]()
![]()
Fig.3.1. Modelul dinamic simplificat al
autovehiculului
![]()
![]()
![]()
![]() iCVK
iCVK
![]()
![]()
![]() Im
io
Im
io
![]()
![]()
![]()
![]()
![]()
Pentru celelalte trepte, grupand constantele, se obtine relatia de calcul:
![]() (3.12)
(3.12)
unde:
![]() si
si 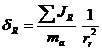 (3.13)
(3.13)
b) Utilizarea de valori medii functie de tipul si caracteristicile automobilului din datele statistice cuprinse in tabelele 3.1. si
Tabelul 3.1. Valori ale coeficientilor maselor in miscare de rotatie
|
Tipul automobilului |
Momentele de inertie [kg.m2]; |
icv 1 |
io |
d |
|
|
Im |
Ir |
||||
|
Autoturisme | |||||
|
Autobuze, autocamioane | |||||
Tabelul 3.Valori ale coeficientilor maselor in miscare de rotatie
|
Tipul automobilului |
dM |
dR |
icv 1 |
|
Autoturisme | |||
|
Autobuze, autocamioane |
c) In bibliografia de specialitate pentru calculul coeficientului δk se recomanda si relatia:
δk=1+σ۰i2CVk (3.14.)
in care: σ =0,04-0,09;
iCVk-raportul de transmitere in treapta k a cutiei de viteze.
In concluzie trebuie precizat faptul ca indiferent de metoda folosita pentru determinarea coeficientului δ de influenta a maselor in miscare de rotatie rezistenta la demarare Rd se calculeaza cu relatia:
Rd = ![]() =
=![]() [N] (3.15.)
[N] (3.15.)
unde: ma reprezinta masa totala a automobilului [kg];
Ga reprezinta greutatea totala a automobilului [N];
![]() reprezinta acceleratia automobilului [
reprezinta acceleratia automobilului [![]() ].
].
Observatii:
a) In regimul franarii rezistenta la demarare devine o forta activa,
actionand in sensul deplasarii automobilului.
b) In cazul franarii cu motorul decuplat inertia masei de translatie nu este
influentata de momentul masic de inertie al motorului. Ca urmare in relatiile de mai sus Jm = δm=0.
c) Forta Rd de rezistenta la demararea automobilului se considera ca are punctul de aplicare in centrul de greutate al automobilului.
![]()
4. Rezistenta la panta
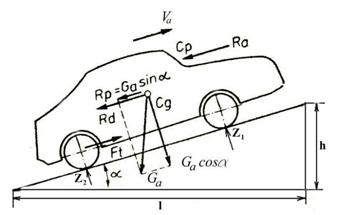
La deplasarea automobilului pe drumuri cu inclinarea
longitudinala α, figura 4.1., greutatea sa totala Ga
, al carei punct de aplicare se afla in centrul de greutate cg,
se descompune astfel: o componenta perpendiculara pe calea de
rulare-Ga .cosα si una paralela cu aceasta- Ga
. sinα. Componenta paralela cu calea de rulare, numita rezistenta la panta -Rp
se opune inaintarii automobilului pe rampa. Daca automobilul
coboara panta atunci componenta Ga . sinα. devine
forta activa, care contribuie la deplasarea automobilului.
Fig.4.1.Rezistentele la inaintarea automobilului
Expresia de calcul a rezistentei la panta este data de relatia:
Rp =![]() Ga sin a [N (4.1)
Ga sin a [N (4.1)
unde: α este unghiul de inclinare al caii de rulare in plan longitudinal.
Observatie: semnul " se foloseste la urcarea rampelor, iar semnul " " la coborarea pantelor.
Pentru pante cu inclinari mici la care eroarea aproximarii :
sina ≈ tga este sub 5% ,panta se exprima in
procente: p % = tga =![]() (fig.4.1.)
(fig.4.1.)
In acest caz expresia rezistentei la panta se calculeaza cu relatia:
Rp = Ga . p [N (4.)
In tabelul 4.1. sunt prezentate valori medii si maxime admise pentru unghiul rampei in functie de tipul automobilului.
Tabelul 4.1.Valori medii si maxime ale unghiului de inclinare longitudinala a caii de rulare
|
Tipul automobilului |
Valori medii |
Valori maxime |
|
Autovehicule cu o punte motoare |
17o - 19o |
22o |
|
Autovehicule cu tractiune integrala cuplata |
28o - 32o |
35o |
Deoarece rezistenta la rulare Rr cat si rezistenta la panta Rp sunt determinate de starea si caracteristicile caii de rulare, se defineste forta de rezistenta totala a caii -Rψ, calculata cu relatia:
Rψ = Rr + Rp = Ga( f cosa +sina ) = Ga . y [N (4.3.)
unde : f . cos a + sin a = y este coeficientul rezistentei totale a caii de rulare.
Puterile consumate pentru invingerea rezistentelor la inaintare, respectiv puterea pentru invingerea rezistentei la rulare Pr, puterea pentru invingerea rezistentei la aerului Pa , puterea pentru invingerea rezistentei la demarare Pd si puterea consumata pentru invingerea rezistentei la panta Pp se calculeaza cu relatiile:
Pr = Va. Rr = Va.f.Ga.cosα [W]
Pa= Va. Ra = k.A. Va3 [W]
(4.4.)
Pd = Va. Rd
= Va. δ . ma .![]() [W]
[W]
Pp = Va. Rp = Va.Ga. sinα [W]
![]()
5. Momentul la roata motoare- MR
Schema de principiu a transmisiei unui automobil este prezentata in figura 5.1. In regimul nominal de functionare motorul M dezvolta puterea efectiva Pe, momentul motor efectiv Me si turatia efectiva ne. Prin intermediul transmisiei, alcatuita din ambreiajul A, cutia de viteze CV, transmisia longitudinala TL si puntea motoare PM fluxul de putere al motorului ajunge la rotile motoare RM,
unde regasim puterea la roata PR, momentul motor la roata MR si turatia rotii
Pe, Me, ne icv
![]()
Va M A CV TL TP PM
io, PM
![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() RM (PR, MR, n)
RM (PR, MR, n)
Fig.5.1.Schema transmisiei unui automobil
motoare nR. Daca ambreiajul A are rolul sa cupleze sau sa decupleze transmisia de motor, in cutia de viteze CV are loc o prima multiplicare a momentului motor dezvoltat de motorul automobilului si demultiplicarea turatiei, cu o valoare egala cu marimea raportului de transmitere al treptei de viteze cuplate cu itr>1 (demultiplicarea momentului si multiplicarea turatiei se produce numai la cuplarea treptei de viteze cu raportul de transmitere subunitar). Transmisia longitudinala TL, cu raportul de transmitere mediu unitar, are rolul sa transmita fluxul de putere intre doi arbori neconcurenti, de la cutia de viteze CV la transmisia principala TP. Aceasta are raportul de transmitere iO (iO > 1) si este montata in puntea motoare PM. De la transmisia principala fluxul de putere ajunge, prin intermediul diferentialului, la rotile motoare RM.
Datorita frecarilor care apar intre elementele transmisiei (frecarile din lagare, frecarile cu elementele de etansare, pierderile prin barbotarea uleiului din cartere) la rotile motoare ale automobilului nu ajunge toata puterea dezvoltata de motor, o parte din aceasta pierzandu-se pe transmisie. Daca se noteaza cu ηt randamentul total al transmisiei puterea PR disponibila la rotile motoare se poate calcula cu relatia:
PR = ηt.Pe = ηt.Me.ωe (5.1.)
unde: Pe, Me, si ne reprezinta, respectiv, puterea efectiva, momentul efectiv si turatia efectiva a motorului automobilului.
Viteza unghiulara a rotilor motoare ωR se calculeaza in functie de viteza unghiulara a motorului ωe, cunoscand raportul total de transmitere al transmisiei it= iCV .iCD . iO, astfel:
ωR = ![]() =
= ![]() (5.)
(5.)
unde iCD reprezinta raportul de transmitere al cutiei de distributie sau reductorului central ( daca acestea sunt montate pe transmisie).
Cunoscand puterea la roata motoare PR calculata cu rel.5.1. si viteza unghiulara a rotii motoare ωR, data de rel.5., se poate calcula marimea momentului motor MR, care antreneaza rotile motoare ale automobilului cu relatia:
MR = ![]() = Me . iCV . iCD . iO . ηt (5.3.)
= Me . iCV . iCD . iO . ηt (5.3.)
Din rel.5.3. se poate observa ca momentul motor MR la roata de propulsie a automobilului este mai mare decat momentul motorului Me avand in vedere ca produsul it = iCV . iCD . iO >> 1 iar ηt =0,82-0,93.
![]()
6.Echilibrul rotii motoare
Pentru studiul echilibrului rotii motoare a automobilului se aplica metoda izolarii corpurilor, fig.6.1.,. La deplasarea automobilului cu viteza constanta, Va=ct, asupra rotii motoare actioneaza momentul motor MR , cu care arborele planetar antreneaza roata motoare, iar articulatia de legatura a rotii cu puntea este inlocuita cu doua forte perpendiculare: sarcina verticala care revine rotii-Gr si forta de tractiune Ft ,cu care puntea se opune inaintarii rotii motoare. Ca urmare a actiunii momentului la roata si a fortelor mai sus amintite in suprafata de contact a rotii cu calea de rulare apar, respectiv, reactiunile normala-Zr si tangentiala-X.
![]()
![]() MR
MR

![]()
![]() ωR
ωR
![]() Va
Va
![]()
![]()
![]()
![]()
![]() Ft O
Ft O
![]()
![]() rd Gr Zr
rd Gr Zr
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() X
X
![]() a
a
Fig.6.1. Echilibrul rotii motoare
In suprafata de contact dintre roata si cale reactiunea verticala Zr reprezinta rezultanta fortelor de presiune dintre anvelopa si cale. Datorita asimetriei repartitiei fortelor de presiune pe lungimea suprafetei de contact (cauzata de fenomenul de histerezis), forta verticala rezultanta este deplasata, spre sensul de inaintare, cu distanta a.
Ecuatiile de echilibru de forte si momente ale rotii motoare, la deplasarea automobilului cu viteza constanta, sunt urmatoarele:
ΣFx = 0, adica:
X - Ft = 0
ΣFy= 0, adica: (6.1.)
Zr - Gr = 0
ΣMO = 0, adica:
X . rd Zr . a - MR = 0
Din ultima relatie rezulta:
X = ![]() (6.)
(6.)
In mod conventional se defineste forta la roata FR forta rezultanta a eforturilor de frecare dintre pneu si calea de rulare, care ar produce asupra rotii acelasi efect pe care-l produce momentul motor aplicat rotii motoare Mr, adica:
FR = ![]() (6.3.)
(6.3.)
Ca
si in cazul rotii nemotoare ( subcapitolul 1.1.) raportul ![]() este numit coeficient de rezistenta la
rulare si se noteaza cu f.
Cu aceasta observatie, tinand seama de relatiile 6.1.
si 6. se ajunge la expresia:
este numit coeficient de rezistenta la
rulare si se noteaza cu f.
Cu aceasta observatie, tinand seama de relatiile 6.1.
si 6. se ajunge la expresia:
Ft= FR - f . Gr = FR - Rr (6.4.)
unde: Rr = f . Zr este rezistenta la rulare (Gr =Rr).
Din relatia 6.4. se observa ca forta de tractiune Ft, cu care roata motoare impinge puntea automobilului (asigura propulsarea automobilului), este data de diferenta dintre forta la roata FR, generata de momentul la roata MR si rezistenta la rulare Rr, proprie rotii motoare.
![]()
7. Ecuatia generala de miscare rectilinie
a automobilului si bilantul sau de tractiune
Pentru stabilirea ecuatiei de miscare se ia in considerare automobilul in deplasare rectilinie, pe o cale cu inclinare longitudinala a, in miscare accelerata, fig.4.1. Automobilul se deplaseaza sub influenta fortei de tractiune Ft si a fortelor de rezistenta, la demarare -Rd, la panta- Rp si a aerului -Ra.
Ecuatia de echilibru de forte de-a lungul caii de rulare poate fi scrisa sub forma:
Ft - Rr -Rd -Rp -Ra = 0 (7.1)
Inlocuind forta de tractiune Ft cu valoarea data de relatia 6.4., se obtine:
FR - Rr -Rd -Rp -Ra = 0 (7.)
in care forta la roata FR se calculeaza cu relatia:
![]() (7.3.)
(7.3.)
In relatia 7.3. semnificatia notatiilor este urmatoarea:
-Me este momentul efectiv al motorului;
-it= iCV .iCD. i o , reprezinta raportul total de transmitere al transmisiei;
-![]() t este randamentul transmisiei;
t este randamentul transmisiei;
-rd este raza dinamica a rotii automobilului.
Introducand expresiile rezistentelor la inaintare relatia 7. devine:
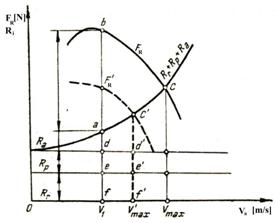
Fig.7.1. Bilantul de tractiune al automobilului
FR = f . Ga .
cos α +Ga . sin α + k . A .V2 +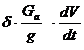 (7.4.)
(7.4.)
Relatia 7.4. reprezinta ecuatia de miscare rectilinie a automobilului. Ea este o ecuatie diferentiala de ordinul I. Cu ajutorul acestei relatii se determina bilantul de tractiune al automobilului, care defineste echilibrul tuturor fortelor care actioneaza asupra automobilului in miscare rectilinie, motorul functionand la admisie totala. Forta totala la roata FR, obtinuta prin insumarea fortelor tangentiale de la toate rotile motoare ale automobilului, echilibreaza suma fortelor rezistente, care se opun inaintarii automobilului.
Reprezentand grafic relatia 7.4. se obtine diagrama bilantului de tractiune, pentru o treapta oarecare din cutia de viteze, functie de viteza de deplasare a automobilului (fig.7.1.)
Pentru o viteza V1 a automobilului segmentul fe reprezinta, la scara, marimea rezistentei la rulare Rr, segmentul ed reprezinta marimea rezistentei la panta Rp, segmentul da reprezinta marimea rezistentei aerului Ra iar segmentul ab reprezinta marimea rezistentei la demarare Rd sau disponibilul de forta pentru accelerare. La intersectia dintre suma rezistentelor la inaintare Rr + Rp+ Ra si curba fortei la roata FR, in punctul c, rezulta viteza maxima Vmax a automobilului, cand disponibilul de forta pentru accelerare devine nul (Rd = 0).La admisie partiala a motorului forta la roata s-a notat cu FRI ( curba cu linie intrerupta).
Cazuri particulare ale ecuatiei de miscare a automobilului
a) deplasarea cu viteza maxima:
La deplasarea automobilului cu viteza maxima, pe un drum orizontal, rezistenta la panta Rp si forta disponibila pentru accelerare sunt nule, astfel incat relatia 7.4. devine:
![]() (7.5.)
(7.5.)
b) deplasarea pe calea de rulare cu inclinarea longitudinala maxima sau pe calea cu rezistenta specifica maxima.
In acest caz coeficientul rezistentei totale a drumului y ia forma:
y ymax= f .cos αmax + sin αmax, iar relatia 7.4. ia forma urmatoare:
![]() (7.6.)
(7.6.)
unde: FRI max este forta la roata maxima in prima treapta a cutiei de viteze;
VI min reprezinta viteza minima stabila a automobilului in prima treapta a cutiei de viteze.
La deplasarea pe rampa maxima, cu viteza minima stabila in treapta I a cutiei de viteze, rezistenta aerului Ra se poate neglija, ca fiind foarte mica, in comparatie cu celelalte forte, care se opun inaintarii automobilului, rezultand o alta forma a ecuatiei de miscare a, specifica acestui regim de deplasare:
![]() (7.7.)
(7.7.)
c) pornirea din loc cu acceleratia maxima pe drum orizontal:
In acest caz rezistenta la panta Rp , ca si rezistenta aerului Ra, sunt nule, deci ecuatia generala de miscare ia forma particulara:
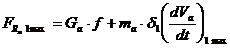 (7.8.)
(7.8.)
unde 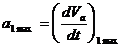 este acceleratia maxima in prima treapta a
cutiei de viteze.
este acceleratia maxima in prima treapta a
cutiei de viteze.
O alta forma a ecuatiei de miscare a automobilului este data de relatia 7.9., din care se poate calcula acceleratia automobilului:
![]() (7.9.)
(7.9.)
sau:
![]() (7.10)
(7.10)
Pentru a obtine bilantul de putere al automobilului, care reprezinta echilibrul dintre puterea la roata PR si suma puterilor necesare invingerii rezistentelor la inaintare, in relatia 7.4. se inmultesc ambii membri ai ecuatiei cu termenul Va (viteza automobilului), rezultand:
PR = FR . Va = Va . Ga . f . cosα +Va
.Ga.sinα +k.A.V3a+Va.![]() (7.11.)
(7.11.)
Curbele de variatie a puterii efective a motorului Pe , puterii la roata PR si a celorlalte puteri necesare invingerii rezistentelor la inaintare (Pr-puterea consumata pentru invingerea rezistentei la rulare, Pp- puterea consumata pentru invingerea rezistentei la panta, Pa- puterea consumata pentru invingerea rezistentei aerului, Pd- puterea consumata pentru invingerea rezistentei la demarare) reprezinta, pentru o treapta oarecare din cutia de viteze, bilantul de putere al automobilului, fig. 7.
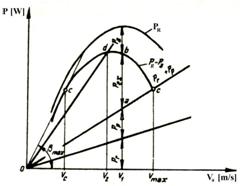
Fig.7.Bilantul de putere al automobilului
Bilantul de putere se foloseste pentru calculul puterii transmise la rotile motoare, in diferite regimuri de deplasare ale automobilului.
Cazuri particulare de folosire a bilantului de putere:
a) deplasarea cu viteza maxima, pe cale orizontala:
PRVmax = f . Ga .Vmax +k .A .V3max (7.1)
b) deplasarea pe calea de rulare cu rezistenta specifica maxima:
PR max =
Ga .ψmax.VI max +![]() (7.13.)
(7.13.)
unde: VI max este viteza maxima in prima treapta a cutiei de viteze.
c) pornirea din loc cu acceleratia maxima pe drum orizontal:
PR
a max =Ga .VI max.f
+ ![]() (7.14.)
(7.14.)
unde:
![]() = a I max este acceleratia maxima in prima
treapta a cutiei de viteze.
= a I max este acceleratia maxima in prima
treapta a cutiei de viteze.
![]()
8.Forte de contact intre pneu si calea de rulare
Atat in cazul rotilor nemotoare (subcapitolul 1.1.) cat si in cazul rotilor motoare (subcapitolul 6.) reactiunea tangentiala longitudinala, notata cu X,. paralela cu calea de rulare, poarta numele de forta de aderenta.
La deplasarea automobilului pe cai de rulare nedeformabile forta de aderenta se confunda, in general, cu forta de frecare dintre pneu si cale. In realitate ea are o geneza mai complexa, fiind influentata de intrepatrunderea dintre elementele de pneu si drum, de deformabilitatea drumului, de adancimea de patrundere a pneului in straturile deformabile ale caii de rulare.
Prin analogie cu forta de frecare, marimea fortei de aderenta depinde de marimea fortei verticale Zr care actioneaza asupra rotii si de natura suprafetelor de frecare.
In orice conditii de deplasare, legate de starea pneurilor, de starea drumului si de regimul de miscare al automobilului, forta de aderenta X nu poate depasi o anumita valoare limita, fara ca roata sa nu alunece sau sa patineze.
Valoarea maxima a fortei X se numeste aderenta si se noteaza cu Xmax
Raportul dintre aderenta si reactiunea normala a drumului asupra rotii se numeste coeficient de aderenta si se noteaza cu φ:
![]() (8.1.)
(8.1.)
Coeficientul de aderenta φ este o marime care se determina experimental. Valorile medii ale coeficientului de aderenta sunt redate in tabelul 8.1. La rularea automobilului pe drumuri umede aderenta pneurilor cu calea de rulare scade. In aceste situatii, la deplasarea cu viteze ridicate, datorita interpunerii intre pneu si cale a unei pelicule de lichid, care nu este eliminata de sub anvelopa, se poate pierde complet contactul dintre pneu si cale, aderenta devenind nula. Fenomenul este cunoscut sub numele de hidroplanare sau acvaplanare, iar viteza de deplasare a automobilului, la care pelicula de fluid patrunde complet sub pneu, se numeste viteza critica de hidroplanare.
Tabelul 8.1.Valori ale coeficientului de aderenta φ
|
Caracteristicile drumului |
Calitatea drumului |
|
|
Uscata |
Umeda |
|
|
Beton Beton asfaltat Pavele de piatra Nisip tasat Pamant tasat Zapada batuta Polei | ||
Din relatia 6., de la echilibrul rotii motoare, se poate deduce expresia:
MR = rd . ( X + f .Zr ) (8.)
Aceasta ecuatie reprezinta expresia momentului la roata MR aplicat rotii in functie de forta de aderenta X si de rezistenta la rulare Rr = f .Zr. Deoarece forta de aderenta are o valoare maxima data de expresia Xmax = φ . Zr, rezulta ca si momentul transmis rotii motoare trebuie sa nu depaseasca o anumita valoare maxima, pentru a nu aparea patinarea rotii.
Tinand seama de relatiile 8.1 si 8.2 se determina expresia momentului maxim la roata, la limita aderentei cu relatia:
MR
max = rd ![]() (8.3)
(8.3)
In cazul in care aderenta este nula, momentul minim la roata , MR min necesar pentru a invinge momentul dat de rezistenta la rulare, va fi:
MR min= rd . f . Zr (8.4)
Se poate afirma ca momentul aplicat rotii motoare poate lua valori cuprinse intre o valoare maxima, data de relatia 8.3 si o valoare minima, data de relatia 8.4. Daca valoarea acestui moment depaseste valoarea maxima MRmax apare alunecarea (patinarea) rotilor motoare, cu pierderea stabilitatii automobilului. Alunecarea rotii motoare are o influenta importanta asupra coeficientului de aderenta, fapt ce poate fi observat in graficul din figura 8.1. Se observa ca la valori mici ale alunecarii " a"(20-30%) coeficientul de aderenta are o valoare maxima si scade apoi, cu cresterea alunecarii.
φ 0,8
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() 0,6
0,6
![]() 0,4
0,4
0,2 0,2 0,4 0,6 0,8 1 a
Fig.8.1.Variatia coeficientului de aderenta in functie de alunecarea rotii
Marimea coeficientului de aderenta φ este influentata de viteza de deplasare a automobilului, de calitatea pneului si a drumului, de presiunea interioara a aerului din pneu, de sarcina verticala care revine rotilor motoare.
![]()
8.1.Cercul aderentei si elipsa de echiaderenta
Daca momentul motor MR care actioneaza asupra rotii motoare genereaza forta tangentiala longitudinala X si asupra rotii actioneaza si forta transversala Fy, fig.8.2, atunci reactiunea caii de rulare va avea si o componenta transversala Y (Y=Fy). Rezultanta R a fortelor de aderenta longitudinala si transversala nu va putea depasi aderenta permisa de calea de rulare si de incarcarea verticala a rotii, adica:
![]() ≤
≤ ![]() (8.5.)
(8.5.)

![]() Fy
Fy
Fx
R
Fig.8.Incarcarea rotii motoare
Oricare ar fi raportul dintre marimile X si Y, rezultanta lor va fi raza cercului, de marimea φ . Zr , numit cercul aderentei, a carei ecuatie este data de relatia urmatoare:
X2 + Y2 = φ2 . Z2r = R (8.6.)
Se
observa ca pe masura ce momentul motor la roata Mr
creste va creste si componenta longitudinala X a
aderentei, iar componenta laterala Y se va micsora (figura 8.3.)
La limita, daca forta de aderenta longitudinala X
ia valoarea maxima, adica X = Xmax = .Zr , rezulta
ca Y = 0., ceea ce inseamna ca roata nu mai poate prelua
forte laterale fara ca sa derapeze. Componenta
transversala Y a aderentei se numeste forta de ghidare laterala a rotii . Ea poate
aparea la deplasarea rectilinie a automobilului, fiind cauzata de
vant lateral sau de inclinarea transversala a drumului sau la deplasarea
automobilului in viraj, datorita actiunii
fortei centrifuge
si se opune deplasarii
laterale a acestuia,. De aici rezulta ca, in cazul rotilor
motoare sau a celor franate, incarcate cu moment motor, respectiv, cu
moment de franare, posibilitatile de ghidare laterala a
automobilului scad. In cazul unor accelerari sau decelerari intense
in viraje poate apare deraparea automobilului, prin cresterea fortei
longitudinale X si micsorarea fortei de ghidare laterala Y.
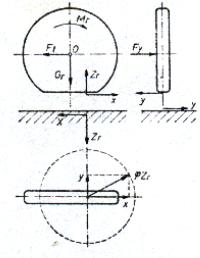
Fig.8.3.Cercul aderentei Fig.8.4. Elipsa de echiaderenta
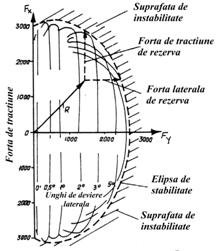
Avand in vedere raportul real existent intre marimea fortelor longitudinale si transversale existente in suprafata de contact a pneului cu calea de rulare se aminteste tot mai des de regula incadrarii lor intr-o elipsa de echiadarenta, fig.8.4., avand in ordonata forta longitudinala de tractiune Ft si in abscisa forta transversala Fy. Se observa ca la cresterea unghiului de deviere laterala a pneului axa orizontala a elipsei creste mai repede decat axa verticala, ceea ce poate conduce, la limita, la iesirea fortei rezultante R din interiorul elipsei de stabilitate si la pierderea controlului automobilului. In anumite conditii de deplasare, cand rezultanta R are o valoare mai mica decat valoarea maxima data de elipsa de echiaderenta, raman, sub forma fortelor de rezerva (trasate cu linie intrerupta), disponibilitati marite de preluare a unor forte longitudinale si transversale. Cele doua forte sunt dependente una de alta, in sensul ca atunci cand una creste cealalta scade, marimea rezultantei ramanand constanta. Astfel la cresterea fortei de tractiune se reduce rezerva fortei laterale, iar la cresterea fortei laterale, cum este cazul inscrierii automobilului in viraj cu viteze ridicate, se reduc fortele de tractiune de rezerva.
Asupra fortelor longitudinale si transversale controlul se poate face in mod diferit, in functie de caracteristica de generare a acestor forte. Daca asupra fortelor longitudinale, de tractiune sau de franare, se poate efectua un control permanent, prin introducerea sistemelor de control al tractiunii sau franarii comandate electronic (ASR, ABS, etc) , asupra fortelor transversale se poate interveni mai putin, ele depinzand de stilul de conducere al conducatorului automobilului si de viteza de deplasare.
![]()
9. Reactiunile normale ale caii de rulare asupra puntilor automobilului
Reactiunile normale ale caii de rulare asupra puntilor automobilului au un rol important in determinarea aderentei, asupra performantelor de demarare, de franare sau asupra stabilitatii.
Marimea reactiunilor normale este conditionata de repartitia statica a maselor automobilului pe punti, repartitie care depinde de pozitia centrului de greutate si de inclinarea caii de rulare. In deplasarea automobilului reactiunile normale se modifica in functie de caracteristicile regimului de deplasare (accelerare sau franare) si de caracteristicile drumului (drum inclinat sau in viraj).
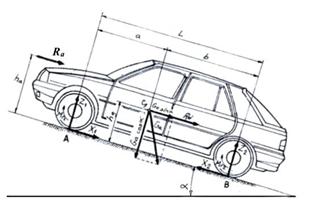
In cele ce urmeaza se studiaza trei cazuri de automobile
aflate pe cai de rulare cu inclinarea longitudinala α, avand
puntea motoare in spate, in fata sau ambele punti motoare. Fig.9.1.Automobil cu puntea motoare in spate
Pentru determinarea reactiunilor normale ale caii de rulare in conditii dinamice se analizeaza, mai intai, cazul automobilului care se deplaseaza cu viteza uniform accelerata, pe o rampa de unghi α, avand puntea motoare in spate. Asupra sa actioneaza rezistentele la inaintare si forta de tractiune, conform figurii 9.1. Scriind ecuatiile de momente in raport cu punctele A si B se obtin expresiile urmatoare:
Z1 L + ( Mr1+ Mr 2) +Ra ha +Rd hg
+ hg Ga sin ![]() -b Ga cos
-b Ga cos![]() =0 (9.1)
=0 (9.1)
si
Z2 L-(Mr 1+ Mr 2) - Ra ha -Rd hg-
Ga hg sin ![]() -a.Ga.cosα = 0 (9.)
-a.Ga.cosα = 0 (9.)
in care: Z1, Z2 sunt reactiunile verticale dinamice la puntea fata, respectiv la puntea din spate; Mr 1, Mr 2 sunt momentele corespunzatoare rezistentelor la rulare la cele doua punti; Ra este rezistenta aerului; Rd reprezinta rezistenta la demarare; hg este inaltimea centrului de greutate, ha este inaltimea centrului de presiune unde actioneaza rezistenta aerului.
Tinanad seama de faptul ca:
Z1 + Z2 = Ga. cos α (9.3.)
rezulta:
Mr 1+ Mr 2= f.rd.Z1 + f.rd.Z2 = f.rd. ( Z1 + Z2 ) = f.rd.Ga.cosα ( 9.4.)
Reactiunile verticale Z1 si Z2 se obtin inlocuind relatiile 9.3 si 9.4 in relatiile 9.1 si 9.2:
![]() (9.5.)
(9.5.)
Z2 = ![]() (9.6.)
(9.6.)
Analizand ultimele doua relatii se poate constata ca marimea reactiunilor verticale la puntile automobilului depinde de marimea unghiului α de inclinare longitudinala a caii de rulare, de marimea rezistentei aerului Ra si de regimul de deplasare a automobilului ( prin rezistenta Rd). La cresterea vitezei de deplasare a automobilului, sau la cresterea unghiului α, se produce o descarcare dinamica a puntii fata (Z1 scade) si o supraincarcare dinamica a puntii din spate ( Z2 creste).
In cazul in care automobilul se deplaseaza cu viteza uniforma (dVa/dt=0),, rezistenta la demarare Rd se anuleaza, iar la viteze mici de deplasare rezistenta aerului Ra se poate neglija, ca avand valori nesemnificative, in raport cu celelalte rezistente. In aceste conditii relatiile 9.5 si 9.6 devin:
![]() (9.7)
(9.7)
Z2 = ![]() (9.8)
(9.8)
Daca automobilul se deplaseaza cu viteza uniforma pe drum orizontal, (α=0), relatiile, (.9.7.) si (9.8.) devin:
![]() (9.9)
(9.9)
Z2 = ![]() (9.10.)
(9.10.)
Pentru un automobil in repaus reactiunile normale ale caii asupra puntilor sunt influentate de repartitia statica pe punti a greutatii automobilului (cu si fara sarcina), de pozitia centrului de greutate si de inclinarea longitudinala α a drumului, figura 9.1. Aceste reactiuni se determina, asemanator cazului anterior, din ecuatiile de momente fata de punctele A si B :
G1 = Ga.![]() ; G2=Ga
; G2=Ga![]() (9.11.)
(9.11.)
Pe o cale orizontala (α=0) relatiile 9.7. devin:
G1 = Ga ![]() G2= Ga
G2= Ga ![]() (9.1)
(9.1)
in care : G1 si G2 sunt reactiunile statice la puntea din fata, respectiv la puntea din spate; Ga este greutatea totala a automobilului; a,b reprezinta distantele centrului de greutate fata de puntea fata, respectiv spate; L este ampatamentul; hg reprezinta inaltimea centrului de greutate.
Pentru determinarea valorilor maxime ale reactiunilor verticale dinamice, la limita aderentei rotilor cu calea de rulare, se scrie ecuatia de momente, figura 9.1., in raport cu centrul de greutate cg al automobilului:
Z1.a - Z2. b + Mr 1+Mr 2+ X2.hg+ Ra .(ha -hg) -X1 .hg=0 (9.13.)
in care: X1 = f . Z1 si X 2 = φ . Z2 reprezinta forta de aderenta (reactiunea tangentiala maxima).
Cu aceasta observatie, revenind la relatia (9.13.) si tinand seama de ecuatiile 9.3. si 9.4. rezulta:
Z1 =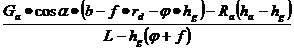 (9.14)
(9.14)
Z2 =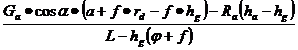 (9.15)
(9.15)
Daca se tine seama ca la deplasarea pe rampa, la limita aderentei, automobilul are viteza redusa, rezistenta aerului Ra se poate neglija. De asemenea valorile termenilor f . rd si f . hg , se pot neglija, ca fiind reduse in comparatie cu ceilalti termeni. Asadar se obtin expresiile:
Z1 =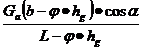 Z2=
Z2=![]() (9.16)
(9.16)
Cunoscand valoarea reactiunii verticale dinamice la puntea din spate, Z2, se poate determina forta de tractiune la limita aderentei cu relatia Xmax=φ.Z2, sau:
X2 =
φ. Z2 = φ . ![]() (9.17)
(9.17)
Pentru a vedea mai bine distribuirea greutatii intre puntile automobilului se obisnuieste ca reactiunile verticale dinamice sa se exprime in functie de incarcarile statice ale puntilor, cu ajutorul coeficientilor de incarcare dinamica mi , definiti ca fiind:
m1 = ![]() m2 =
m2 =![]() (9.18)
(9.18)
in care: m1, m2 sunt coeficientii de incarcare dinamica a puntilor din fata si spate.
Daca in relatiile 9.18. se inlocuiesc valorile fortelor Z1, Z2, G1, G2 cu valorile date de relatiile 9.1 si 9.16. rezulta:
m1=![]() m2=
m2= (9.19)
(9.19)
Din analiza relatiilor (9.19.) se constata ca m1 < 1 si m2 > 1, ceea ce arata ca in timpul deplasarii automobilului, avand puntea motoare in spate, apare o descarcare dinamica a puntii fata si o supraincarcare dinamica a puntii din spate, comparativ cu incarcarile lor statice.
Pentru automobilele care au ampatamentul L= 2,5-4,5 m, la deplasare pe cai orizontale, cu aderenta buna, puntea spate se supraincarca dinamic cu 10-30 % mai mult decat in conditii statice.
Fortele si momentele care actioneaza asupra automobilului avand puntea motoare in fata sunt reprezentate in figura 9. Reactiunea tangentiala la puntea din fata X1 este egala cu forta de tractiune si asigura propulsarea automobilului pe rampa, iar reactiunea tangentiala la puntea spate X2 este o forta indreptata in sens invers sensului de inaintare, fiind egala cu rezistenta la rulare:
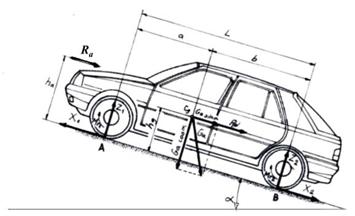
X1= φ.Z1: X2 = f. Z2 (9.20)
Fig.9. Automobil cu puntea motoare in fata
Scriind ecuatiile de momente in raport cu punctele A si B si tinand seama de relatia 9.20. rezulta expresiile reactiunilor verticale la cele doua punti:
Z1=![]() Z2 =
Z2 = 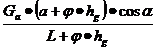 (9.21)
(9.21)
Cunoscand valoarea reactiunii verticale dinamice la puntea din fata, Z1, se poate determina forta de tractiune a automobilului avand puntea motoare in fata cu relatia Xmax= φ . Z1, adica:
Xmax=
φ . ![]() . (9.22)
. (9.22)
Coeficientii de incarcare dinamica a reactiunilor la puntea motoare fata m1, respectiv la puntea spate m2 ,se vor calcula cu relatiile:
m1=
![]() ; m2=
; m2= 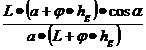 (9.23)
(9.23)
Analizand relatiile 9.23. se observa ca m1<1 si m2 > 1, ceea ce arata ca si in acest caz apare descarcarea dinamica a puntii fata si supraincarcarea puntii spate, comparativ cu sarcinile statice care revin puntilor, asemanator ca in cazul automobilului cu puntea motoare in spate.
Pentru cele mai multe automobile cu puntea motoare in fata, in conditii normale de deplasare m1= 0,8 - 0,9, ceea ce arata ca puntea spate se incarca suplimentar cu circa 10-20%, comparativ cu incarcarea sa statica .
Pentru un automobil avand ambele punti motoare fortele, momentele si reactiunile care actioneaza asupra sa sunt cele prezentate in figura 9.3.
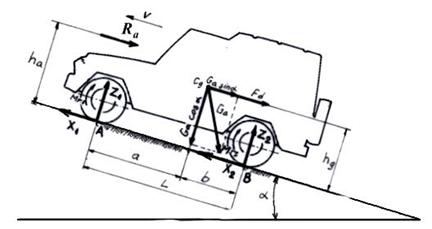
Fig.9.3.Automobil cu ambele punti motoare
Reactiunile tangentiale la ambele punti sunt forte de tractiune, orientate in sensul de deplasare ale automobilului si se calculeaza cu relatiile:
X1 = φ . Z1 si X2 = φ . Z2 (9.24)
Reactiunile normale la cele doua punti motoare se calculeaza asemanator cazurilor anterioare cu ajutorul expresiilor:
Z1
= ![]() Z2 =
Z2 =![]() (9.25)
(9.25)
iar coeficientii de schimbare dinamica a reactiunilor se calculeaza cu relatiile:
m1= ![]() m2 =
m2 = ![]() (9.26)
(9.26)
Pentru automobilul cu ambele punti motoare, de asemenea m1< 1 si m2 > 1, iar valorile lor uzuale sunt: m1 = 0,4-0,8 si m2 = 1,2-1,6 ceea ce inseamna ca schimbarea dinamica a reactiunilor normale in acest caz se face mult mai intens decat la automobilul cu o singura punte motoare.
Forta de tractiune maxima se determina dubland valoarea fortei de tractiune de la puntea la care reactiunea normala este mai mica:
-daca Z1< Z2 atunci Xmax= 2 . Z1 . φ ; (9.27.)
--daca Z2< Z1 atunci Xmax= 2 . Z2 . φ (9.28.)
In cazul mai rar in care reactiunile normale la cele doua punti sunt egale, Z1 = Z2 , forta de aderenta totala a automobilului se determina cu relatia:
Xmax =X1 max + X2 max = φ . (Z1 + Z2 ) = Ga . φ . cosα (9.29.)
![]()
1.Care sunt cauzele fizice ale aparitiei rezistentei la rulare ?
Care sunt cauzele fizice ale aparitiei rezistentei aerului?
Care sunt cauzele fizice ale aparitiei rezistentei la demarare ?
4.Ce valoare are momentul la roata MR fata de momentul efectiv Me al motorului?
a) mai mare;
b) mai mica;
c) egala.
5.Ce este forta de tractiune si unde actioneaza ea ?
6.Ce reprezinta bilantul de putere al automobilului?
7. Cum se defineste aderenta dintre pneu si calea de rulare?
8.Ce reprezinta cercul aderentei ? Dar elipsa de aderenta?
9.Explicati relatia existenta intre coeficientii m1 , m2 , de schimbare dinamica a reactiunilor la puntile automobilului
10. La ce este util calculul reactiunilor normale la punti ?

|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |