
Campul magnetic creat de o spira patrata
Campul magnetic pe axa Oz a unei spire patrata, de latura a, plasat in planul Oxy (Fig. 7.3) se deduce prin adunare vectoriala a campului creat de fiecare din laturi:
![]()
Componentele perpendiculare pe axa se compenseaza doua cate doua intre laturile opuse. In consecinta:
![]()
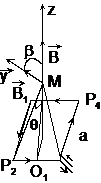
Figura 7.3
Cum B1 poate fi dedus facand ![]() , se obtine:
, se obtine:
![]()
unde
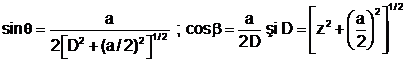
In final expresia campului magnetic devine:
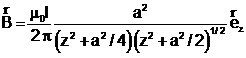 (7.13)
(7.13)
In centrul spirei se obtine:
![]() (7.14)
(7.14)
Calculul precedent poate fi extins cu usurinta pentru un poligon regulat cu N laturi. In acest caz se obtine:
![]() (7.15)
(7.15)
Din relatia (7.15) se poate deduce usor valoarea campului magnetic in centrul poligonului regulat:
![]() (7.16)
(7.16)
Prin trecere la limita in relatia (7.16) se poate obtine expresia campului magnetic in centrul unei spire circulare. In conditiile in care numarul de laturi N tinde la infinit, D va tinde spre R (raza cercului circumscris poligonului regulat) si se obtine:
![]() (7.17)
(7.17)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |