
Harti Karnaugh, tabele de adevar si expresii booleene
Hartile Karnaugh simplifica functiile logice mult mai rapid si mai usor in comparatie cu algebra booleana. Dorim simplificarea circuitelor logice spre cel mai mic cost posibil prin eliminarea componentelor. Definim cel mai mic cost ca fiind cel mai mic numar de porti cu cel mai mic numar de intrari pe poarta.
Mai jos am reprezentat cinci metode diferite de reprezentare a aceluiasi lucru: o functie logica aleatoare cu doua intrari. Metodele sunt: logica ladder, porti logice, tabel de adevar, harta Karnaugh si ecuatie booleana. Ceea ce vrem sa subliniem este ca toate acestea sunt echivalente. Doua intrari A si B pot lua valori de 0 sau 1, inalt sau jos, deschis sau inchis, adevarat sau fals, in functie de caz. Exista 22 = 4 combinatii pentru generarea unei iesiri. Acest lucru se aplica tuturor celor cinci exemple.
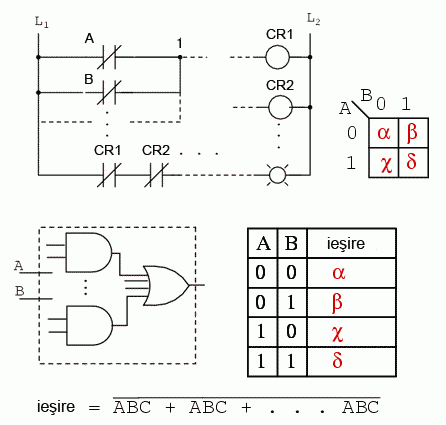
Aceste patru iesiri pot fi observate prin intermediul unei lampi la iesirea circuitului ce utilizeaza logica ladder. Aceste iesiri pot fi inregistrate intr-un tabel de adevar sau intr-o harta Karnaugh. Priviti harta Karnaugh ca si un tabel de adevar "cosmetizat". Iesirea ecuatiei booleene poate fi obtinuta cu ajutorul legilor algebrei booleene si transferata tabelului de adevar sau hartii Karnaugh. Care din cele cinci metode echivalente de reprezentare ar trebui sa o folosim? Cea mai folositoare pentru situatia in cauza.
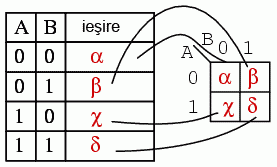
Iesirile unui tabel de adevar corespund unu-la-unu elementelor unei harti Karnaugh. Incepand cu partea de sus a tabelului de adevar, intrarile A = 0 si B = 0 produc iesirea α. Observati ca aceiasi iesire, α, se regaseste pe harta Karnaugh la adresa A = 0, B = 0, in partea de sus stanga, la intersectia coloanei B = 0 cu randul A = 0. Celelalte iesiri ale tabelului de adevar, β χ respectiv δ, corespunzatoare intrarilor AB = 01, 10 respectiv 11 au de asemenea corespondent pe harta Karnaugh:
Pentru usurinta expunerii, prezentam mai jos regiunile adiacente ale hartii Karnaugh cu doua variabile folosind metoda dreptunghiulara a diagramei Venn din sectiunea precedenta:
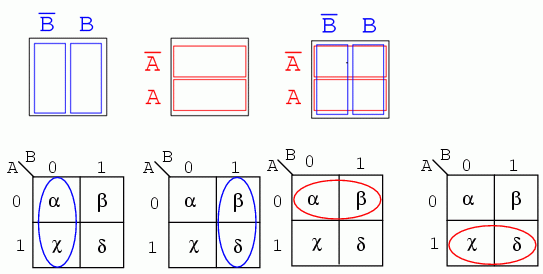
Regiunile α si χ sunt adiacente pe harta Karnaugh. Nu putem spune acelasi lucru despre tabelul de adevar precedent, intrucat exista o alta valoare (β) intre ele. Acesta este si motivul organizarii hartilor Karnaugh sub forma de matrice patrata. Regiunile cu variabile booleene comune trebuie sa se afla una langa cealalta. Aceasta structura este si trebuie sa fie usor de recunoscut cand privim o astfel de harta, din moment ce α si χ au variabila B' in comun. Stim acest lucru deoarece B este 0 (identic cu B') pentru coloana de deasupra celor doua regiuni. Comparati acest lucru cu diagrama Venn de deasupra hartii Karnaugh.
In aceiasi ordine de idei, putem observa ca β si δ au ca si variabila comuna B (B = 1). Prin urmare, α si β au in comun variabila booleana A' (A = 0), iar χ si δ variabila A (A = 1).
Pe scurt, am incercat sa grupam variabilele booleene pe regiuni astfel incat sa reiasa elementele lor comune. Hartile Karnaugh sunt organizate pentru a ne oferi exact aceasta "imagine".
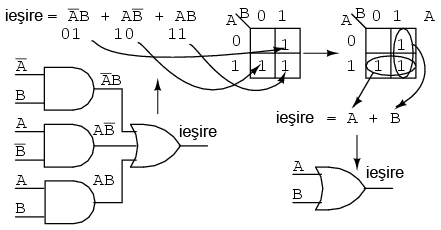
Tabelul de adevar de mai jos contine doua valori de 1. Harta Karnaugh trebuie sa contina si ea tot doua valori de 1:
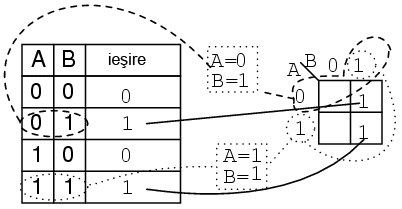
Sa incercam sa scriem acum pentru harta Karnaugh de mai sus si expresia booleana. Solutia este prezentata mai jos:
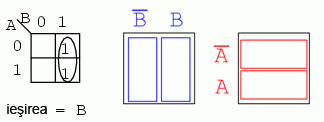
Acest lucru poate fi observat mai usor comparand diagramele Venn din dreapta, in mod special coloana B.
Scrieti expresia booleana asociata hartii Karnaugh de mai jos:
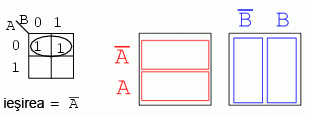
Urmand o logica asemanatoare celei de mai sus, grupam toate valorile de 1 si gasim variabila comuna intregului grup astfel format; rezultatul este A'.
Pentru tabelul de adevar de mai jos, gasiti harta Karnaugh corespunzatoare si scrieti apoi expresia booleana folosind rezultatul obtinut. Solutia este prezentata mai jos:
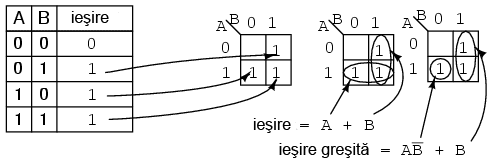
Solutia din mijloc este cea mai simpla si prezinta cel mai mic cost. O solutie mai putin dorita este cea din dreapta. Dupa gruparea valorilor 1, facem greseala de a forma un grup cu o singura regiune. Motivul pentru care acest lucru nu este de dorit este urmatorul: acest grup ce contine o singura regiune are termenul produsului egal cu AB'; solutia intregii hartii este in acest caz AB' + B, iar aceasta nu reprezinta cea mai simpla solutie.
Metoda corecta consta in gruparea acestui 1 singur cu regiunea din dreapta lui, regiune ce contine la randul ei o valoare de 1, chiar daca aceasta a fost deja inclusa intr-un alt grup. (coloana B). Putem refolosi regiuni pentru a forma grupuri mai mari. De fapt, este chiar indicat sa facem acest lucru intrucat conduce la rezultate mai simple.
Trebuie sa facem observatia ca oricare dintre solutiile de mai sus, atat cea corecta cat si cea "gresita" sunt de fapt corecte din punct de vedere logic. Ambele circuite vor genera aceiasi iesire. Pur si simplu, circuitul corect presupune un cost mai redus de implementare fizica.
Completati o harta Karnaugh folosind expresia booleana de mai jos. Scrieti apoi expresia booleana a rezultatului:
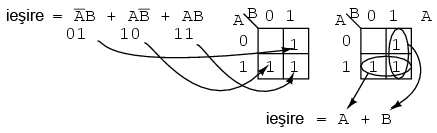
Expresia booleana contine trei sume de produse. Va exista cate o valoare de 1 pe harta Karnaugh pentru fiecare produs. Desi, in general, numarul valorilor de 1 pe produs variaza cu numarul variabilelor produsului in comparatie cu marimea hartii Karnaugh. Termenul produsului reprezinta adresa regiunii unde vom introduce valoare de 1. Primul termen este A'B si corespunde adresei 01 a hartii. Introducem un 1 in aceasta regiune. Similar, introducem si ceilalti doi termeni de 1.
Trecem apoi la gruparea termenilor si simplificarea rezultatului conform exemplului precedent.
Simplificati circuitul logic de mai jos:
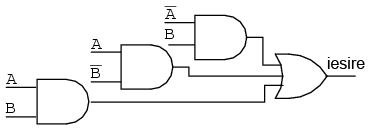
Simplificati circuitul logic de mai jos:
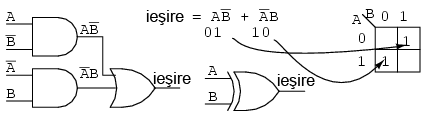
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |